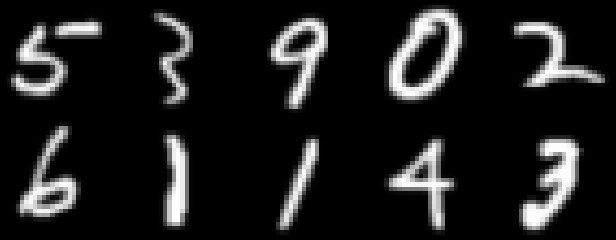Fractal Flow: Hierarchical and Interpretable Normalizing Flow via Topic Modeling and Recursive Strategy (2508.19750v1)

Abstract: Normalizing Flows provide a principled framework for high-dimensional density estimation and generative modeling by constructing invertible transformations with tractable Jacobian determinants. We propose Fractal Flow, a novel normalizing flow architecture that enhances both expressiveness and interpretability through two key innovations. First, we integrate Kolmogorov-Arnold Networks and incorporate Latent Dirichlet Allocation into normalizing flows to construct a structured, interpretable latent space and model hierarchical semantic clusters. Second, inspired by Fractal Generative Models, we introduce a recursive modular design into normalizing flows to improve transformation interpretability and estimation accuracy. Experiments on MNIST, FashionMNIST, CIFAR-10, and geophysical data demonstrate that the Fractal Flow achieves latent clustering, controllable generation, and superior estimation accuracy.

• The paper introduces Fractal Flow, a novel normalizing flow that leverages structured latent priors and recursive fractal design to enhance interpretability and density estimation.
• It integrates Kolmogorov–Arnold Networks with LDA-based topic modeling to achieve hierarchical latent space clustering and controllable sample generation.
• Empirical evaluations on MNIST, FashionMNIST, and CIFAR-10 demonstrate faster convergence and lower NLL while yielding semantically interpretable clusters.

Fractal Flow: Hierarchical and Interpretable Normalizing Flow via Topic Modeling and Recursive Strategy

Introduction and Motivation

The paper introduces Fractal Flow, a novel normalizing flow (NF) architecture designed to address the limitations of conventional flow-based generative models in terms of expressiveness and interpretability. Traditional NFs, while providing exact likelihood estimation and efficient sampling, often rely on simple latent priors (e.g., isotropic Gaussian) and monolithic transformation architectures, which restrict their ability to capture hierarchical or clustered data structures. The proposed approach leverages Kolmogorov–Arnold Networks (KANs), Latent Dirichlet Allocation (LDA), and a recursive fractal design to construct structured, interpretable latent spaces and hierarchical transformation modules.

Structured Latent Priors and KAT-based Normalizing Flows

Fractal Flow departs from the standard Gaussian prior by introducing structured latent priors inspired by the Kolmogorov–Arnold representation theorem (KAT). The KAT provides a theoretical foundation for expressing multivariate functions as compositions of univariate functions, which is operationalized in the model via KANs. KANs replace fixed nonlinear activations with learnable, grid-based B-spline functions on edges, enabling flexible and interpretable transformations.

The latent space is modeled as a mixture of Gaussians, where each component corresponds to a mode or cluster, and the transformation $T(\mathbf{x})$ is parameterized by deep invertible networks (e.g., RealNVP-style affine coupling layers). To preserve the structural consistency between the data and latent spaces, an $L_2$ regularization term penalizes excessive distortion during transformation.

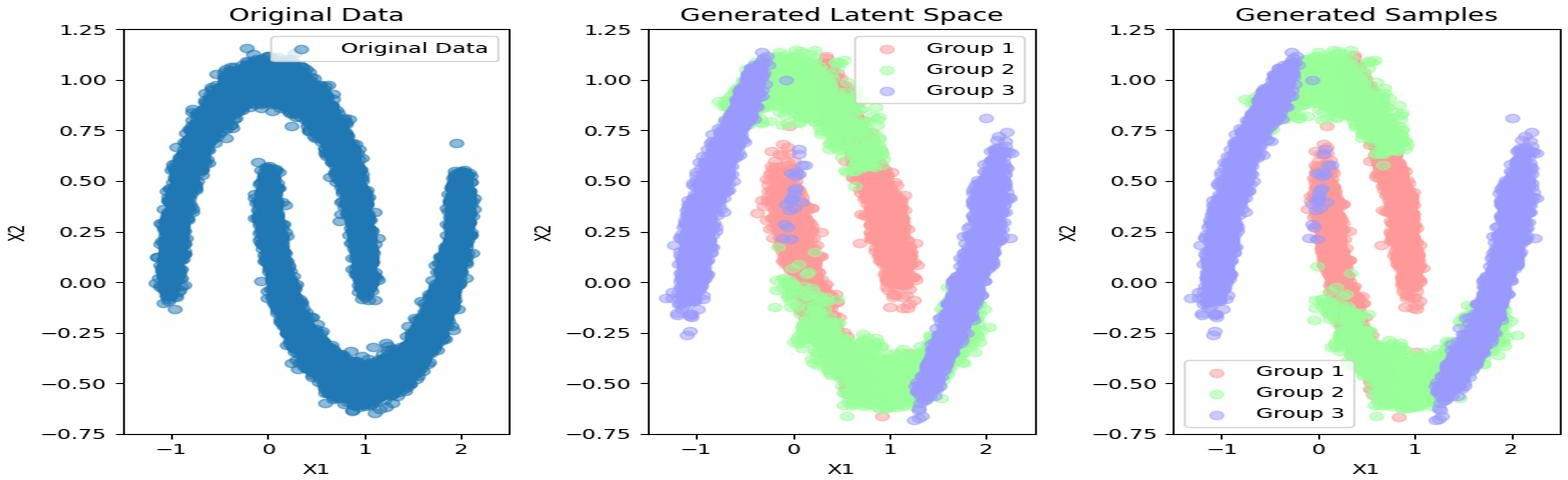
Figure 1: Visualization of a structured latent space using the Structured Latent Priors. The model effectively captures the underlying structure of the data.

The independence assumption in the latent space, justified by the additive structure of KAT, reduces computational complexity and aligns with the goal of disentangled representations.

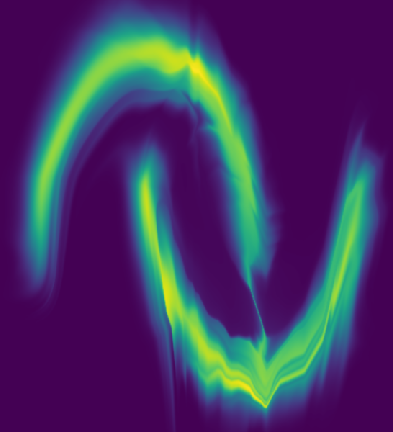
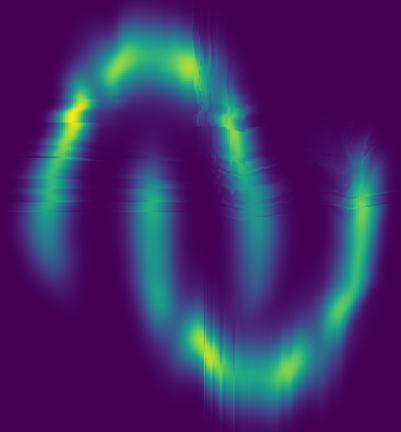
Figure 2: From left to right: RealNVP-based latent space, RealNVP-based MOON’s probability, KAT-based latent space, and KAT-based MOON’s probability.

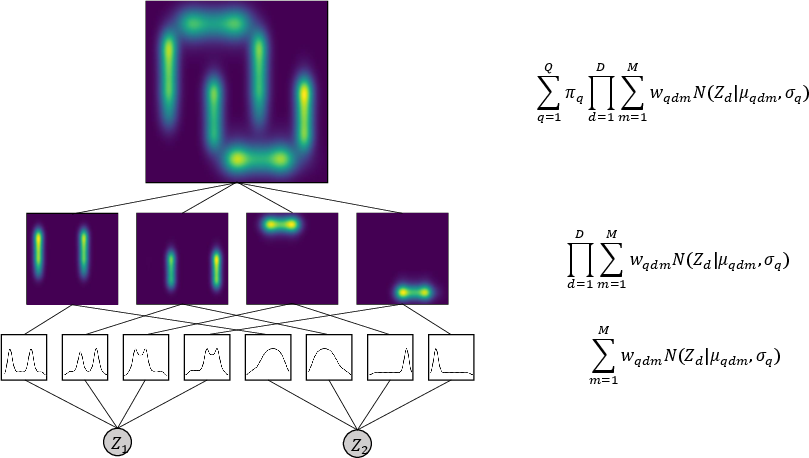
Figure 3: Neural network implementation of the structured latent space in a KAT-based normalizing flow model.

Latent Dirichlet Allocation for Hierarchical Topic Modeling

To further enhance interpretability and prevent mode collapse, the model incorporates LDA for probabilistic topic modeling over the grid-based Gaussian components in the latent space. LDA introduces Dirichlet priors over mixture weights, enabling hierarchical Bayesian modeling of latent topics and promoting diversity in generated samples. The two-level LDA mechanism assigns variance parameters at the top level and mean parameters conditioned on the first layer, resulting in a structured, interpretable latent space.

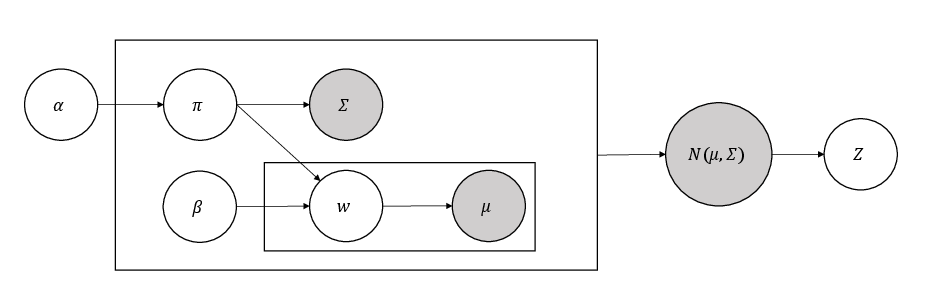
Figure 4: Statistical LDA-based modeling of the structured latent space. The latent space is constructed via a two-level LDA mechanism.

This approach allows the model to uncover semantic clusters and fine-grained styles in an unsupervised manner, as demonstrated in the qualitative experiments.

Fractal Coupling Layers and Recursive Architecture

The recursive fractal design is inspired by Fractal Generative Models (FGMs), where each invertible transformation step in the NF is treated as a module that can be recursively decomposed. After each transformation, the latent space is partitioned into blocks, each modeled by a smaller-scale NF, continuing until near-independence is achieved. This hierarchical approach enables the model to capture both local and global structures efficiently, improving parameter efficiency and interpretability.

Affine coupling layers are used as the basic reversible transformation, with scale and shift functions parameterized by MLPs or CNNs. The fractal architecture leverages local transformation modules at different spatial resolutions, progressively refining the representation from local details to global structure.

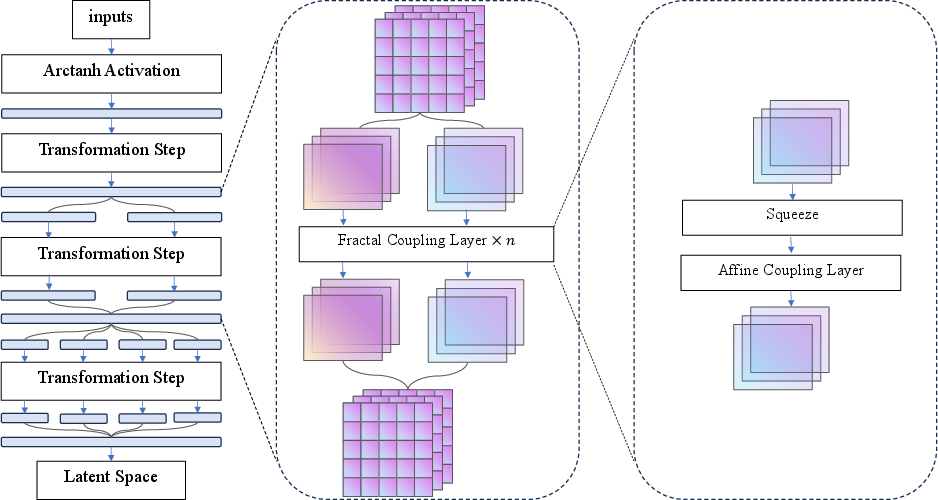
Figure 5: Network architecture of Fractal Generative Model based on affine coupling layers.

Experimental Results

Quantitative Evaluation

Experiments on MNIST, FashionMNIST, and CIFAR-10 (automobile class) demonstrate that the introduction of LDA layers and fractal coupling layers does not degrade negative log-likelihood (NLL) performance. In fact, the fractal architecture achieves lower NLL and faster convergence, with convolutional subnetworks yielding the best results. For MNIST, the LDAFNF (CNN) variant achieves 1.20 bits/dim, outperforming RealNVP (1.77 bits/dim).

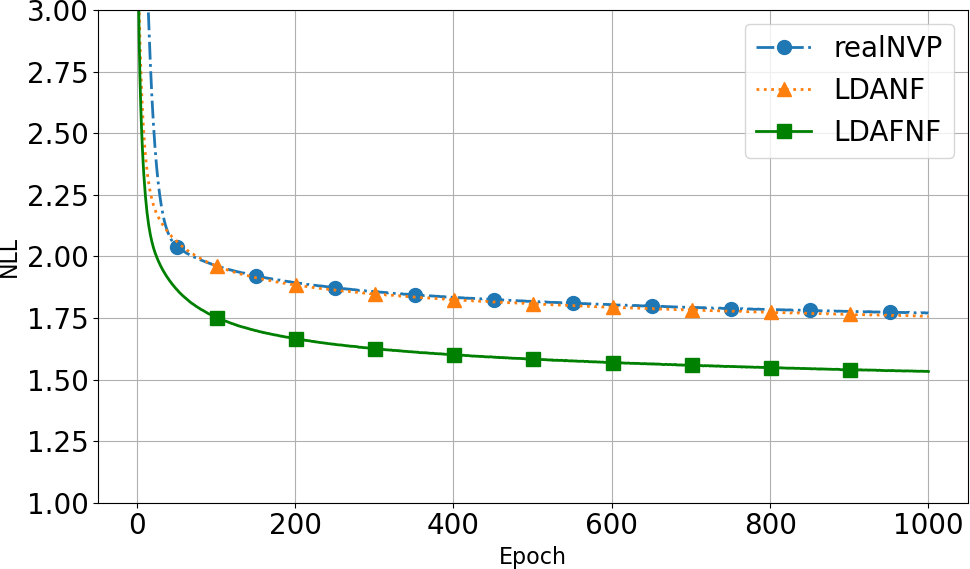
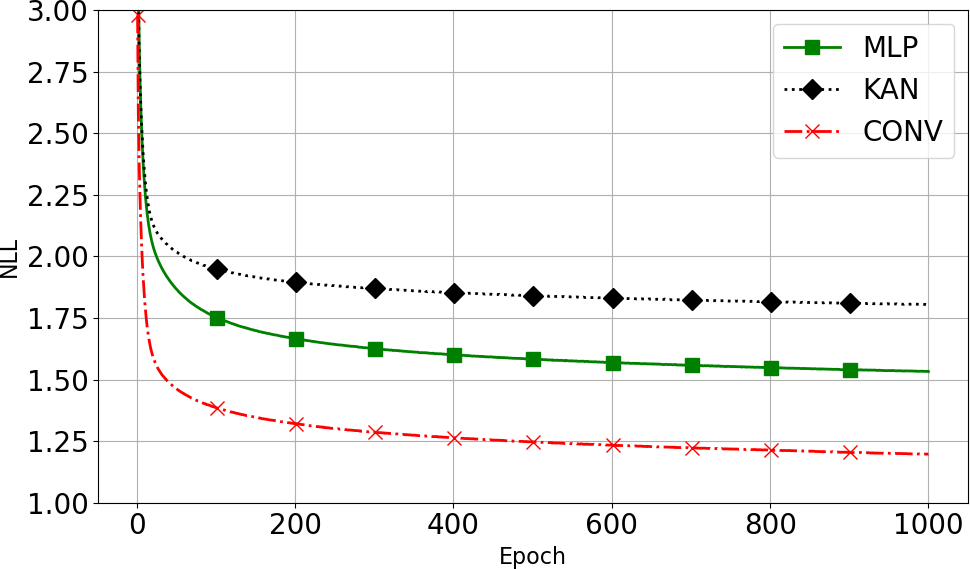
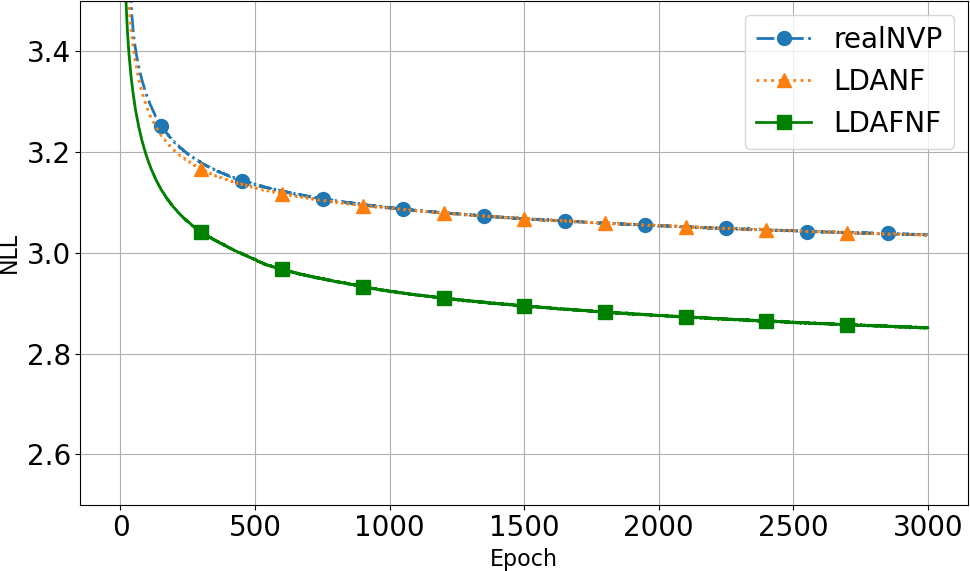
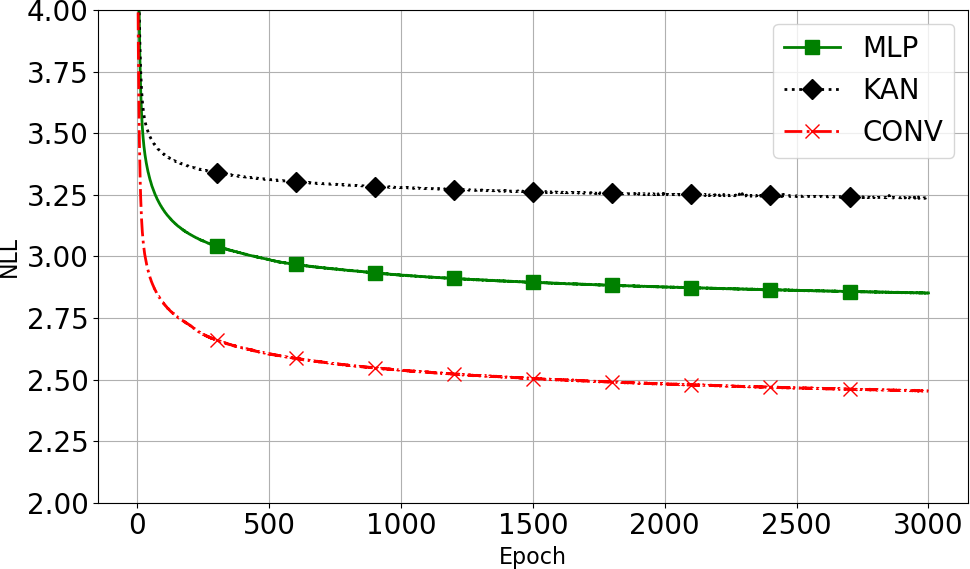
Figure 6: Ablation paper of the LDA layer and fractal coupling layer, along with comparisons of different subnetwork variants on MNIST and FashionMNIST.

Qualitative Evaluation

The model generates high-quality samples on MNIST, FashionMNIST, CIFAR-10, and seismic datasets. Manipulation of latent topics via LDA enables controllable generation and reveals interpretable semantic clusters, such as separating clothing and shoe categories in FashionMNIST.

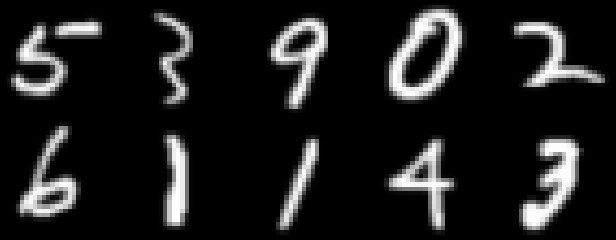
Figure 7: The top row shows samples from MNIST and FashionMNIST. The bottom row shows the random samples generated from the models.

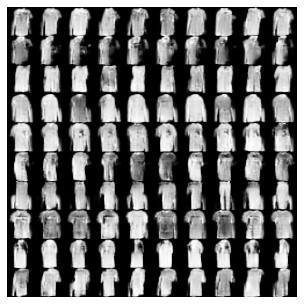
Figure 8: The top row shows random samples generated from two different covariance topics. The bottom row shows the random samples generated from different mean topics with each row corresponding to samples generated from the same mean.

Visualization of intermediate outputs at each fractal transformation step illustrates the progressive refinement of structure, from local to global patterns.

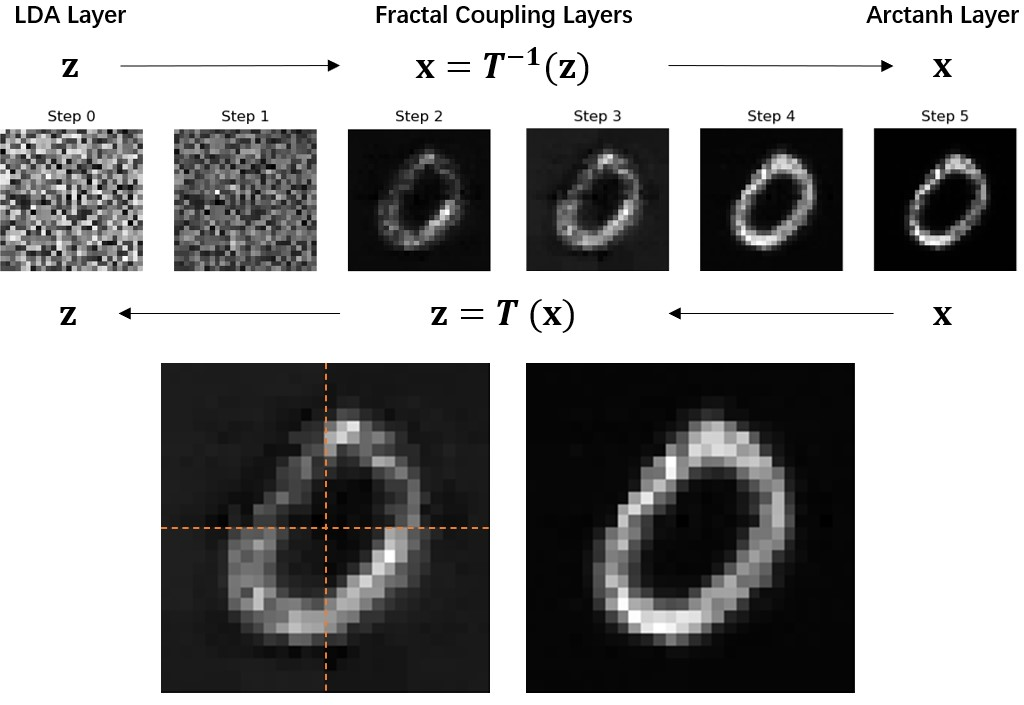
Figure 9: Visualization of the output at each transformation step on MNIST.

Figure 10: Visualization of the output at each transformation step on FashionMNIST.

The model also generalizes to more complex domains, generating recognizable automobile images and structurally coherent seismic signals.

Figure 11: Random samples generated on the automobile class of CIFAR-10.

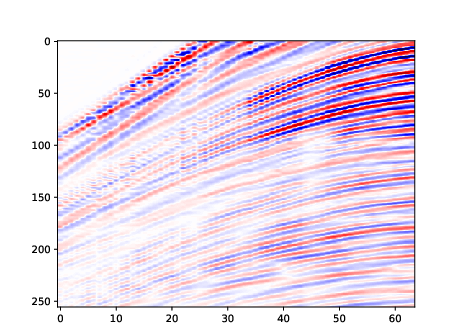
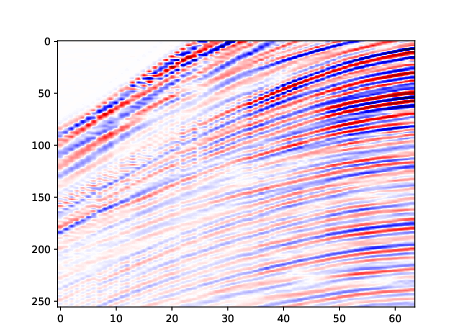
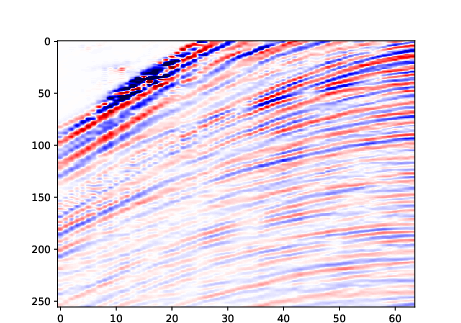
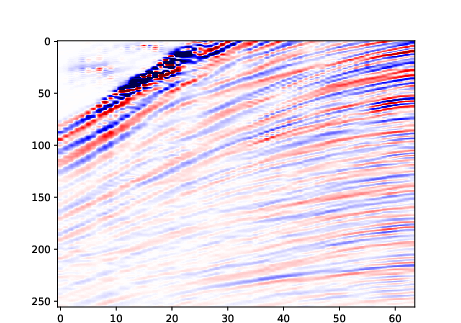
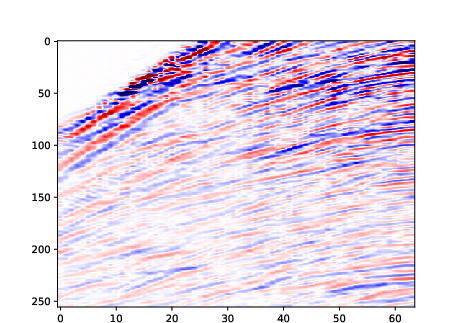
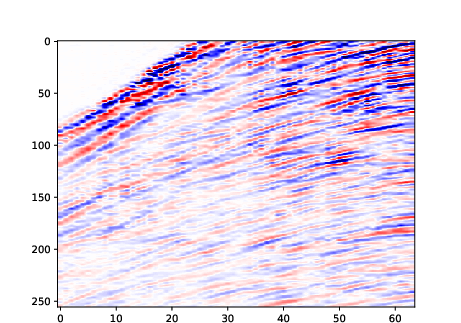
Figure 12: Random samples generated on the seismic dataset.

Implications and Future Directions

The integration of KANs, LDA, and fractal architectures in Fractal Flow advances the state of NF-based generative modeling by providing a principled framework for hierarchical, interpretable, and controllable latent space construction. The empirical results indicate that structured priors and recursive modularity can be incorporated without sacrificing density estimation performance, and in some cases, improve it.

Practically, the approach enables unsupervised discovery of semantic clusters, controllable sample generation, and applicability to domain-specific data (e.g., geophysical signals). Theoretically, the synergy between KAT, topic modeling, and fractal recursion opens avenues for further research in interpretable deep generative models.

Potential future developments include:

• Exploration of adaptive coupling architectures and tighter integration between latent priors and transformation modules.
• Enhancement of fractal flow via optimal transport theory for improved sample quality and interpretability.
• Hybridization with diffusion models to develop fractal flow-based diffusion frameworks.

Conclusion

Fractal Flow presents a hierarchical and interpretable normalizing flow architecture that leverages structured latent priors, topic modeling, and recursive fractal design. The model achieves competitive or superior density estimation, interpretable latent clustering, and controllable generation across diverse datasets. The proposed framework offers a promising direction for advancing both the theoretical understanding and practical deployment of interpretable deep generative models.