Magnetic reversals in a geodynamo model with a stably-stratified layer (2508.17777v1)

Abstract: We study the process of magnetic reversals in the presence of a stably-stratified layer below the core-mantle boundary using direct numerical simulations of the incompressible magnetohydrodynamics equations under the Boussinesq approximation in a spherical shell. We show that the dipolar-multipolar transition shifts to larger Rayleigh numbers in the presence of a stably-stratified layer, and that the dipolar strength of the magnetic field at the core-mantle boundary increases due to the skin effect. By imposing an heterogeneous heat flux at the outer boundary, we break the equatorial symmetry of the flow, and show that different heat flux patterns can trigger different dynamo solutions, such as hemispheric dynamos and polarity reversals. Using kinematic dynamo simulations, we show that the stably-stratified layer leads to similar growth rates of the dipole and quadrupole components of the magnetic field, playing the role of a conducting boundary layer, favouring magnetic reversals, and a dynamics predicted by low-dimensional models.

• The paper demonstrates that a stably-stratified layer amplifies the dipolar magnetic field via a skin effect, shifting the dipolar-multipolar transition.
• It employs direct numerical simulations of MHD equations in a spherical shell, varying SSL thickness and heterogeneous CMB heat flux patterns to break symmetry.
• The study finds that reduced differences in dipole and quadrupole growth rates enable robust, chaotic polarity reversals, offering insights into Earth-like magnetic behavior.

Magnetic Reversals in a Geodynamo Model with a Stably-Stratified Layer

Introduction and Motivation

This paper investigates the influence of a stably-stratified layer (SSL) beneath the core-mantle boundary (CMB) on the dynamics of planetary magnetic fields, with a particular focus on the mechanisms underlying magnetic polarity reversals. The geodynamo process, responsible for generating planetary magnetic fields, is governed by the interplay between convective motions, rotation, and magnetohydrodynamic (MHD) effects in the fluid outer core. Recent seismic and geomagnetic evidence suggests the existence of an SSL at the top of Earth's core, which may significantly affect the morphology and temporal evolution of the magnetic field. The paper employs direct numerical simulations (DNS) of the incompressible MHD equations under the Boussinesq approximation in a rotating spherical shell, systematically varying the SSL thickness and imposing heterogeneous heat flux patterns at the CMB to break equatorial symmetry.

Model Formulation and Numerical Methods

The system is modeled using the incompressible MHD equations in a spherical shell with aspect ratio $\chi = 0.35$, representative of Earth's core geometry. The SSL is introduced via a piecewise static temperature gradient, with a linear profile in the stably-stratified region and a solution to Laplace's equation in the convective region. The key control parameters are the Ekman number ($\Ek$), magnetic Prandtl number ($\Pm$), thermal Prandtl number ($\Pr$), and Rayleigh number ($\Ra$). Boundary conditions include no-slip velocity at both boundaries, fixed temperature at the inner boundary, and fixed heat flux at the CMB. The PARODY-JA code is used for DNS, employing pseudo-spectral methods in angular directions and finite differences radially, with parallelization via MPI and OpenMP.

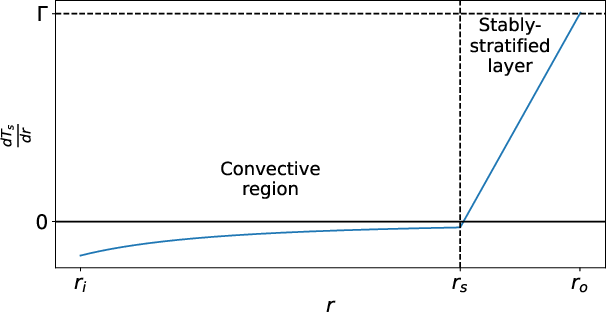
Figure 1: Schematic of the static temperature gradient, illustrating the convective region and the stably-stratified layer beneath the CMB.

Heterogeneous heat flux at the CMB is imposed using axisymmetric spherical harmonics ($Y_1^0$, $Y_3^0$, and their linear combinations), with the amplitude parameter $\delta q$ controlling the degree of symmetry breaking. The outputs of interest include the dipolar field strength at the CMB ($f_\mathrm{dip}$), the local Rossby number ($\Rol$), and the hemisphericity parameter ($\mathcal{H}_\mathrm{cmb}$).

Effects of the Stably-Stratified Layer on Dynamo Morphology

The presence of an SSL leads to a pronounced skin effect, attenuating high-order magnetic field modes and enhancing the dipolar component at the CMB. As the SSL thickness ($H_s$) increases, $f_\mathrm{dip}$ rises for fixed $\Ra/\Ra_c$, indicating a stronger, more Earth-like dipolar field. The dipolar-multipolar transition, typically controlled by $\Ra$ or $\Rol$, shifts to higher values and becomes more abrupt with increasing SSL thickness.

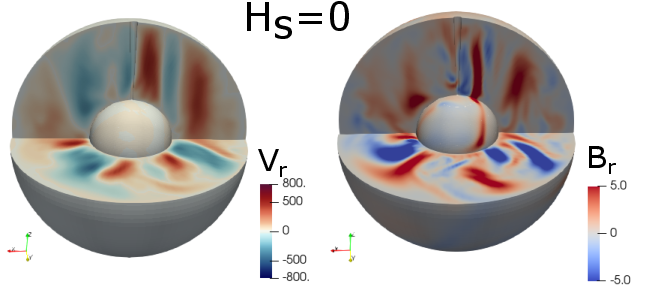
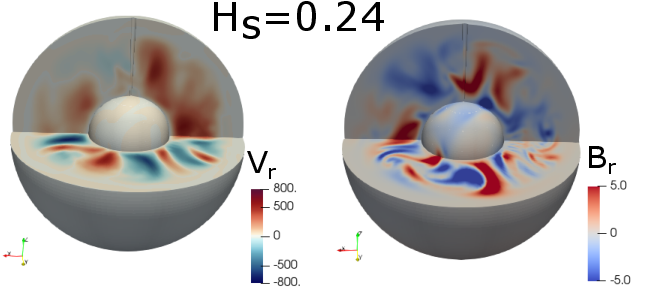
Figure 2: Time-averaged dipolar strength $f_\mathrm{dip}$ as a function of SSL thickness $H_s$ for various Rayleigh numbers, demonstrating the skin effect and field morphology changes.

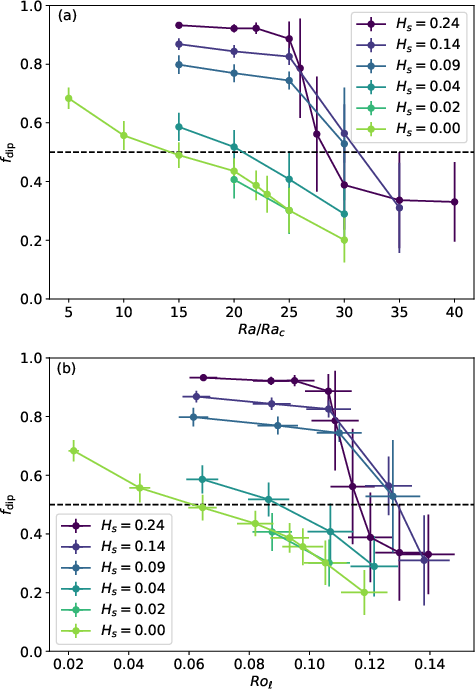
Figure 3: Dipolar-multipolar transition as a function of Rayleigh number and local Rossby number for different SSL thicknesses.

This result implies that the SSL acts as a low-pass filter, favoring large-scale, slowly varying magnetic field structures and suppressing small-scale, rapidly fluctuating modes.

Symmetry Breaking and Dynamo Regimes

Imposing heterogeneous heat flux at the CMB breaks equatorial symmetry and induces a range of dynamo regimes. For the $Y_1^0$ pattern, increasing $\delta q$ enhances the quadrupolar component and leads to hemispheric dynamos, characterized by strong hemisphericity in the magnetic field. The transition to hemisphericity occurs for modest symmetry breaking ($\delta q \sim 5\%$), with minimal impact on the overall kinetic energy.

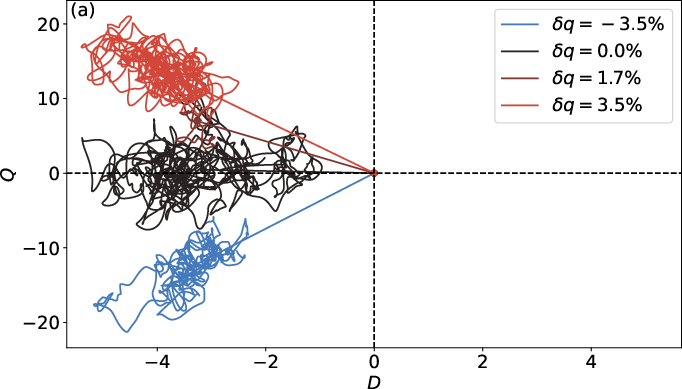
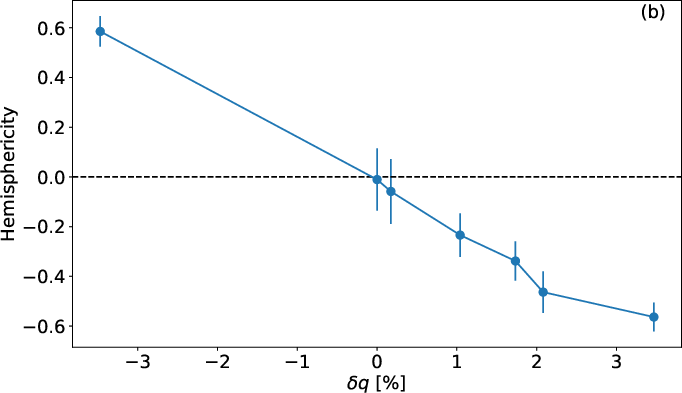
Figure 4: (a) Magnetic field evolution in dipole-quadrupole (D-Q) phase space for varying $\delta q$ ($Y_1^0$ pattern). (b) Time-averaged hemisphericity as a function of $\delta q$.

For the $Y_3^0$ pattern, the system exhibits polarity reversals, with the dipole component reversing first, followed by the quadrupole. The reversals are non-periodic and chaotic, with the dipolar strength dropping below $f_\mathrm{dip} < 0.5$ during reversal events.

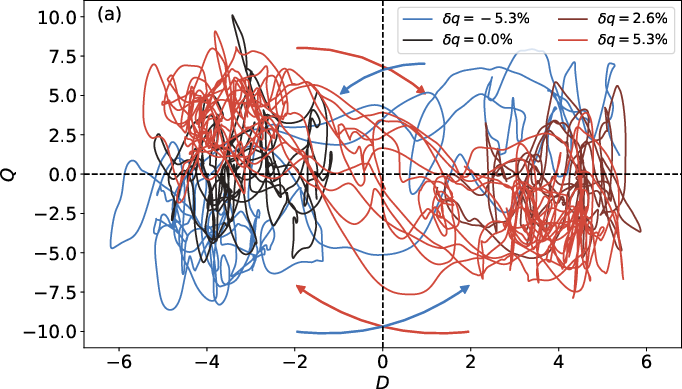
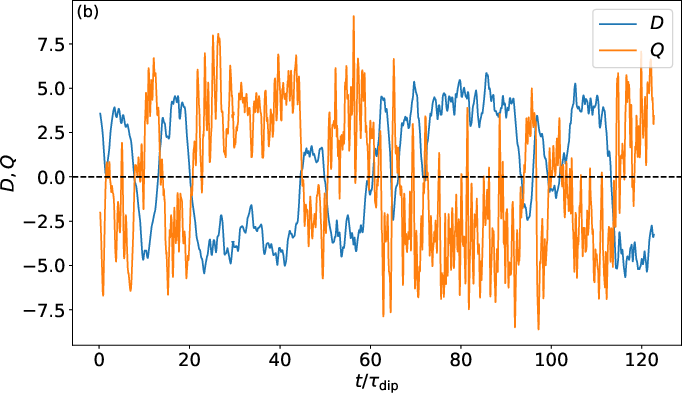
Figure 5: (a) D-Q phase space trajectories for $Y_3^0$ pattern and different $\delta q$. (b) Time series of dipole and quadrupole for $\delta q = 5.3\%$.

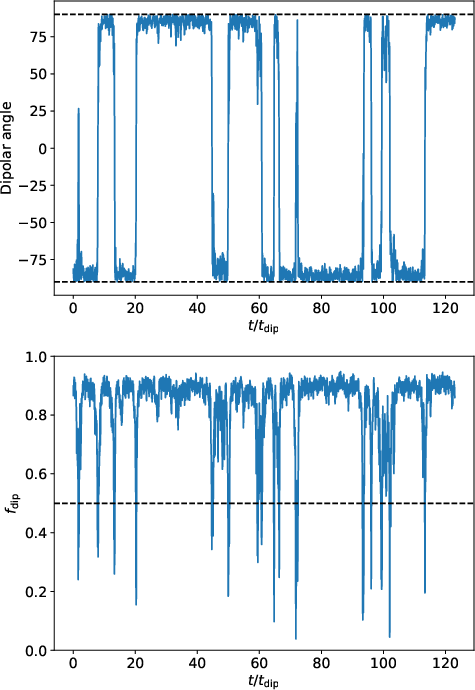
Figure 6: Time evolution of polarity reversals as a function of dipolar diffusion time for $Y_3^0$ symmetry breaking.

A linear combination of $Y_1^0$ and $Y_3^0$ patterns produces reversals with distinct trajectories in D-Q space, with a larger time delay between dipole and quadrupole reversals compared to the pure $Y_3^0$ case.

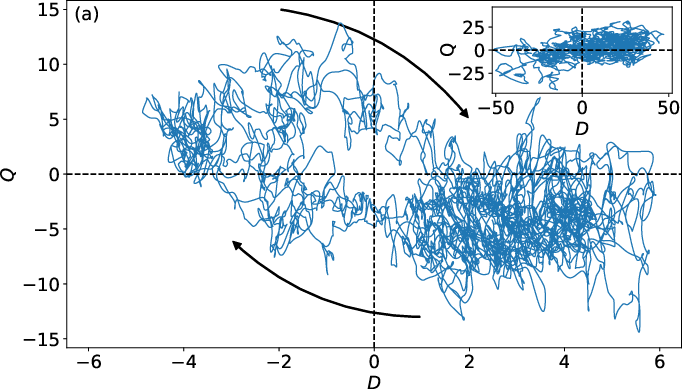
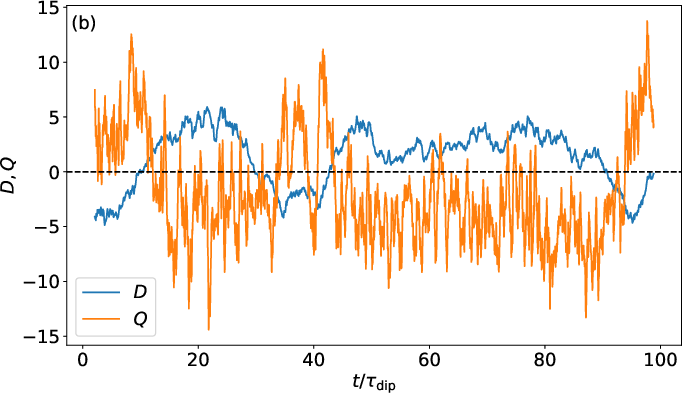
Figure 7: D-Q phase space evolution for combined $Y_1^0 + Y_3^0$ heat flux pattern, showing reversal trajectories and comparison to fully convective domain.

Low-Dimensional Interpretation and Kinematic Dynamo Analysis

The observed dynamical regimes are interpreted using low-dimensional models describing the nonlinear interaction between the axial dipole ($D$) and quadrupole ($Q$) components. The model equations include linear growth rates ($\sigma_D$, $\sigma_Q$), symmetry-breaking couplings, and cubic nonlinearities. When $\sigma_D \approx \sigma_Q$, symmetry breaking induces strong coupling, leading to either periodic reversals or hemispheric dynamos, consistent with the DNS results.

Kinematic dynamo simulations (Lorentz force removed) reveal that the SSL reduces the difference between dipole and quadrupole growth rates, approaching degeneracy as SSL thickness increases. This effect is analogous to the behavior predicted for $\alpha^2$-dynamos with perfectly conducting boundary layers.

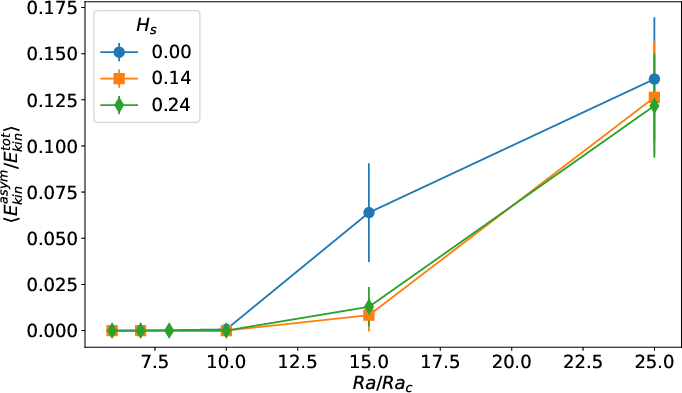
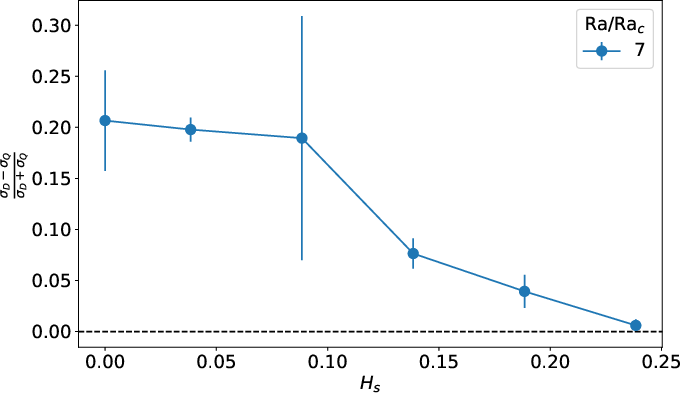
Figure 8: (a) Relative antisymmetric kinetic energy and (b) relative growth rate difference between dipole and quadrupole as a function of SSL thickness and Rayleigh number.

The SSL thus acts as an effective conducting boundary, stabilizing the dipole-quadrupole interaction and facilitating robust reversal dynamics even under weak symmetry breaking.

Implications and Future Directions

The results demonstrate that the SSL plays a critical role in shaping the geodynamo's reversal behavior. By enhancing the dipolar field and reducing the difference in growth rates between dipole and quadrupole modes, the SSL enables low-dimensional reversal dynamics to persist over a wide range of core conditions. This mechanism provides a plausible explanation for the observed robustness of Earth's magnetic reversals, despite significant variability in core properties over geological timescales.

The paper is conducted at $\Ek=10^{-3}$, which is orders of magnitude larger than Earth's value ($\Ek \sim 10^{-15}$). Future work should address the scaling of these phenomena with decreasing Ekman and magnetic Prandtl numbers, and explore the interplay between SSL properties and other core processes (e.g., compositional stratification, inner-core growth).

Conclusion

This work establishes the SSL beneath the CMB as a key factor in controlling the morphology and reversal dynamics of planetary magnetic fields. The SSL enhances the dipolar component via the skin effect, shifts the dipolar-multipolar transition, and enables robust reversal dynamics through near-degeneracy of dipole and quadrupole growth rates. The interplay between SSL thickness and heterogeneous heat flux patterns at the CMB produces a rich variety of dynamo regimes, including hemispheric dynamos and Earth-like polarity reversals. These findings have significant implications for understanding the long-term stability and variability of planetary magnetic fields, and motivate further investigation into the role of stratification and boundary conditions in geodynamo models.