Proof of a Generalized Ryu-Takayanagi Conjecture (2508.14877v1)

Abstract: We derive a generalized version of the Ryu-Takayanagi formula for the entanglement entropy in arbitrary diffeomorphism invariant field theories. We use a recent framework which expresses the measurable quantities of a quantum theory as a weighted sum over paths in the theory's phase space. If this framework is applied to a field theory on a spacetime foliated by a hypersurface $\Sigma,$ the choice of a codimension-2 surface $B$ without boundary contained in $\Sigma$ specifies a submanifold in the phase space. For diffeomorphism invariant field theories, a functional integral expression for their density matrices was recently given and then used to derive bounds on phase space volumes in the considered submanifold associated to $B.$ These bounds formalize the gravitational entropy bound. Here, we present an implication of this derivation in that we show the obtained functional integral expression for density matrices to be naturally suited for the replica trick. Correspondingly, we prove a functional integral expression for the associated entanglement entropies and derive a practical prescription for their evaluation to leading order and beyond. An important novelty of our approach is the contact to phase space. This allows us both to obtain a prescription for entanglement entropies in arbitrary diffeomorphism invariant field theories not necessarily possessing a holographic dual as well as to use entanglement entropies to study their phase space structure. In the case of the bulk-boundary correspondence, our prescription consistently reproduces and hence provides a natural and independent proof of the Ryu-Takayanagi formula as well as its various generalizations. These include the covariant holographic entanglement entropy proposal, Dong's proposal for higher-derivative gravity as well as the quantum extremal surface prescription.

• The paper introduces a formal proof of a generalized Ryu-Takayanagi conjecture using a phase space path integral method to compute entanglement entropy.
• It employs the replica trick combined with extremization procedures to derive gravitational entropy bounds and identify quantum extremal surfaces.
• The study broadens the applicability of entropic evaluations beyond holographic duals, impacting analyses in quantum gravity and field theories.

Proof of a Generalized Ryu-Takayanagi Conjecture

Introduction

The paper establishes a generalized version of the Ryu-Takayanagi formula to evaluate the entanglement entropy in diffeomorphism invariant field theories. Using a path integral approach in the phase space, the paper offers a novel prescription for entanglement entropy, not constrained to theories with holographic duals. This formal proof is significant as it extends prior hunches into rigorously derived results within quantum gravity.

Geometry of Possibilities

The research interprets quantum states as sums of possible evolutionary paths dictated by their geometrical properties, which defines the accuracy and resolve of measurable quantities in quantum mechanics. This "integral geometry" perspective allows a deeper exploration of quantum systems, including explanations for phenomena such as the limited state resolution in black holes (black hole entropy) and the mass gap in quantum chromodynamics (QCD).

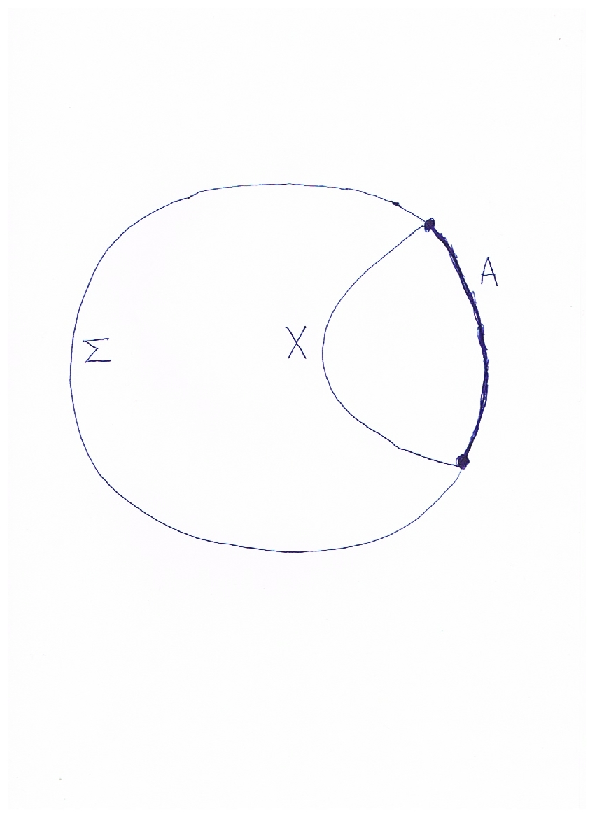
Figure 1: Sigma is represented by the disk with the circle being its boundary. The possifold flow is defined by the surface B= X \cup A. It bounds the region Sigma(B) between X and A.

Central to deriving entanglement entropies is the use of an integral geometry approach over phase space paths. Associating submanifolds in phase space with entanglements, the analysis yields gravitational entropy bounds and integrates easily into the replica trick for deeper analysis of such systems.

Derived Entanglement Entropy Formula

The heart of the paper is the functional integral expression for entanglement entropies, applicable universally to diffeomorphism invariant field theories. The reliance on phase space sum paths and the intrinsic covariance intrinsic to quantum states culminate in a formal expression for modular and, consequently, entanglement entropy:

$S = -\operatorname{tr} (\rho \ln (\rho))$

The formula hinges on the replica trick, leveraging integer powers of density matrices and analytic continuations, painting a picture of entanglement entropic behavior reflective of underlying quantum states. The contact with phase space, not present in former prescriptions, enables broad applicability beyond holographically interpreted theories.

Evaluation of Entanglement Entropy

The paper delineates a replicable methodology for computing this entropy, from exact expressions for $\rho^n$ to numerical approaches via perturbations. In particular, the method for approximating solutions involves iterative refinement akin to extremizing the generator $K$ of the diffeomorphism invariant field theory:

1. Construction of Initial Geometries:
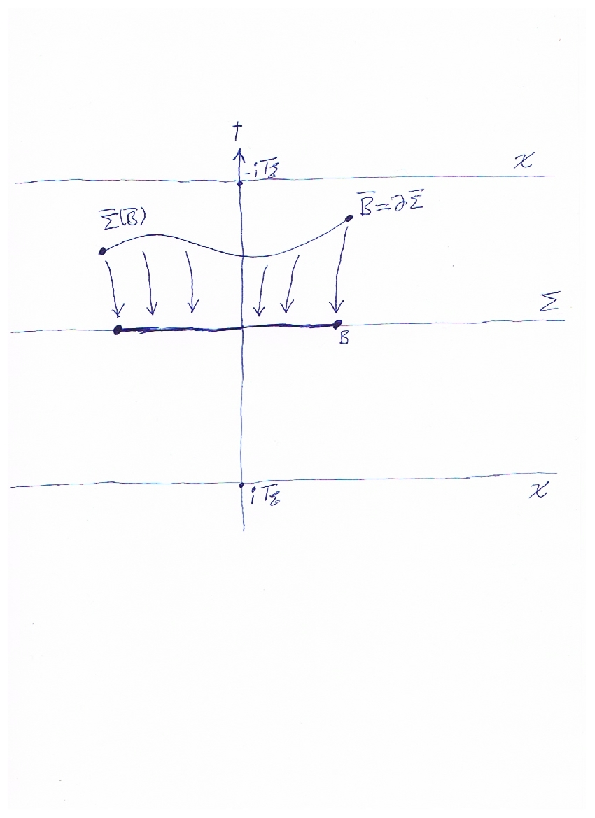
   • Foliation of spacetime with $\Sigma$, establishing the base for evolving solutions derived from field equations (Figure 1).
2. Replica Spacetime Translation:
   • Constructs a geometrically significant subsystem based on codimension-2 surface $B$, allowing deeper examination of entropic components as per given methodology.

     Figure 2: Visualization of the prescription to evaluate \eqref{33}.

3. Extremization Procedures:
   • Evaluation within classical limits to identify minimal action in spacetime evolvements, resulting in discernible quantum extremal surfaces.

Comparison with the Bulk-Boundary Correspondence

The methods align with Ryu-Takayanagi conjectures within bulk-boundary duality contexts, revealing the broader applicability and rigorous strengthening of its constituent equations. Augmenting the original prescription are adjustments regarding boundary deformations (Figure 1), enhancing traditional geometric understanding to boundary regions directly involved in spacetime evolutions.

Conclusion

This derivation confirms and broadens the Ryu-Takayanagi conjectures, illustrating universally applicable entropic evaluations in quantum field frameworks. By disentangling these aspects, the paper strengthens the geometric bridge across quantum entanglement and phase space dynamics., poised for further explorations in non-holographic settings and quantum cosmologies. These advancements foster additional inquiries into phase space dynamics as they pertain to the cumulative understanding of quantum gravitational systems.