Adaptively Robust LLM Inference Optimization under Prediction Uncertainty (2508.14544v1)

Abstract: We study the problem of optimizing LLM inference scheduling to minimize total latency. LLM inference is an online and multi-task service process and also heavily energy consuming by which a pre-trained LLM processes input requests and generates output tokens sequentially. Therefore, it is vital to improve its scheduling efficiency and reduce the power consumption while a great amount of prompt requests are arriving. A key challenge in LLM inference scheduling is that while the prompt length is known upon arrival, the output length, which critically impacts memory usage and processing time, is unknown. To address this uncertainty, we propose algorithms that leverage machine learning to predict output lengths, assuming the prediction provides an interval classification (min-max range) for each request. We first design a conservative algorithm, $\mathcal{A}{\max}$, which schedules requests based on the upper bound of predicted output lengths to prevent memory overflow. However, this approach is overly conservative: as prediction accuracy decreases, performance degrades significantly due to potential overestimation. To overcome this limitation, we propose $\mathcal{A}{\min}$, an adaptive algorithm that initially treats the predicted lower bound as the output length and dynamically refines this estimate during inferencing. We prove that $\mathcal{A}{\min}$ achieves a log-scale competitive ratio. Through numerical simulations, we demonstrate that $\mathcal{A}{\min}$ often performs nearly as well as the hindsight scheduler, highlighting both its efficiency and robustness in practical scenarios. Moreover, $\mathcal{A}_{\min}$ relies solely on the lower bound of the prediction interval--an advantageous design choice since upper bounds on output length are typically more challenging to predict accurately.

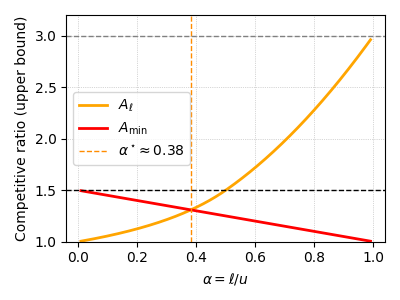
• The paper introduces an adaptive algorithm, A_min, that leverages lower-bound estimates to optimize LLM inference latency while adhering to GPU memory limits.
• It demonstrates that A_min achieves a competitive ratio of O(log(1/α)) and outperforms naive conservative methods, especially under wide prediction intervals.
• Empirical evaluations on the LMSYS-Chat-1M dataset show that A_min closely approximates hindsight-optimal performance even with significant output uncertainty.

Adaptively Robust LLM Inference Optimization under Prediction Uncertainty

Introduction and Problem Formulation

The paper addresses the problem of online scheduling for LLM inference under output length uncertainty, with the objective of minimizing total end-to-end latency subject to GPU memory (KV cache) constraints. In LLM serving, each request's prompt length is known at arrival, but the output length—directly impacting both memory usage and processing time—is unknown and must be predicted. The scheduling challenge is compounded by the need to batch requests efficiently while avoiding memory overflows and minimizing latency, especially as LLM inference is both compute- and energy-intensive.

The authors formalize the scheduling problem as a semi-online, resource-constrained batch scheduling task. Each request $i$ has a known prompt size $s$ and an unknown output length $o_i \in [\ell, u]$, where $[\ell, u]$ is a prediction interval provided by a machine learning model. The system processes requests in batches, with the total memory usage at any time $t$ constrained by the available KV cache $M$. The performance metric is the total end-to-end latency (TEL), defined as the sum of completion times for all requests.

Baseline and Naive Algorithms

The paper first reviews the hindsight-optimal algorithm (H-SF), which assumes perfect knowledge of all $o_i$ and greedily batches the shortest jobs first, achieving the minimum possible TEL. The competitive ratio (CR) is used to evaluate online algorithms relative to H-SF.

A naive conservative algorithm, $\mathcal{A}_{\max}$, is introduced, which pessimistically assumes every request has output length $u$ (the upper bound of the prediction interval). This approach guarantees no memory overflows but is highly conservative, leading to poor memory utilization and increased latency as the prediction interval widens. Theoretical analysis shows that the competitive ratio of $\mathcal{A}_{\max}$ is upper bounded by $\frac{\alpha^{-1}(1+\alpha^{-1})}{2}$ and lower bounded by $\frac{\alpha^{-1}(1+\alpha^{-1/2})}{2}$, where $\alpha = \ell/u$.

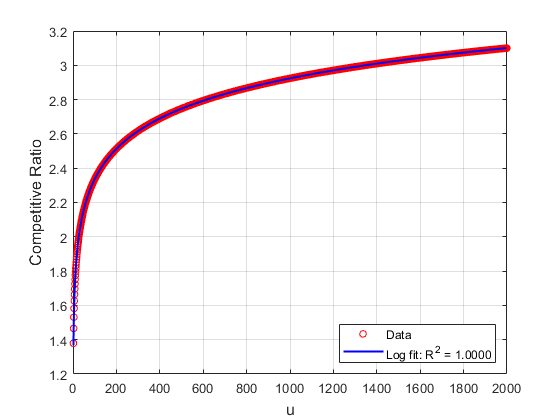
Figure 1: Competitive ratio of $\text{A}_{\min}$ as a function of the upper bound $u$, demonstrating logarithmic scaling with $u$.

Robust Adaptive Algorithm: $\mathcal{A}_{\min}$

To address the limitations of $\mathcal{A}_{\max}$, the authors propose $\mathcal{A}_{\min}$, an adaptive algorithm that leverages only the lower bound $\ell$ of the prediction interval. $\mathcal{A}_{\min}$ initializes each request's estimated output length to $\ell$ and dynamically refines this estimate as tokens are generated. If a memory overflow is imminent, the algorithm evicts jobs with the smallest accumulated lower bounds, updating their estimates accordingly. Batch formation is always based on the current lower bounds, and the algorithm never relies on the upper bound $u$.

Theoretical analysis establishes that $\mathcal{A}_{\min}$ achieves a competitive ratio of $\mathcal{O}(\log(\alpha^{-1}))$ as $M \to \infty$, a significant improvement over $\mathcal{A}_{\max}$, especially when prediction intervals are wide. The analysis leverages a Rayleigh quotient formulation and matrix spectral analysis to bound the competitive ratio logarithmically in $u$.

Distributional Extensions and Algorithm Selection

The paper further analyzes $\mathcal{A}_{\min}$ under specific output length distributions:

• Two-point distribution: For $o_i \in \{\ell, u\}$, $\mathcal{A}_{\min}$ achieves a competitive ratio $\leq 1.5$, while a specialized promote-$\ell$ policy $\mathcal{A}_\ell$ can further improve the bound to $1 + \frac{\alpha}{2(1-\alpha)}$ for $\alpha < 0.38$.
• Geometric and linearly weighted geometric distributions: Empirical and analytical results show that $\mathcal{A}_{\min}$'s competitive ratio is uniformly bounded by $1.7$ and $1.56$, respectively.

  Figure 2: Upper-bound curves for the competitive ratios under $\mathcal{D}_2$; $\mathcal{A}_\ell$ outperforms $\mathcal{A}_{\min}$ for $\alpha < 0.38$.

  

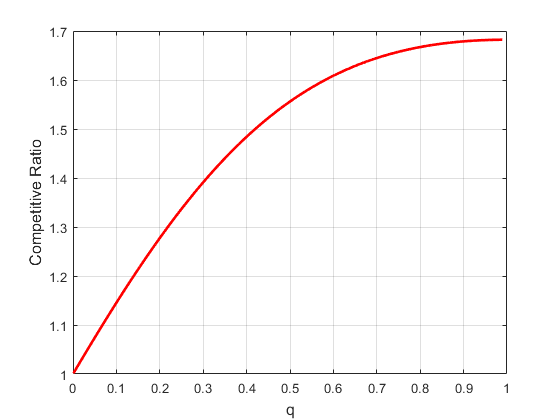
Figure 3: Competitive ratio as a function of parameter $q$: (Left) geometric distribution $G(p)$; (Right) linearly weighted geometric distribution $LG(p)$.

These results suggest that algorithm selection can be adapted to the empirical distribution of output lengths, switching between $\mathcal{A}_{\min}$ and $\mathcal{A}_\ell$ to optimize worst-case guarantees.

Numerical Experiments

The authors conduct extensive experiments on the LMSYS-Chat-1M dataset, simulating LLM inference scheduling under three prediction regimes: rough prediction (wide intervals), non-overlapping classification (bucketed intervals), and individualized overlapping intervals (centered on true $o_i$). Across all settings, $\mathcal{A}_{\min}$ consistently matches or closely approaches the performance of the hindsight-optimal scheduler, even when prediction intervals are extremely wide. In contrast, $\mathcal{A}_{\max}$ only performs well when predictions are highly accurate.

Key empirical findings include:

• Under rough prediction ($[1,1000]$), $\mathcal{A}_{\min}$ achieves average latency nearly identical to H-SF, while $\mathcal{A}_{\max}$ suffers from high latency due to underutilized memory.
• As prediction accuracy improves (narrower intervals), both algorithms improve, but $\mathcal{A}_{\min}$ remains robust even with poor predictions.
• For individualized intervals, $\mathcal{A}_{\min}$ maintains low latency across all levels of prediction uncertainty, while $\mathcal{A}_{\max}$ degrades rapidly as uncertainty increases.

Theoretical and Practical Implications

The results demonstrate that robust, adaptive scheduling algorithms can achieve near-optimal LLM inference efficiency even under substantial prediction uncertainty. The key insight is that leveraging only the lower bound of output length predictions, and dynamically updating estimates during execution, is sufficient to guarantee strong performance both in theory and in practice. The avoidance of upper bound reliance is particularly advantageous, as upper bounds are typically harder to predict accurately in real-world systems.

The theoretical framework—combining competitive analysis, memory-preserving combinatorial techniques, and Rayleigh quotient spectral analysis—provides a foundation for future work on robust online scheduling under uncertainty. The distributional analysis and adaptive algorithm selection further suggest that practical LLM serving systems can benefit from workload-aware policy switching.

Conclusion

This work advances the theory and practice of LLM inference scheduling by introducing and analyzing robust algorithms that operate effectively under prediction uncertainty. The adaptive lower-bound-based approach of $\mathcal{A}_{\min}$ achieves provably logarithmic competitive ratios and demonstrates strong empirical performance across a range of realistic scenarios. The results have direct implications for the design of scalable, efficient, and robust LLM serving systems, and open avenues for further research on learning-augmented online algorithms and resource-constrained scheduling in AI systems.