Intuition emerges in Maximum Caliber models at criticality (2508.06477v1)

Abstract: Whether large predictive models merely parrot their training data or produce genuine insight lacks a physical explanation. This work reports a primitive form of intuition that emerges as a metastable phase of learning that critically balances next-token prediction against future path-entropy. The intuition mechanism is discovered via mind-tuning, the minimal principle that imposes Maximum Caliber in predictive models with a control temperature-like parameter $\lambda$. Training on random walks in deterministic mazes reveals a rich phase diagram: imitation (low $\lambda$), rule-breaking hallucination (high $\lambda$), and a fragile in-between window exhibiting strong protocol-dependence (hysteresis) and multistability, where models spontaneously discover novel goal-directed strategies. These results are captured by an effective low-dimensional theory and frame intuition as an emergent property at the critical balance between memorizing what is and wondering what could be.

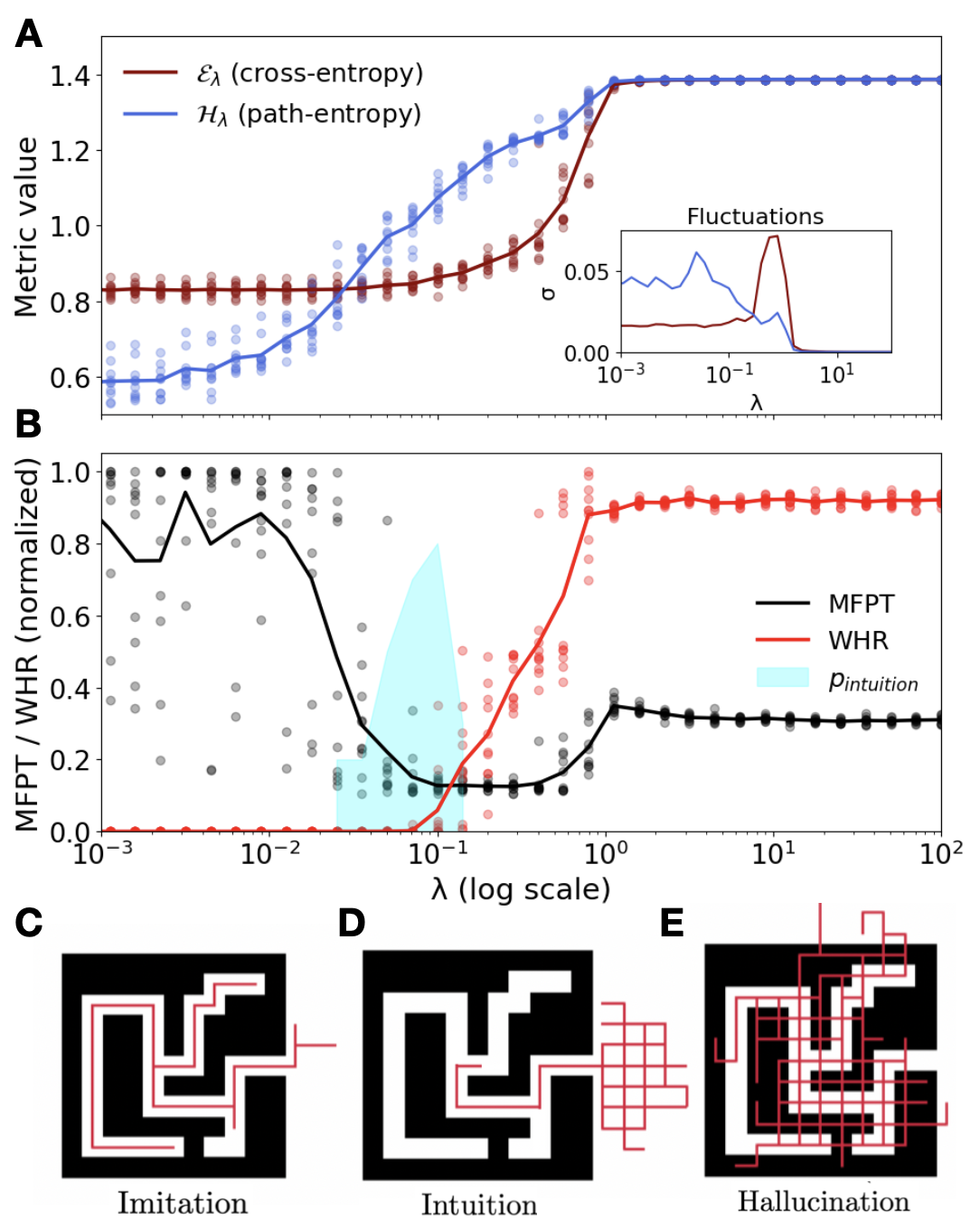
• The paper demonstrates that intuition emerges at a critical λ value, allowing models to shift from mere imitation to finding optimal solutions in maze navigation.
• It employs a phase diagram that distinguishes between imitation at low λ, hallucination at high λ, and a stable intuition phase in between.
• The research bridges experimental results with theoretical predictions, emphasizing the role of path entropy and sufficient exploration in emergent reasoning.

Intuition Emerges in Maximum Caliber Models at Criticality

Introduction

The paper "Intuition emerges in Maximum Caliber models at criticality" explores a novel mechanism for emergent intuition in large predictive models by applying the Maximum Caliber (MaxCal) principle. This principle facilitates the discovery of intuition as a metastable phase within models trained on random walks in deterministic mazes. The research investigates the dynamic between predictive imitation and the maximization of future path entropy through a temperature-like parameter, $\lambda$. This balance reveals distinct phases: imitation at low $\lambda$, hallucination at high $\lambda$, and a critical intuition phase in between.

Figure 1: Gedankenexperiment on emergent reasoning. A minimal environment abstracts a reasoning task into its essential components: a constrained space (a maze) and a hidden, optimal solution (to escape).

Experimental Framework

The research presents a sophisticated framework for analyzing emergent reasoning through a controlled experiment. The environment is modeled as a maze tasked with learning the optimal escape route without prior intelligent data or external rewards. The MaxCal principle is applied with mind-tuning, where $\lambda$ controls the trade-off between log-likelihood of observed data and causal path entropy.

Generating trajectories via the policy $\pi_{\theta,\beta}$ hinges on maximizing entropy in path diversity. The potential solutions are distilled into a free-energy functional $\mathcal{F}_{\lambda,\beta,\tau}(\theta)$ that evaluates this balance. This functional consists of cost terms that measure Cross-Entropy and causal path-entropy, contributing to the system's ability to develop novel strategies beyond simple imitation.

Emergent Phases and Phase Transitions

The investigation reveals a complex phase diagram with three distinct behavioral regimes:

• Imitation: At low $\lambda$, the model demonstrates poor generalization, replicating the random walk training data with high mean first-passage time (MFPT) to the exit.
• Hallucination: At high $\lambda$, while path diversity increases, adherence to the maze constraints diminishes, leading to rule-breaking strategies.
• Intuition Phase: Between these extremes lies a critical region where $\lambda$ facilitates the emergence of optimal, non-trivial solutions with minimal MFPT and zero wall-hit ratio.

  Figure 2: Experimental phase diagram. Sweeping $\lambda$ reveals three behavioral phases.

The phase transitions demonstrate hysteresis and protocol-dependence. As shown, forward sweeps of $\lambda$ can transition the system into the intuition state, though reverse sweeps might not retrace this path, indicating multistability.

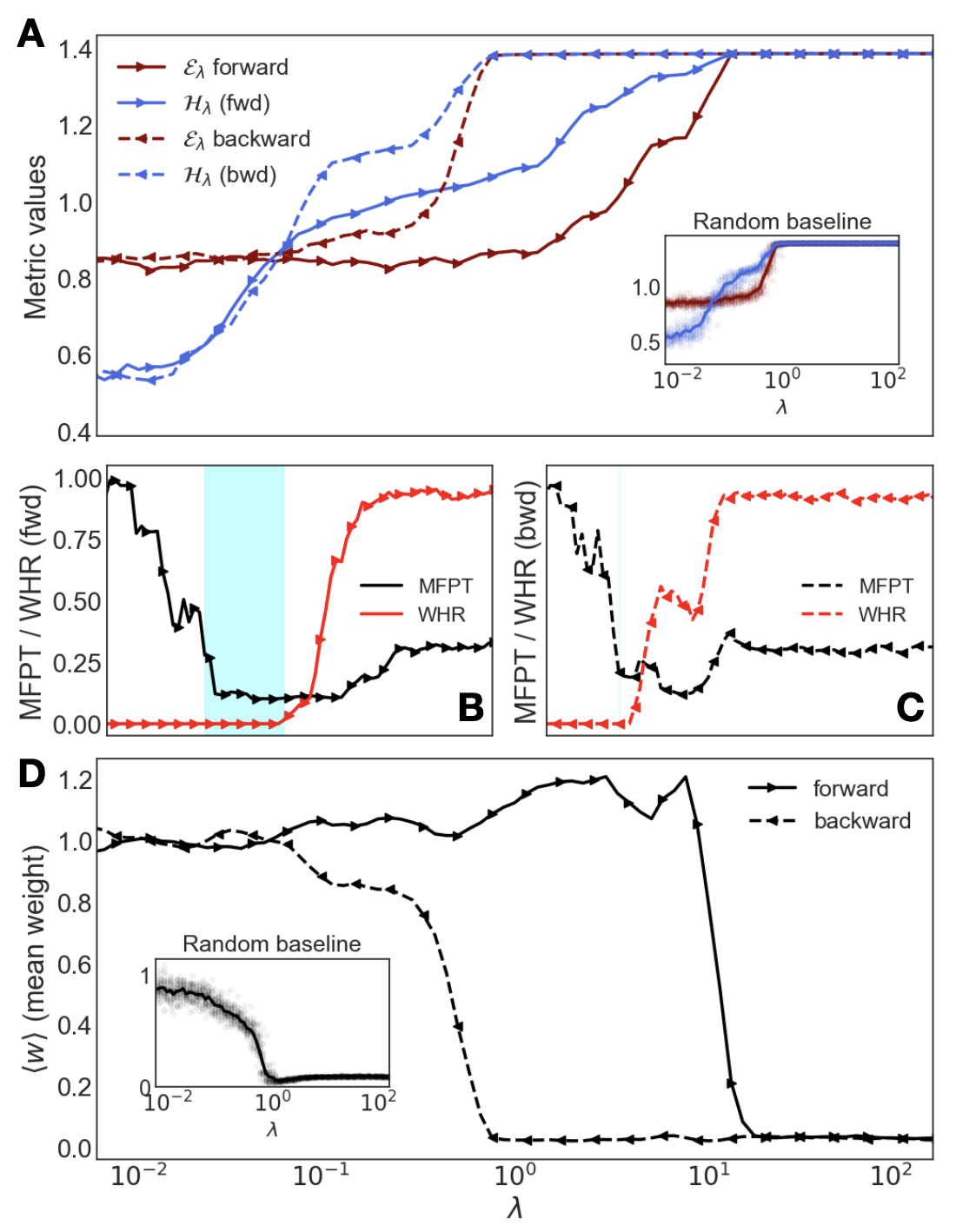
Figure 3: Hysteresis and protocol-dependence. Comparing a forward (solid) and backward (dashed) sweep of $\lambda$ reveals that the intuitive state is stable once found.

Theoretical and Practical Implications

Theoretical insights from a low-dimensional model support experimental findings, emphasizing the dependence on parameters such as future horizon $\tau$ and network capacity. For the intuition phase to manifest, models require sufficient exploration time and representational capacity. The implications extend to conceptualizing intelligence as a phase transition criticality phenomenon, drawing parallels to systems poised at the "edge of chaos," where adaptability and creativity peak.

Figure 4: Theoretical predictions. The low-dimensional model reproduces the experimental findings.

Future Developments and Challenges

Despite empirical demonstration in a controlled environment, applying mind-tuning principles in complex real-world scenarios presents challenges. The combinatorial explosion of calculating path-entropy for long horizons necessitates innovative sampling strategies, such as those inspired by human cognitive processes like dreaming. The alignment of entropic pressures with safety and interpretability remains a core issue in pursuing AGI. Yet, the framework hints at a paradigm scanning for broader applications in reasoning and planning by representing intelligence as a physical phenomenon emerging at criticality.

Conclusion

This research advances the discourse on artificial intuition in predictive models, providing a robust framework grounded in Maximum Caliber theory. By mapping a phase diagram of intuition, the paper enriches the understanding of cognitive phase transitions in AI. While these findings are established in minimal settings, they invite future exploration into the vast, potentially uncharted space of emergent cognition across various AI applications.