On the Expressiveness of Softmax Attention: A Recurrent Neural Network Perspective (2507.23632v1)

Abstract: Since its introduction, softmax attention has become the backbone of modern transformer architectures due to its expressiveness and scalability across a wide range of tasks. However, the main drawback of softmax attention is the quadratic memory requirement and computational complexity with respect to the sequence length. By replacing the softmax nonlinearity, linear attention and similar methods have been introduced to avoid the quadratic bottleneck of softmax attention. Despite these linear forms of attention being derived from the original softmax formulation, they typically lag in terms of downstream accuracy. While strong intuition of the softmax nonlinearity on the query and key inner product suggests that it has desirable properties compared to other nonlinearities, the question of why this discrepancy exists still remains unanswered. This work demonstrates that linear attention is an approximation of softmax attention by deriving the recurrent form of softmax attention. Using this form, each part of softmax attention can be described in the language of recurrent neural networks (RNNs). Describing softmax attention as an RNN allows for the ablation of the components of softmax attention to understand the importance of each part and how they interact. In this way, our work helps explain why softmax attention is more expressive than its counterparts.

• The paper introduces a recurrent formulation of softmax attention using a Taylor series, linking it directly to RNNs.
• It demonstrates that linear attention, as a first-order approximation, lacks the higher-order interactions crucial for expressiveness.
• The study shows that simple vector norm normalization achieves stability and performance, guiding efficient attention mechanism designs.

On the Expressiveness of Softmax Attention: A Recurrent Neural Network Perspective

Introduction

The paper "On the Expressiveness of Softmax Attention: A Recurrent Neural Network Perspective" (2507.23632) provides a rigorous theoretical and empirical analysis of the expressiveness gap between softmax attention and its linearized variants. The authors derive a recurrent formulation of softmax attention using a Taylor series expansion, establishing a direct connection between softmax attention and recurrent neural networks (RNNs). This framework enables a principled comparison of softmax and linear attention, clarifies the limitations of linear approximations, and motivates new perspectives on normalization and gating in attention mechanisms.

Recurrent Formulation of Softmax Attention

The core methodological contribution is the derivation of a recurrent form for softmax attention. By expanding the exponential in the softmax numerator via a Taylor series, the authors show that softmax attention can be interpreted as an infinite sum of RNNs, each corresponding to a different order of interaction between the query and key vectors. Specifically, the $n$-th term in the expansion models $n$-way multiplicative interactions via Kronecker products, with each term weighted by $1/n!$. The hidden state for each RNN grows exponentially with $n$, capturing increasingly complex combinatorial dependencies.

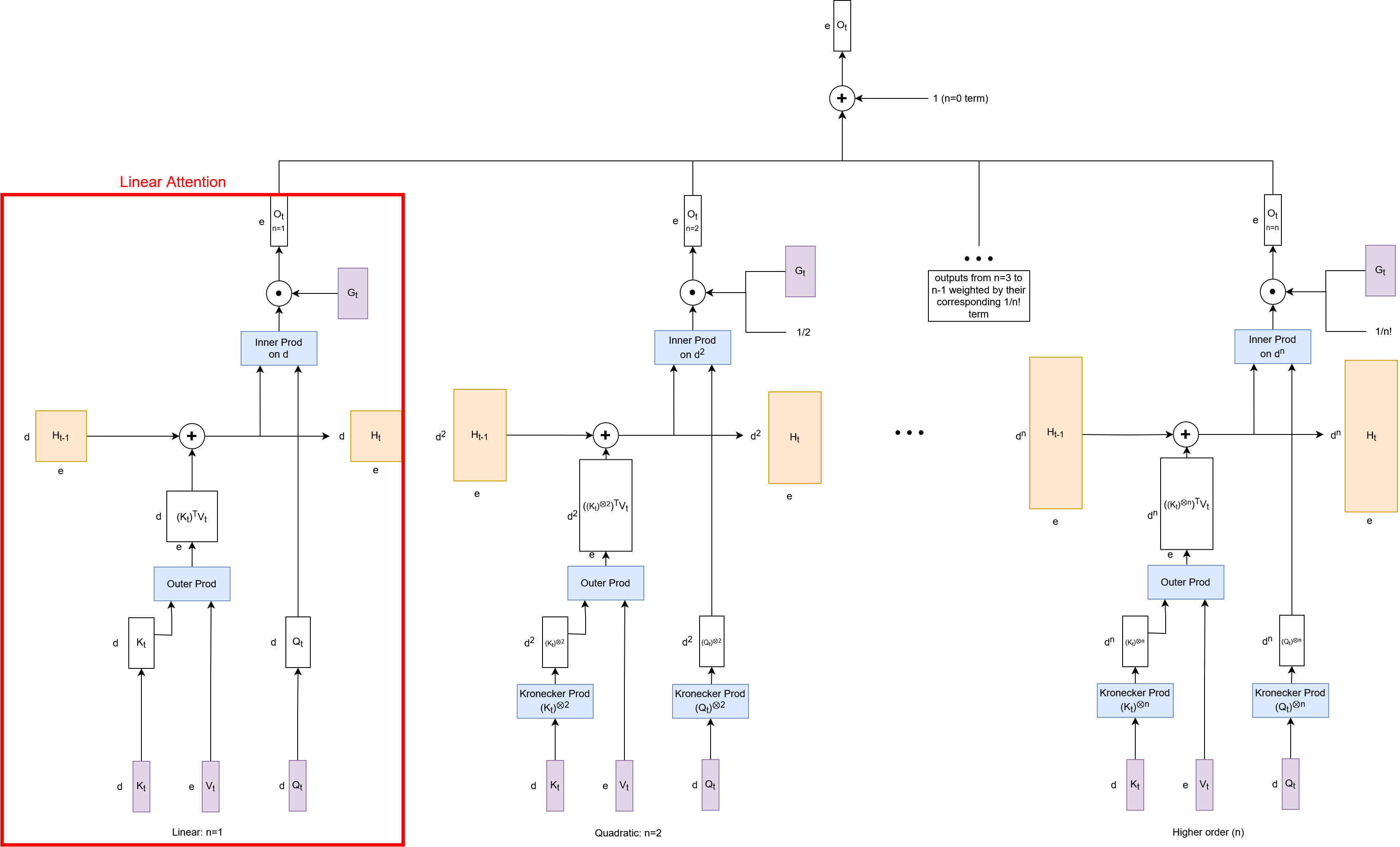
Figure 1: Softmax attention as an RNN. We define $G_t$ in place for the softmax denominator. Linear attention is equivalent to the $n=1$, first order, term.

This formulation reveals that linear attention is simply the first-order ($n=1$) approximation of softmax attention, lacking the higher-order interaction terms that confer additional expressiveness. The recurrent view also enables a reinterpretation of the softmax denominator as a gating or normalization mechanism, analogous to gates in LSTMs or GRUs.

Empirical Evaluation: Equivalence and Scaling

The authors empirically validate their theoretical claims by training Llama 2 models with various attention mechanisms on large-scale LLMing datasets (The Pile, SlimPajama, FineWeb). They compare standard softmax attention, their proposed recurrent/norm-based alternatives, and several linear attention variants. The results demonstrate that replacing the softmax denominator with a vector norm (e.g., $L_2$) yields performance nearly indistinguishable from standard softmax, while gating-based alternatives are less stable.

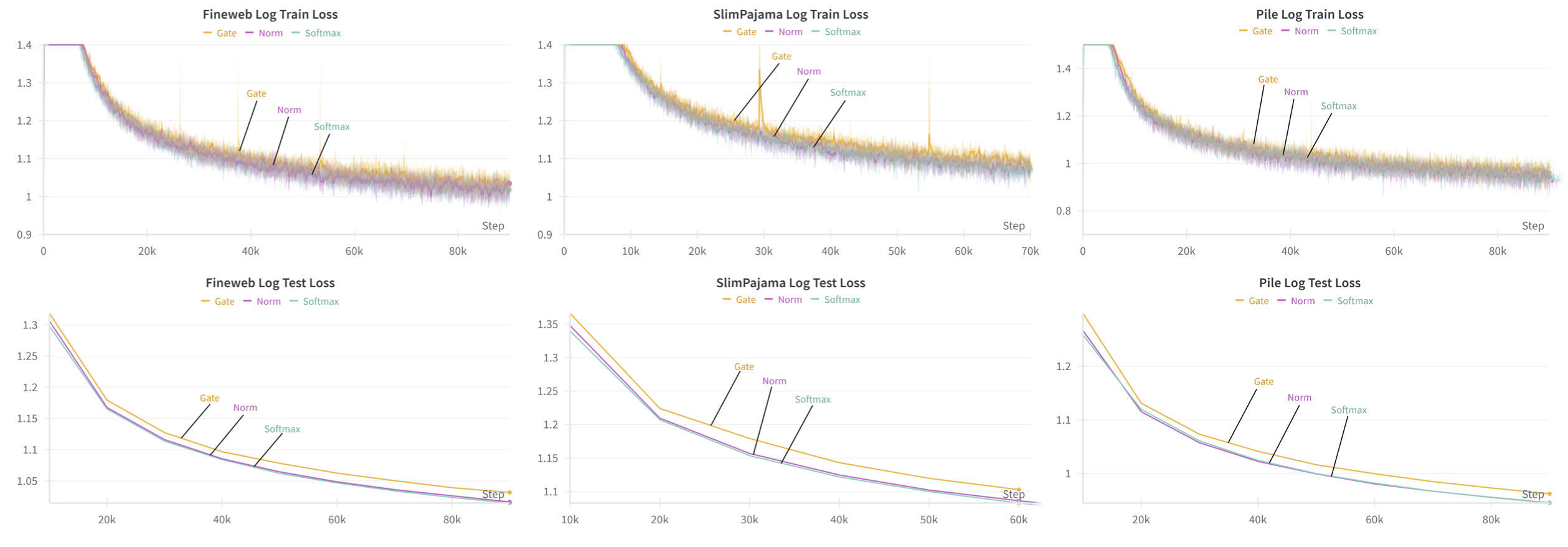
Figure 2: Test and train loss on various datasets for softmax attention and the proposed methods with gate or norm replacements.

Scaling experiments show that the norm-based recurrent formulation matches softmax attention in both model size and sequence length scaling regimes, confirming the robustness of the theoretical insights.

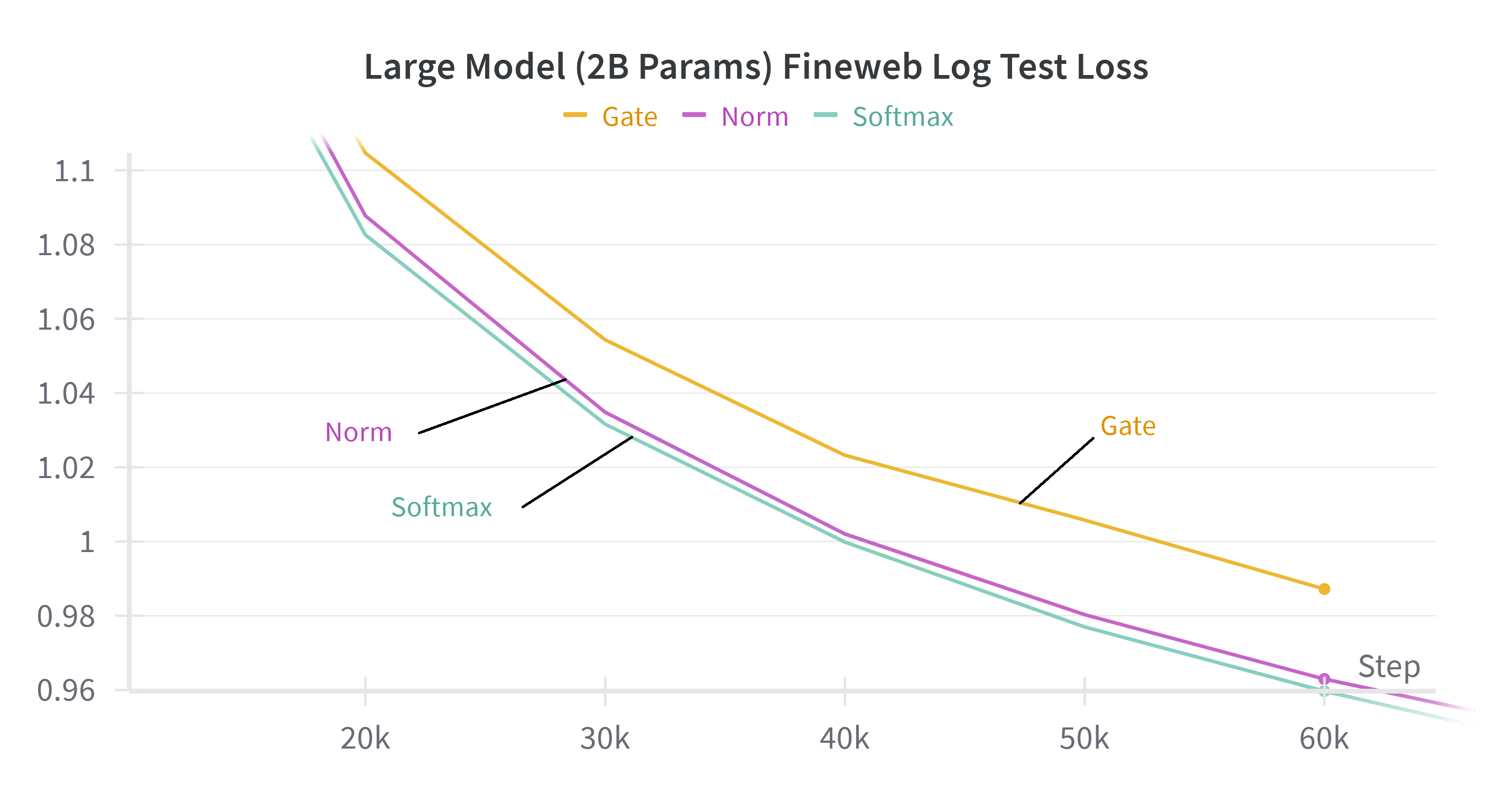
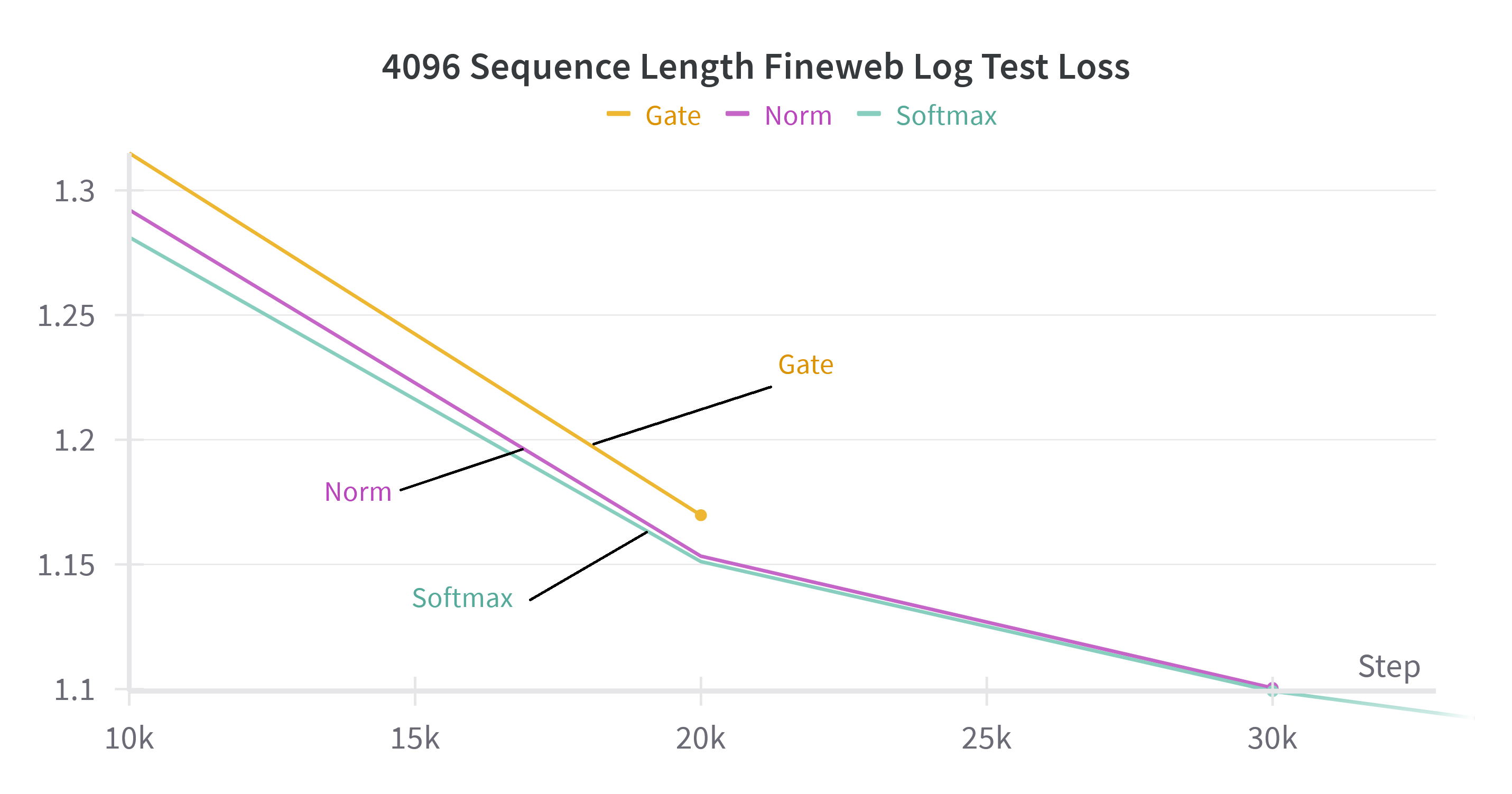
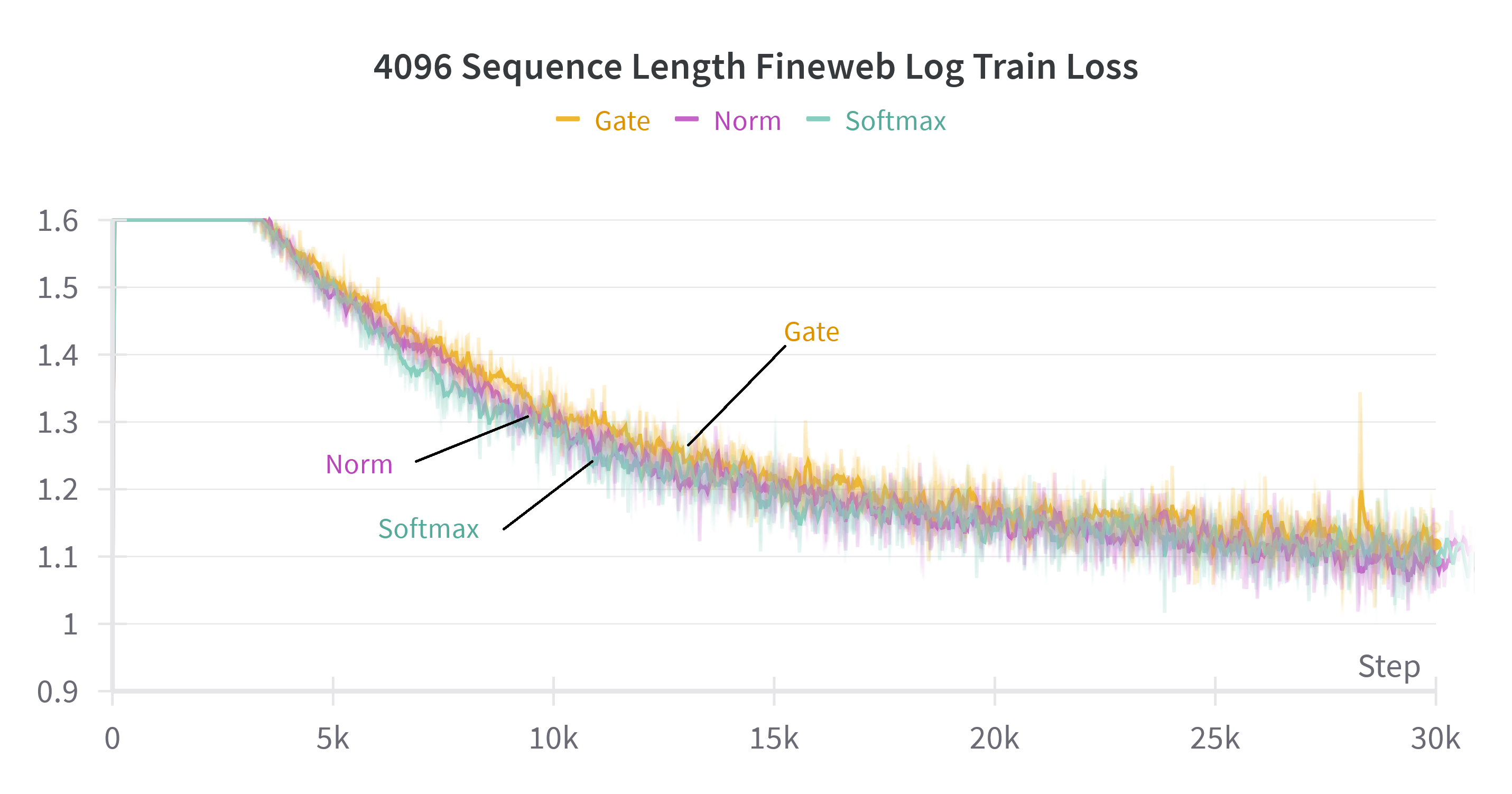
Figure 3: Test and train loss on the FineWeb dataset for large models (about 2B parameters) on 1024 sequence length and small models (about 300 million parameters) on 4096 sequence length for softmax attention and the proposed methods with gate or norm replacements.

Linear Attention as a First-Order Approximation

The recurrent formulation makes explicit that linear attention is a strict subset of softmax attention, capturing only first-order interactions. Empirical results confirm a significant performance gap between linear and softmax attention, even when advanced kernelizations or gating are applied to linear attention.

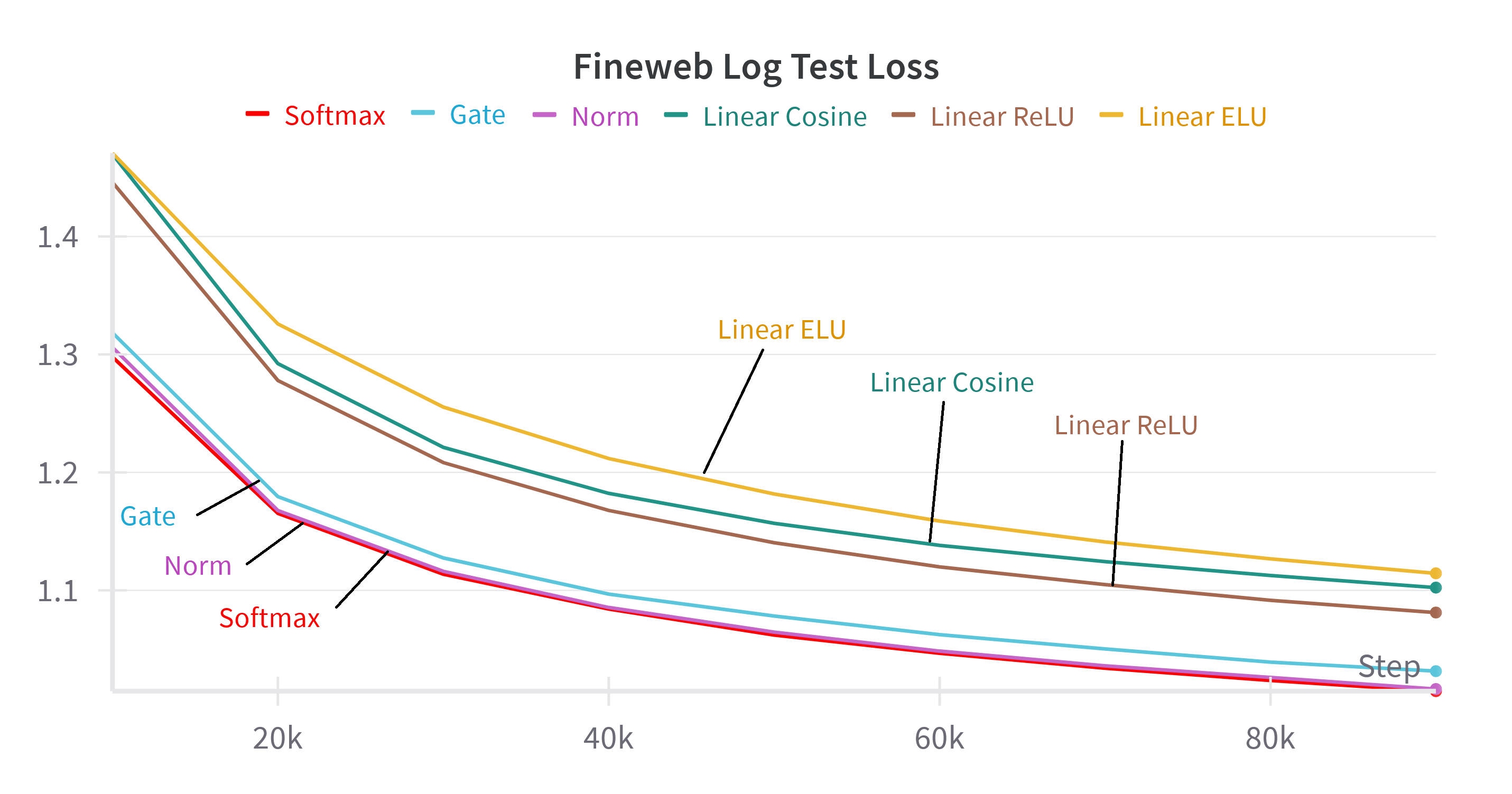
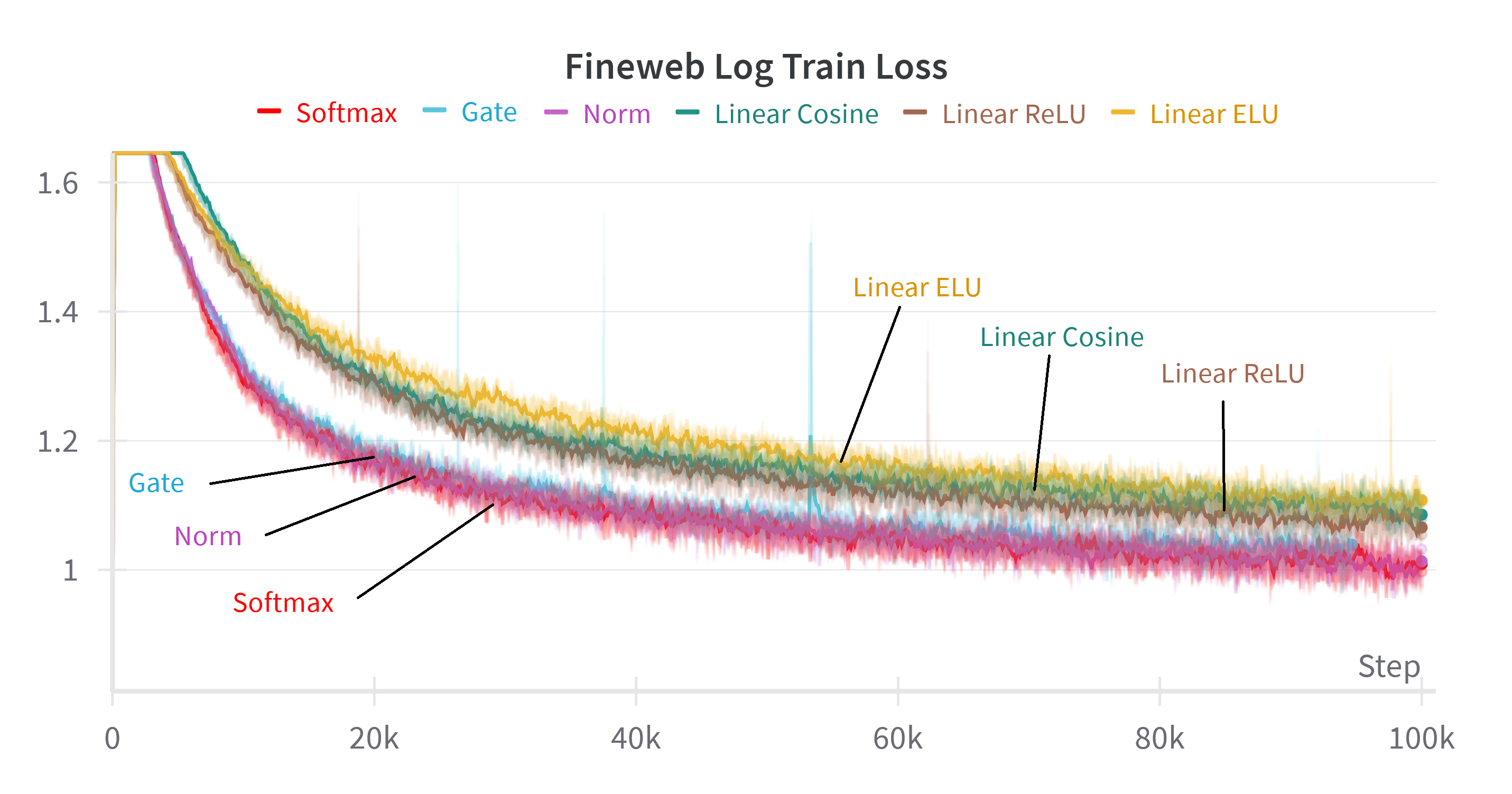
Figure 4: Test and train loss on the FineWeb dataset for various linear attention methods, softmax attention, and the proposed methods with gate or norm replacements.

Taylor Series Expansion and Expressiveness

By incrementally adding higher-order terms from the Taylor expansion to the attention mechanism, the authors show a smooth transition in performance from linear to softmax attention. For softmax, including terms up to $n=10$ suffices to match the full softmax performance. For linear attention variants, adding higher-order terms improves performance but never fully closes the gap, highlighting the fundamental limitation imposed by decomposable kernelizations.

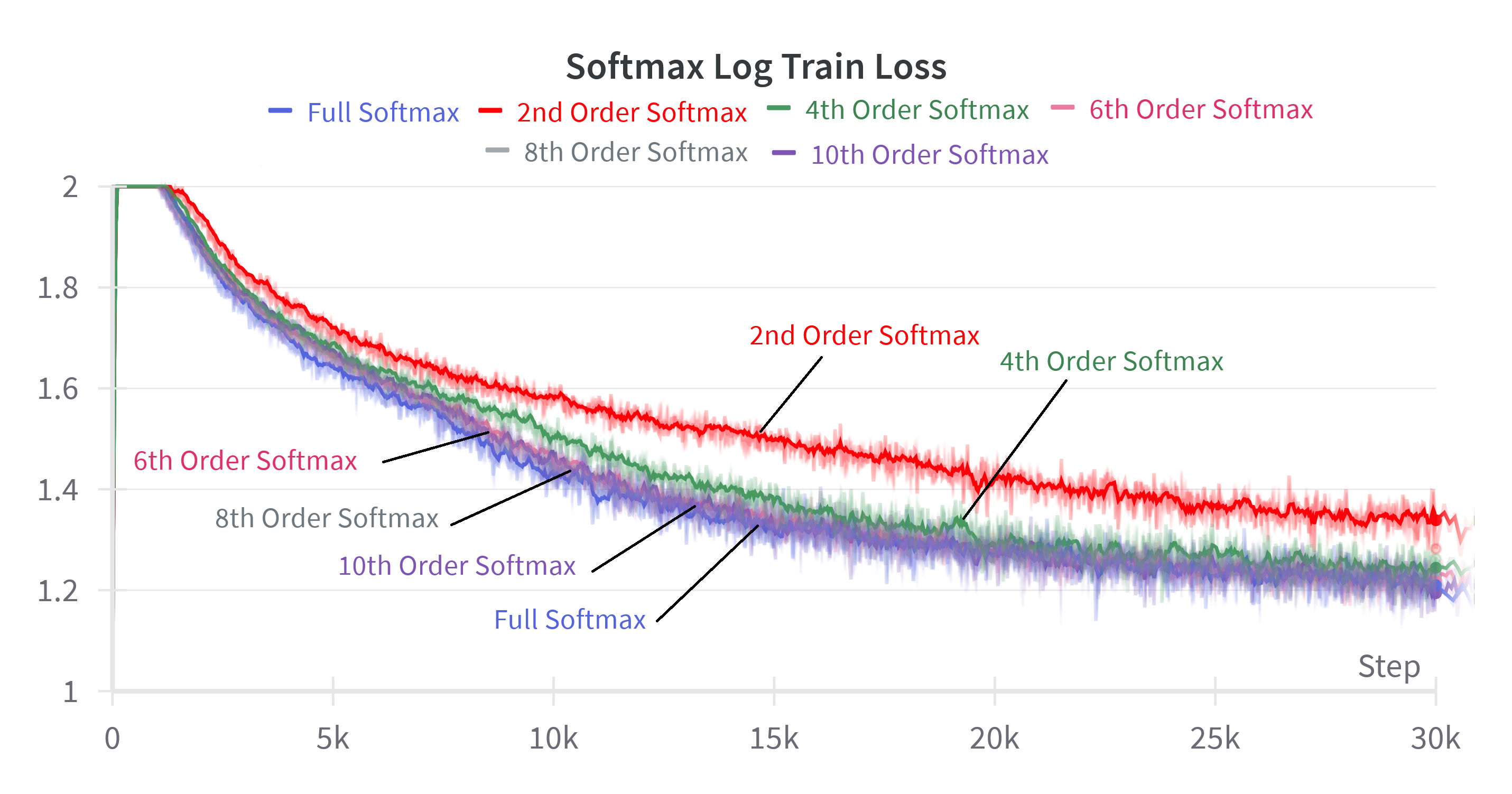
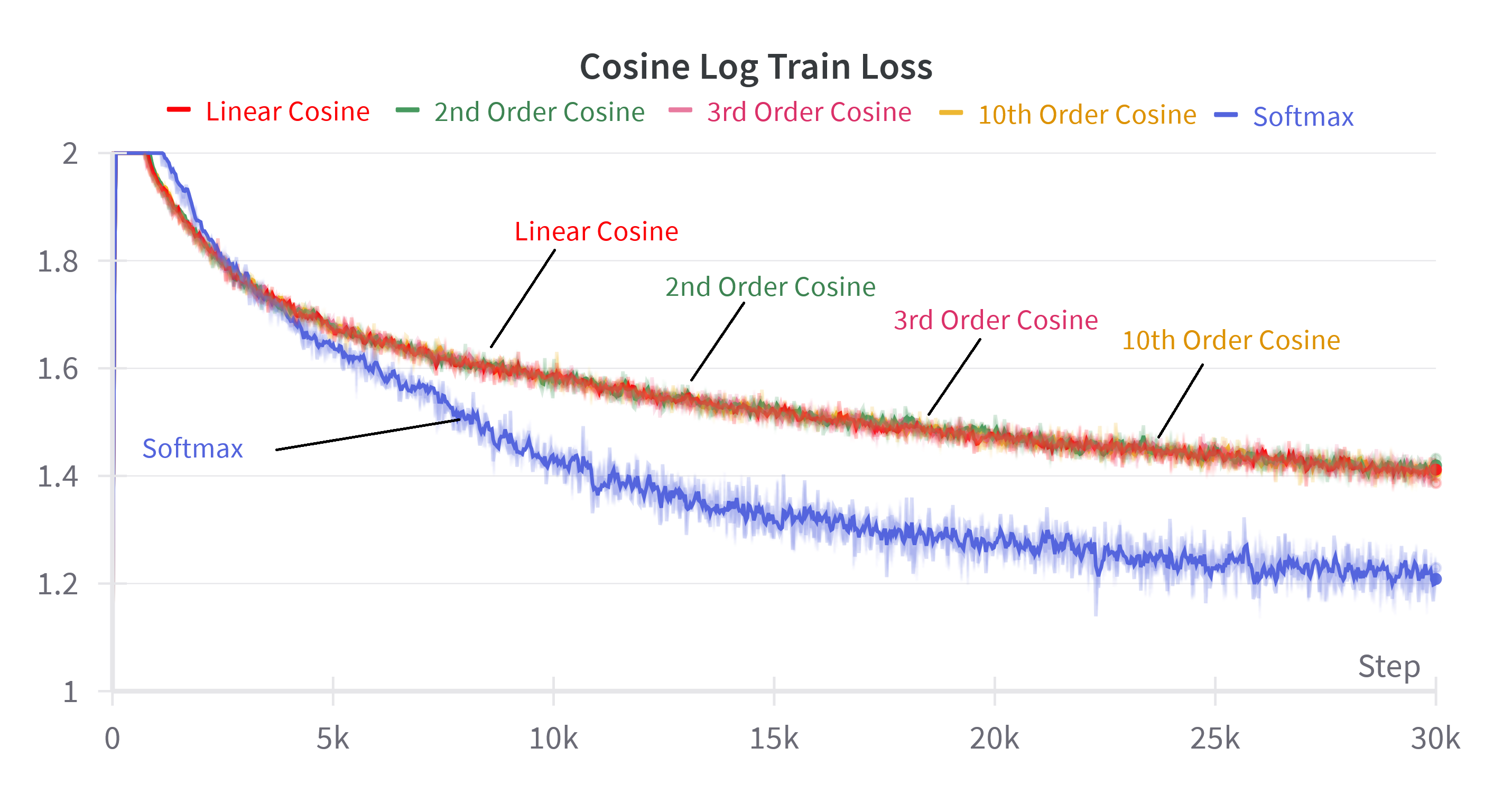
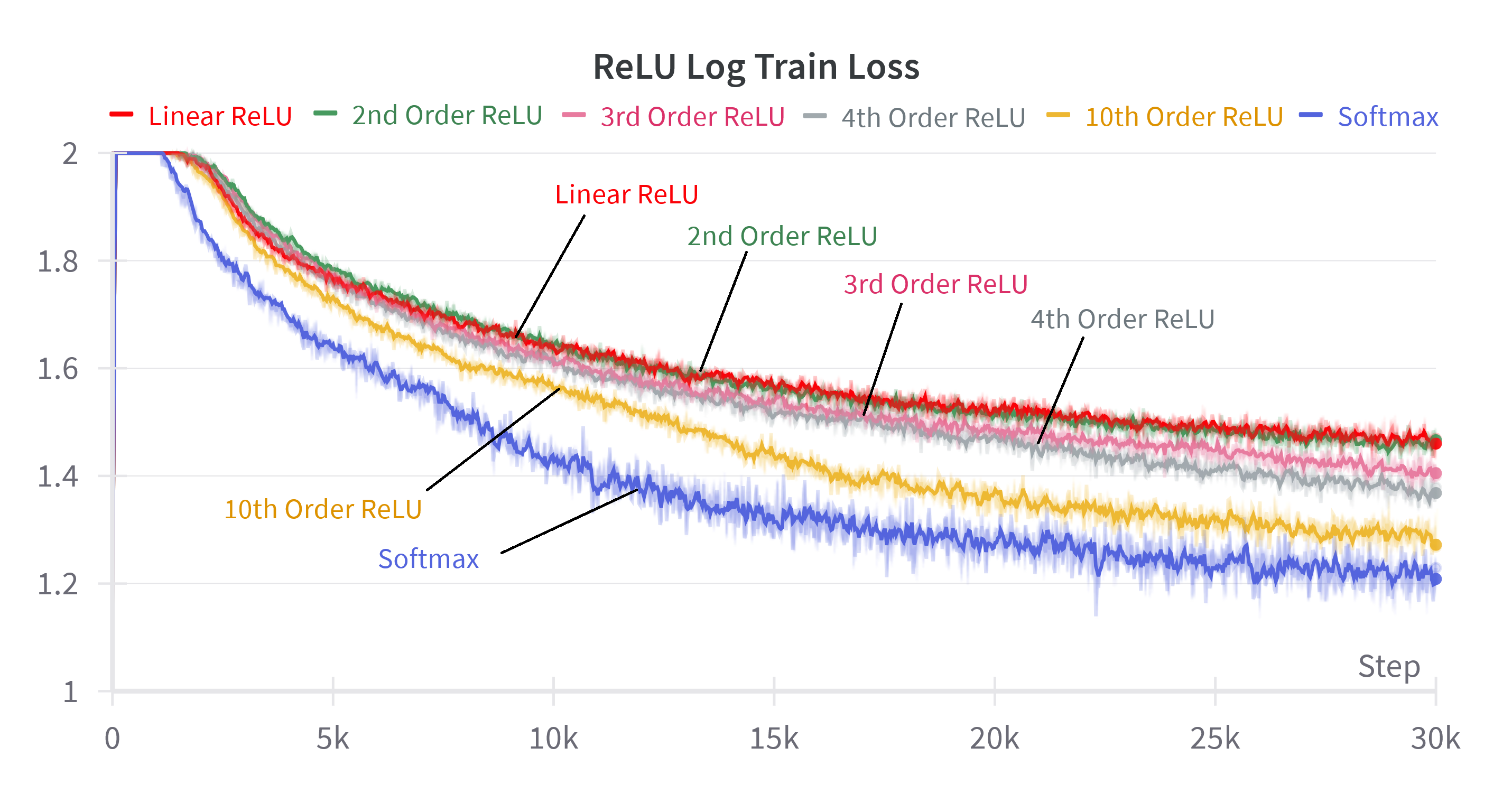
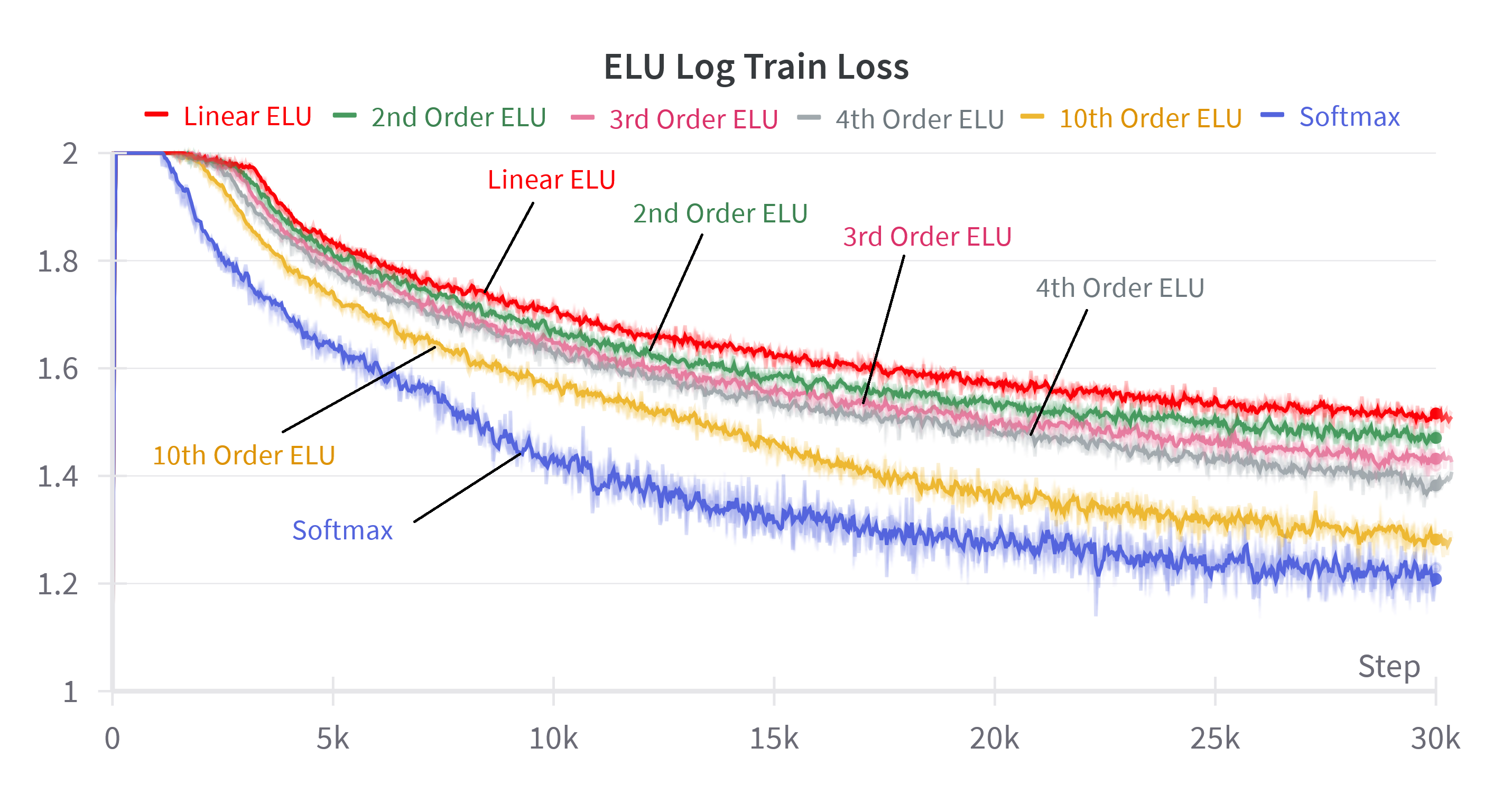
Figure 5: Log train loss for softmax attention and various linear attention method when summing more powers of the inner product. The $n$th order denotes the sum of powers from 0 to $n$.

Ablation Studies: The Role of Normalization and Gating

A comprehensive ablation paper investigates the impact of various normalization and gating strategies on the stability and performance of the recurrent attention formulation. The results indicate that vector norms (e.g., $L_2$, RMS, layer norm) are sufficient to stabilize and match softmax attention, while sequence length normalization and gating alone are less effective. Removing the denominator or detaching it from the computation graph degrades performance and stability.

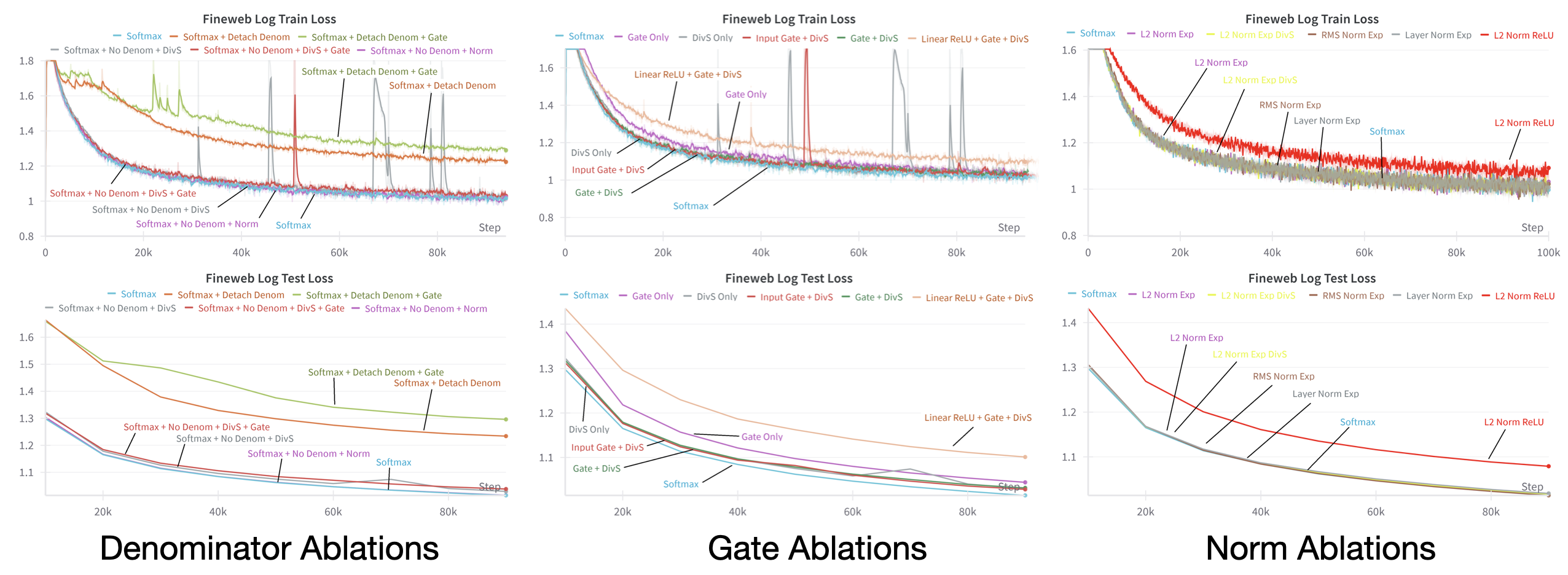
Figure 6: Test and train loss on various datasets for softmax attention and the proposed methods with gate or norm replacements. Expanded plots can be found in Appendix.

Theoretical and Practical Implications

The recurrent perspective unifies softmax and linear attention under a common framework, clarifying the source of softmax attention's superior expressiveness: the ability to model higher-order interactions between queries and keys. The empirical finding that vector norms suffice for normalization suggests that the precise form of the softmax denominator is less critical than previously assumed, provided that some form of normalization is present to stabilize the output.

This insight has several implications:

• Design of Efficient Attention Mechanisms: The recurrent formulation motivates the exploration of higher-order approximations that balance expressiveness and computational tractability, potentially leading to new attention variants that interpolate between linear and softmax attention.
• Hardware and Implementation: Since higher-order terms require exponentially larger hidden states, practical implementations must trade off expressiveness for efficiency. The finding that a 10th-order approximation suffices for softmax-level performance provides a concrete target for hardware-aware design.
• Generalization to Other Architectures: The framework is extensible to more complex recurrent or state-space models (e.g., RWKV, Mamba), suggesting a path toward unifying attention and RNN-based architectures.

Conclusion

This work provides a principled theoretical and empirical analysis of the expressiveness of softmax attention, establishing a direct connection to RNNs via a Taylor series expansion. The results clarify why linear attention is fundamentally less expressive and demonstrate that normalization via vector norms is sufficient for stable and performant attention. These findings inform both the theoretical understanding and practical design of attention mechanisms, with implications for future research on efficient and expressive sequence models. The recurrent perspective may serve as a foundation for further advances in attention architectures, particularly in the context of scaling and hardware efficiency.