Geometry of Neural Reinforcement Learning in Continuous State and Action Spaces (2507.20853v1)

Abstract: Advances in reinforcement learning (RL) have led to its successful application in complex tasks with continuous state and action spaces. Despite these advances in practice, most theoretical work pertains to finite state and action spaces. We propose building a theoretical understanding of continuous state and action spaces by employing a geometric lens to understand the locally attained set of states. The set of all parametrised policies learnt through a semi-gradient based approach induces a set of attainable states in RL. We show that the training dynamics of a two-layer neural policy induce a low dimensional manifold of attainable states embedded in the high-dimensional nominal state space trained using an actor-critic algorithm. We prove that, under certain conditions, the dimensionality of this manifold is of the order of the dimensionality of the action space. This is the first result of its kind, linking the geometry of the state space to the dimensionality of the action space. We empirically corroborate this upper bound for four MuJoCo environments and also demonstrate the results in a toy environment with varying dimensionality. We also show the applicability of this theoretical result by introducing a local manifold learning layer to the policy and value function networks to improve the performance in control environments with very high degrees of freedom by changing one layer of the neural network to learn sparse representations.

• The paper establishes that attainable states concentrate on a low-dimensional manifold bounded by 2dₐ+1.
• It leverages a linearized model of wide neural networks to analyze training dynamics in continuous-time deterministic MDPs.
• The work demonstrates that adding sparsification layers to SAC improves sample efficiency and control performance.

Geometry of Neural Reinforcement Learning in Continuous State and Action Spaces

Introduction and Motivation

This work addresses the theoretical underpinnings of reinforcement learning (RL) in continuous state and action spaces, focusing on the geometric structure of the set of states attainable by neural network (NN) policies. While empirical RL has achieved notable success in high-dimensional continuous domains, most theoretical analyses are limited to finite or discrete settings. The paper leverages the manifold hypothesis, positing that high-dimensional data encountered in RL tasks often reside on low-dimensional manifolds, and provides the first rigorous link between the geometry of the attainable state space and the dimensionality of the action space for neural RL agents.

Theoretical Framework

The analysis is grounded in continuous-time deterministic Markov decision processes (MDPs) with continuous state and action spaces. The agent's policy is parameterized by a two-layer (single hidden layer) neural network with GeLU activation, and the training is performed via semi-gradient policy gradient methods. The key theoretical innovation is the use of a linearized model of wide neural networks, where the width $n \to \infty$, enabling tractable analysis of the training dynamics and their impact on the geometry of the set of attainable states.

The main result establishes that, under mild regularity and smoothness assumptions, the set of states locally attainable by the agent's policy is concentrated around a low-dimensional manifold whose dimension is upper bounded by $2d_a + 1$, where $d_a$ is the action space dimension, independent of the ambient state space dimension $d_s$. This is formalized via a Lie series expansion of the system's dynamics under the neural policy and a careful analysis of the stochastic gradient dynamics in the infinite-width limit.

Empirical Validation

The theoretical claims are substantiated through a series of empirical studies:

• Validation of Linearized Policy Approximation: The returns achieved by canonical (nonlinear) and linearized policies are compared as a function of network width. The difference in returns vanishes as width increases, confirming the adequacy of the linearized model for wide networks.

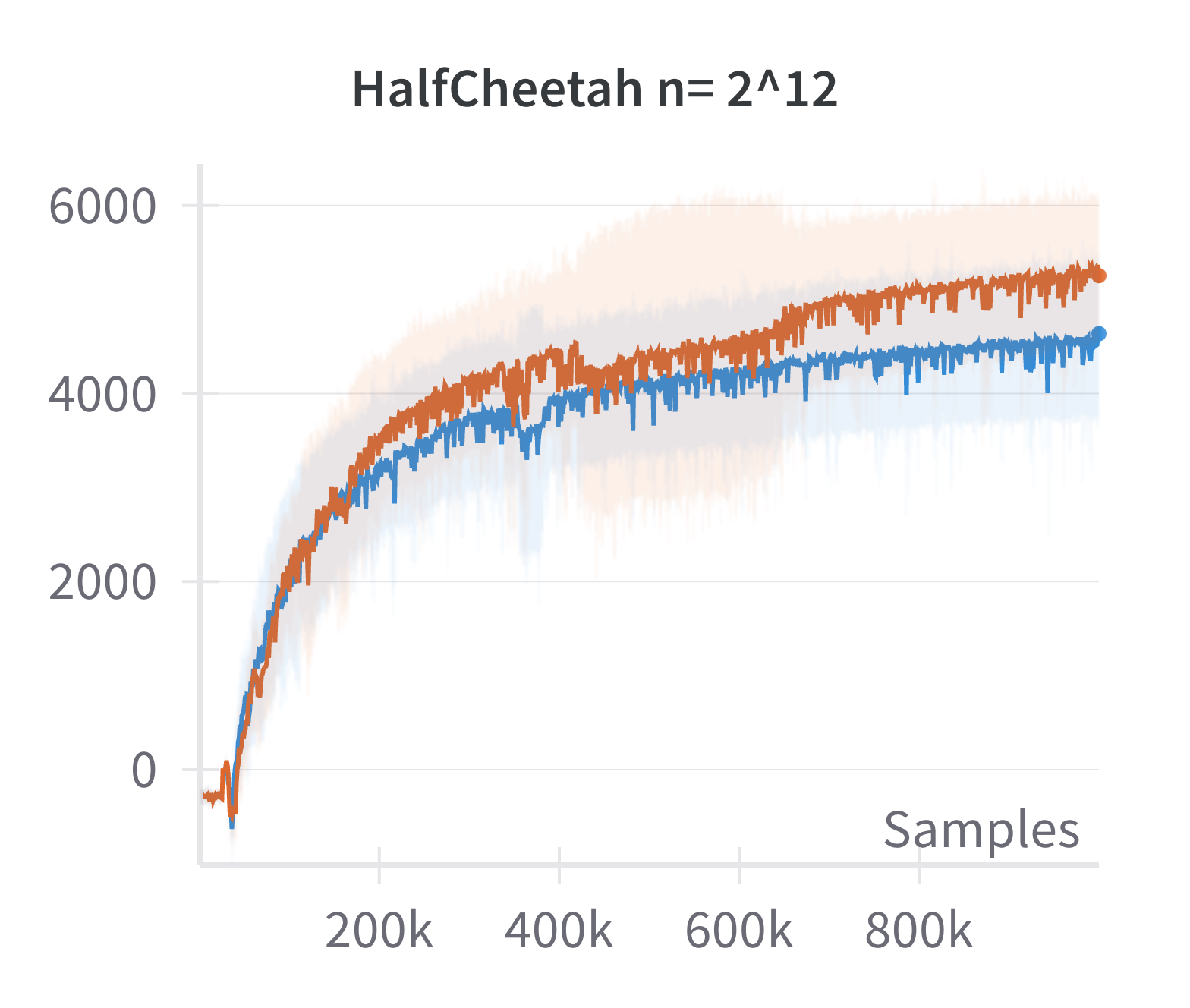
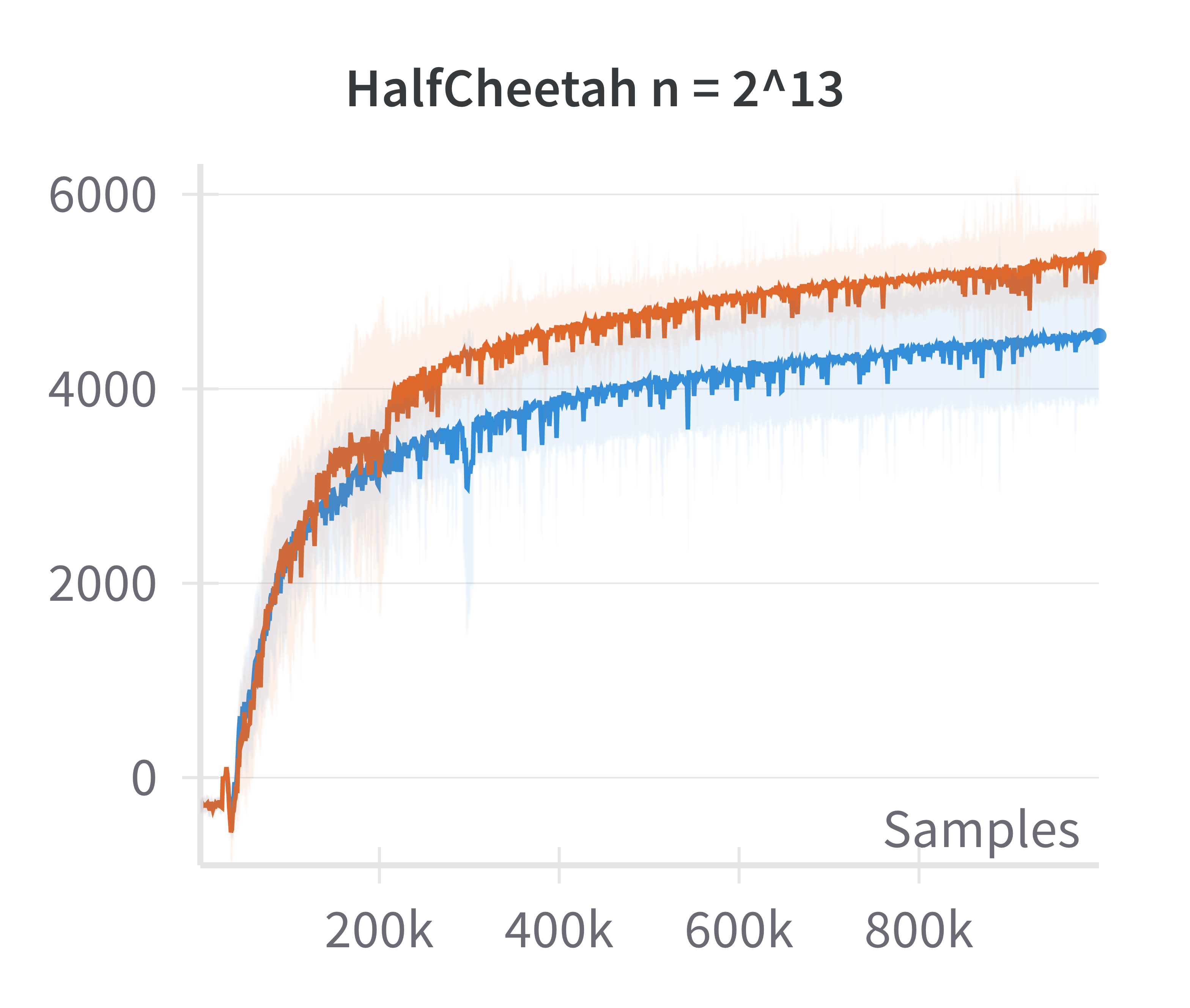
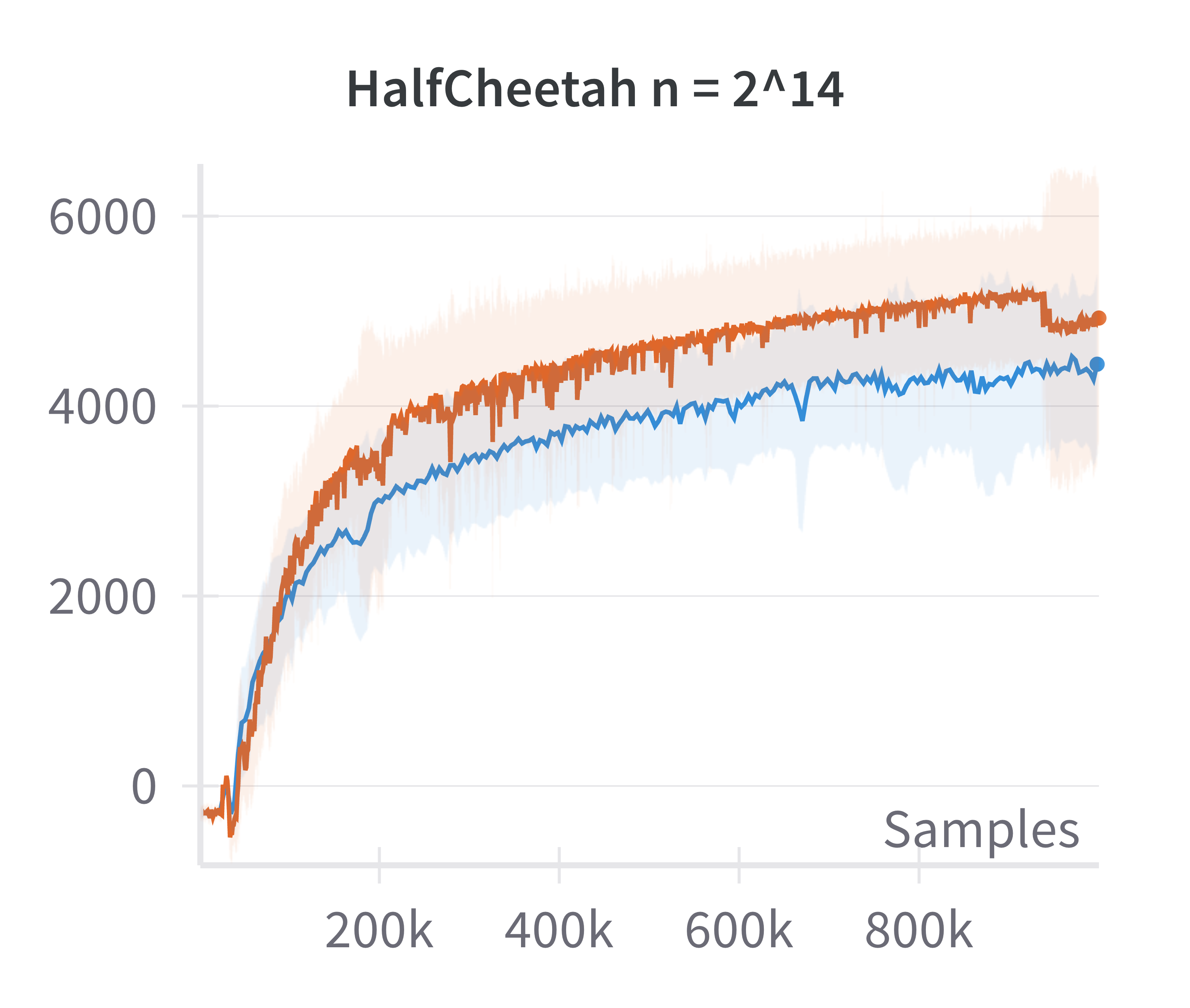
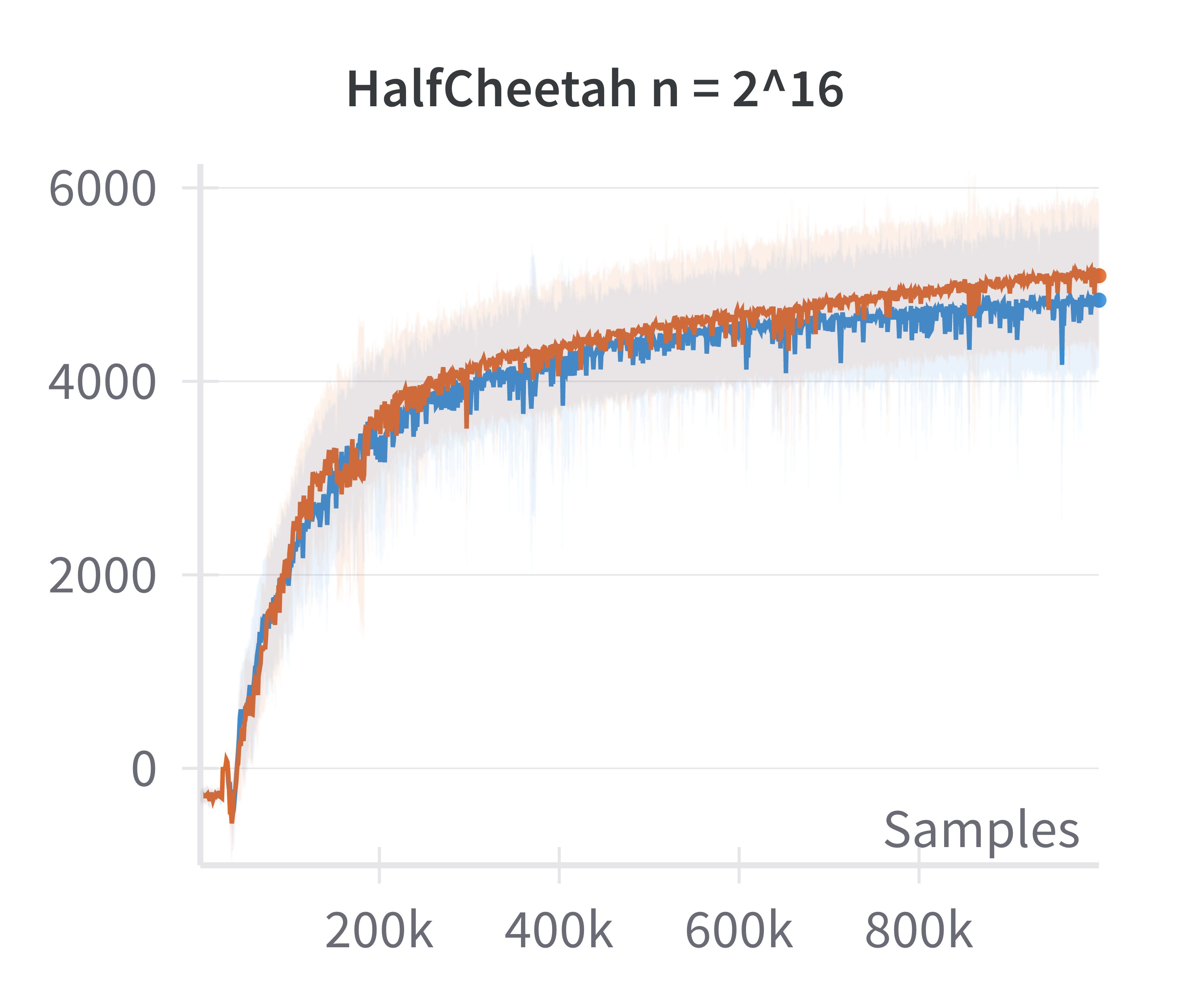
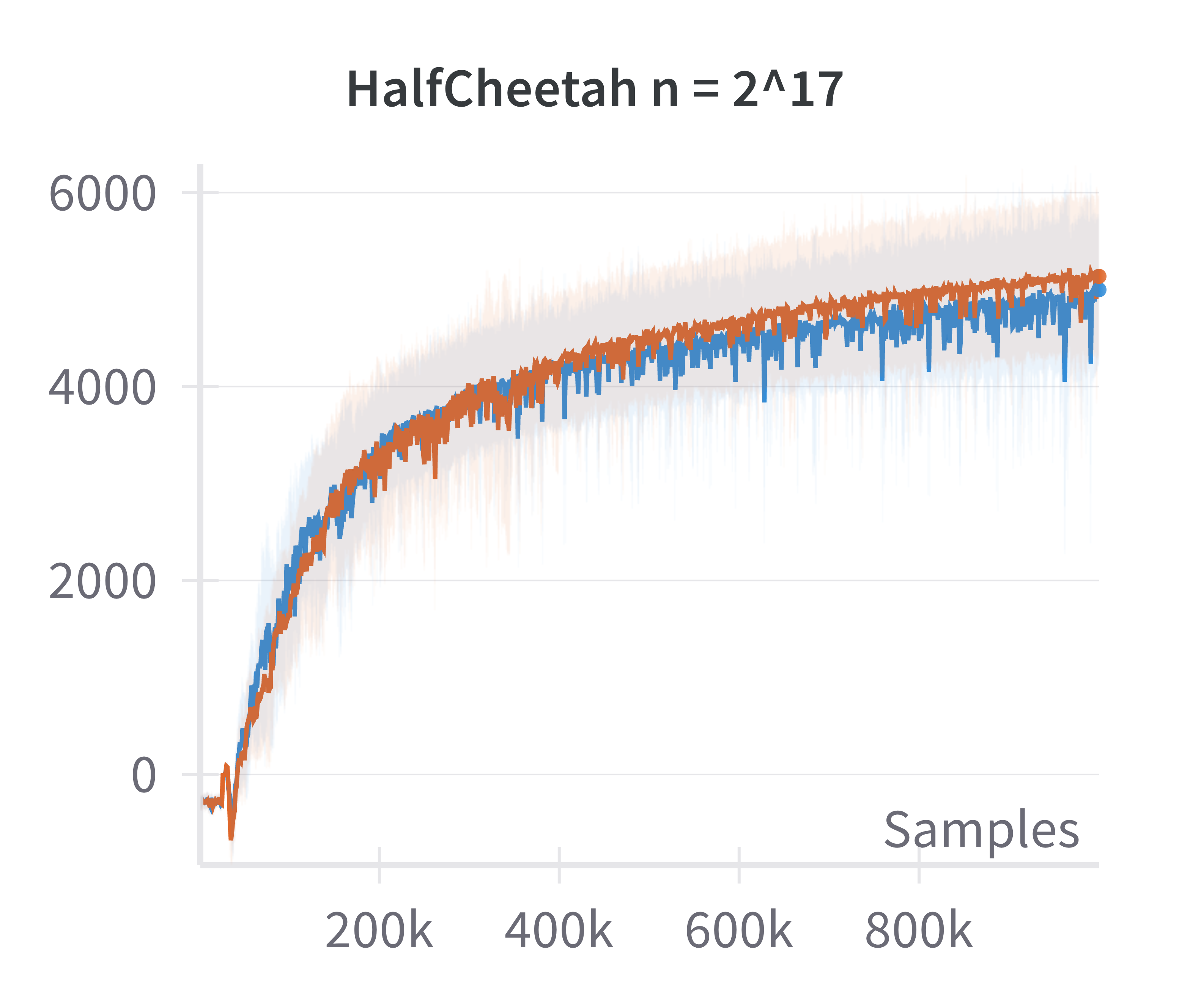
Figure 1: The canonical policy (in red) tracks the returns for linearised policy (in blue) at higher widths ($\log_2 n > 15$).

• Intrinsic Dimensionality Estimation: The intrinsic dimension of the set of attainable states is estimated using the method of Facco et al. across several MuJoCo environments. In all cases, the estimated dimension is significantly below the ambient state dimension and remains below the theoretical upper bound of $2d_a + 1$.

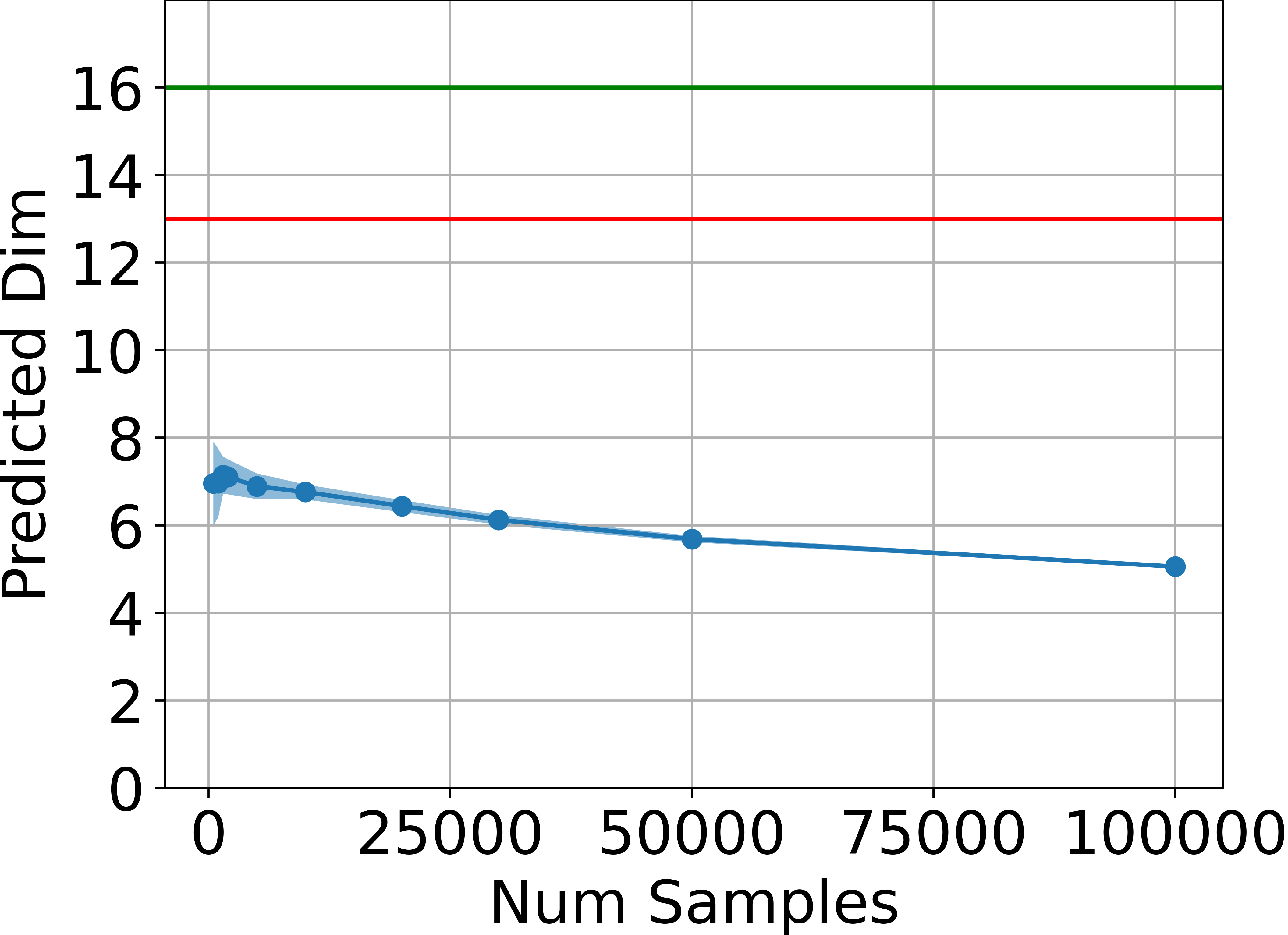
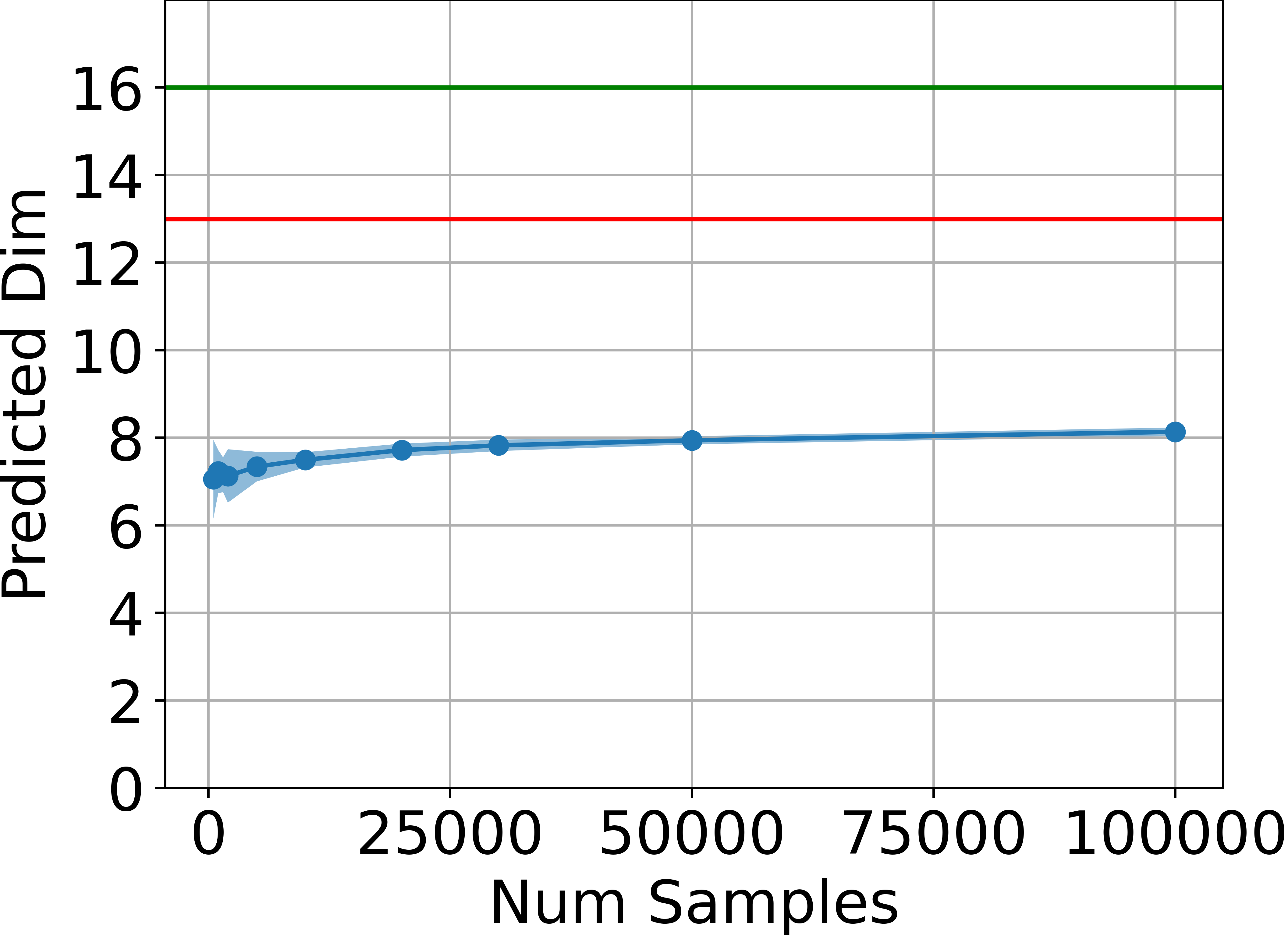
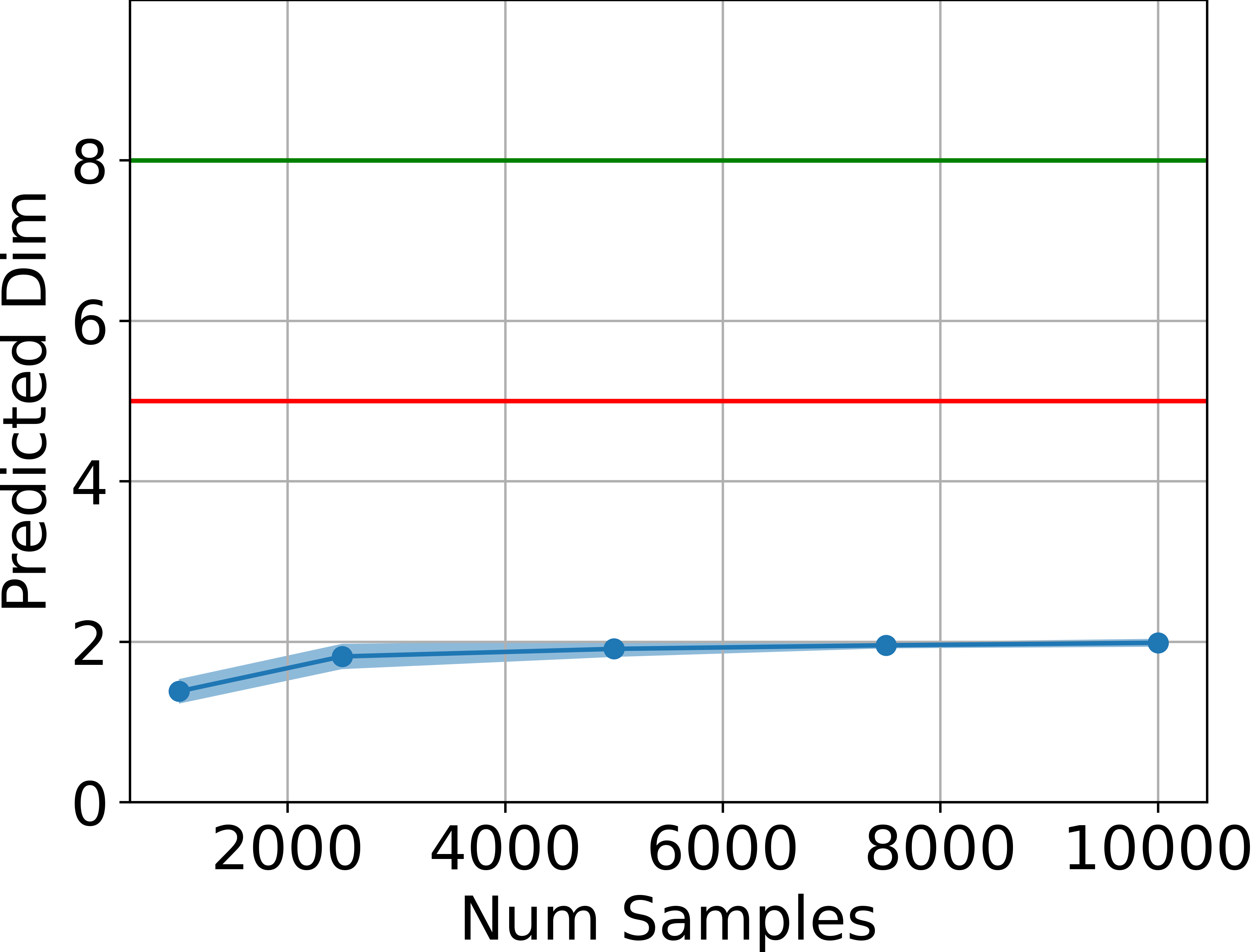
Figure 2: Estimated dimensionality of the attainable states, in blue, is far below $d_s$ (green line) and also below $2 d_a +1$ (red line) for four tasks, estimated using the method by Facco et al.

• Architectural Comparisons: Performance of single hidden layer GeLU networks is shown to be comparable to deeper ReLU networks in standard RL benchmarks, supporting the relevance of the theoretical model.

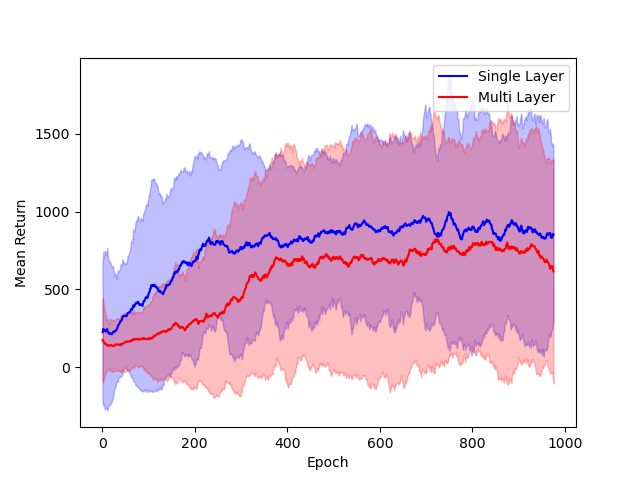
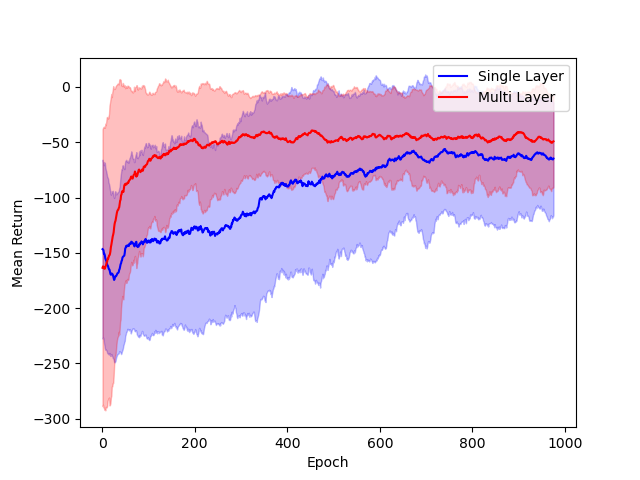
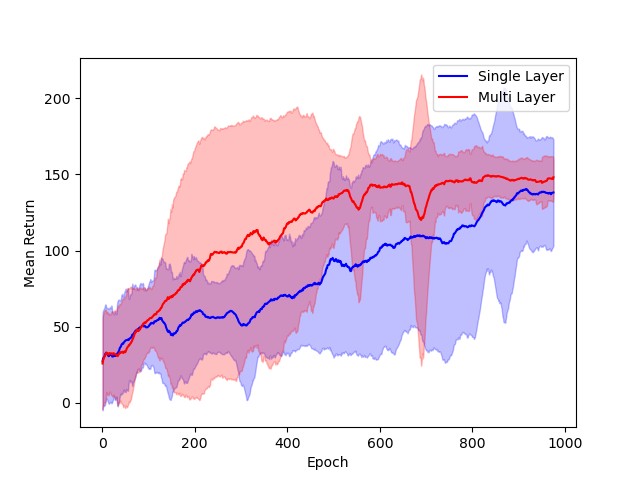
Figure 3: Comparison of single hidden layer with GeLU activation (blue) and multiple hidden layer with ReLU activation (red) architectures for DNNs.

Practical Implications: Sparse Representations and RL Performance

The theoretical insight that attainable states concentrate on a low-dimensional manifold motivates architectural modifications to exploit this structure. Specifically, the paper incorporates a sparsification layer (from the CRATE framework) into the policy and value networks of the Soft Actor-Critic (SAC) algorithm. This layer is designed to learn sparse, low-rank representations aligned with the underlying manifold structure.

Empirical results demonstrate that this modification yields substantial improvements in sample efficiency and final performance, particularly in high-dimensional control tasks (e.g., Ant, Dog Stand, Dog Walk, Quadruped Walk). Notably, the sparse SAC variant outperforms the standard fully connected SAC, especially in environments where the baseline fails to learn effectively.

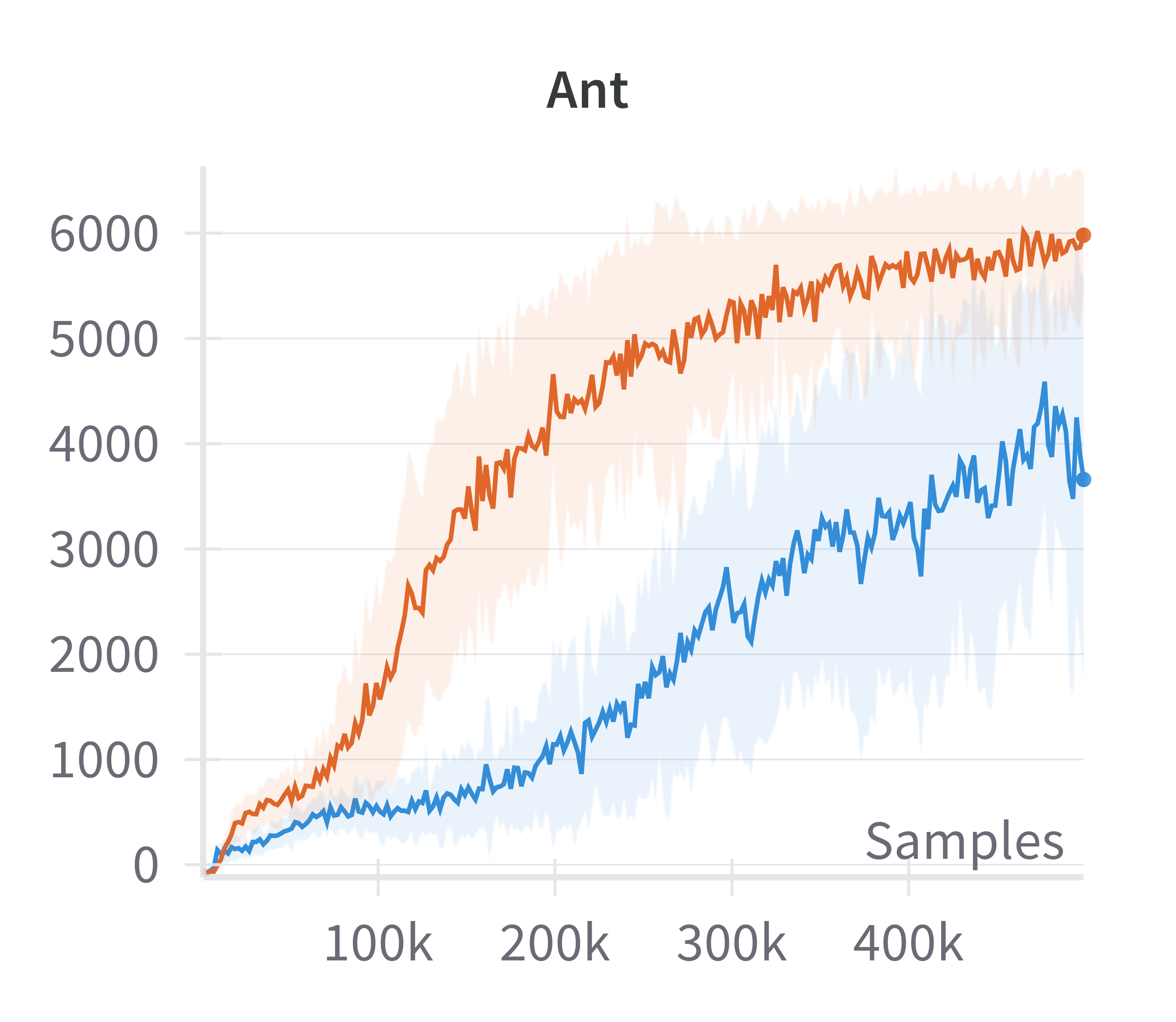
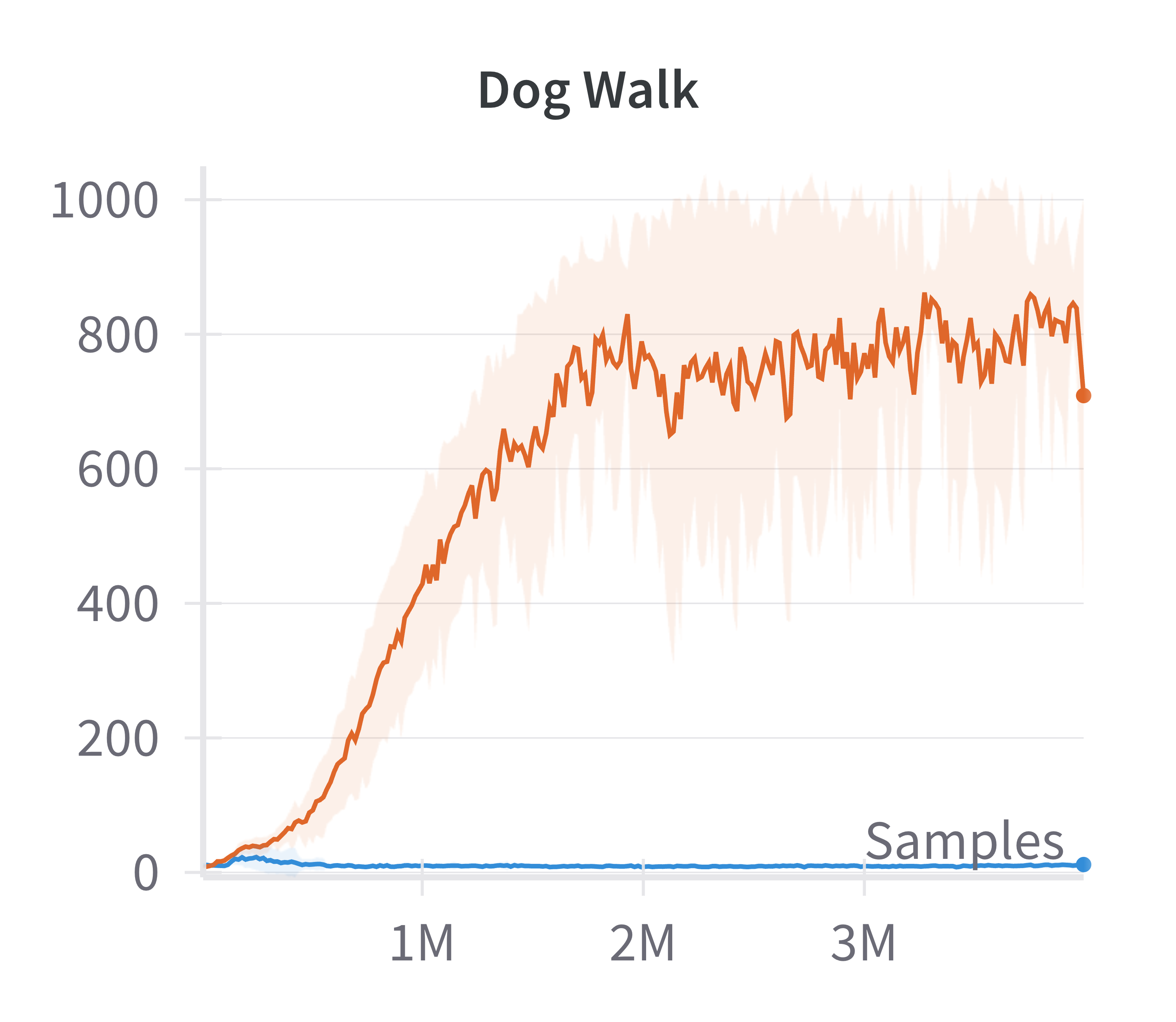
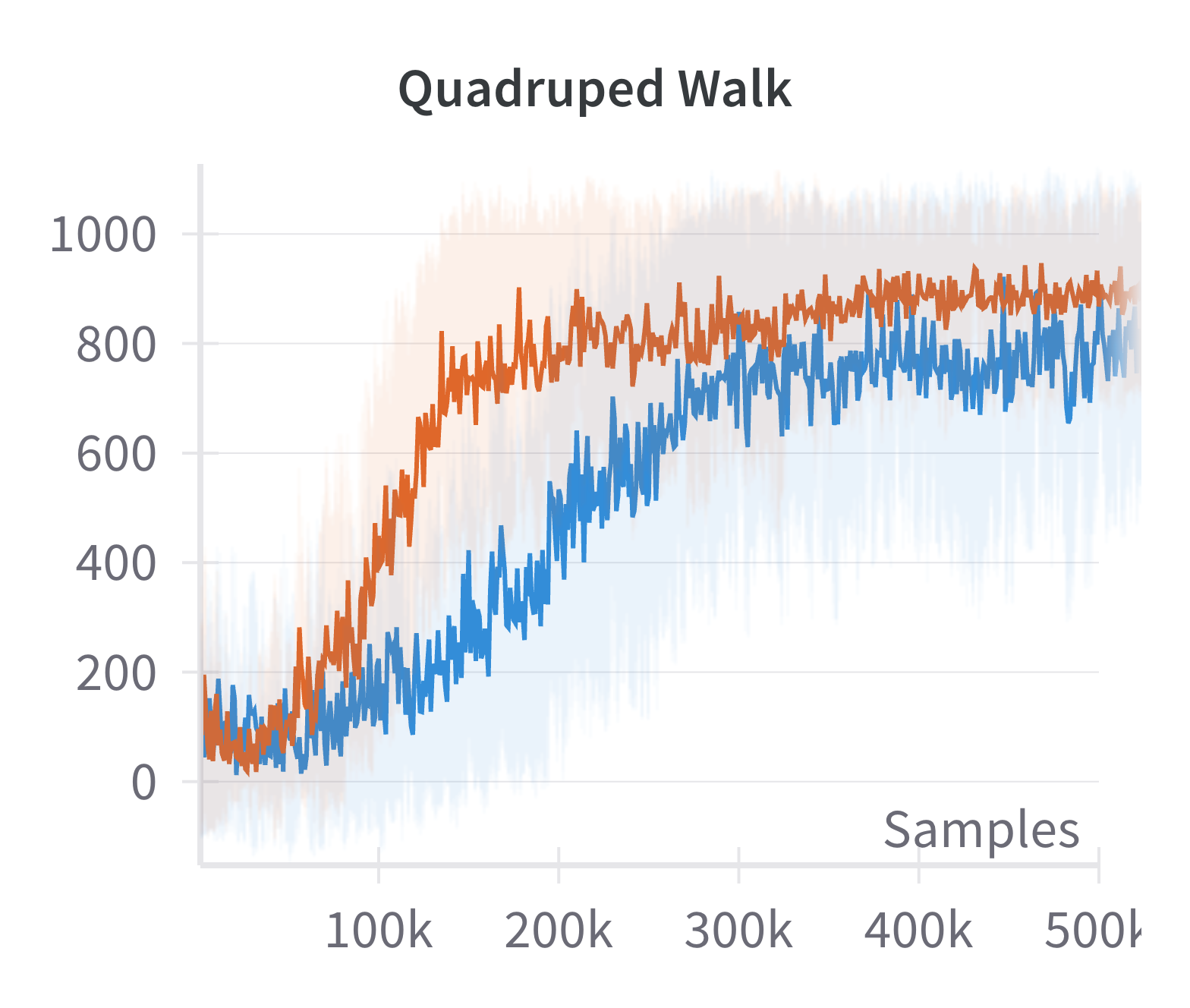
Figure 4: Discounted returns of SAC (blue) and sparse SAC (red) $\alpha_{\pi}$.

Ablation studies over the sparsification hyperparameters and computational profiling indicate that the additional computational cost is moderate and does not render the approach intractable, given the performance gains.

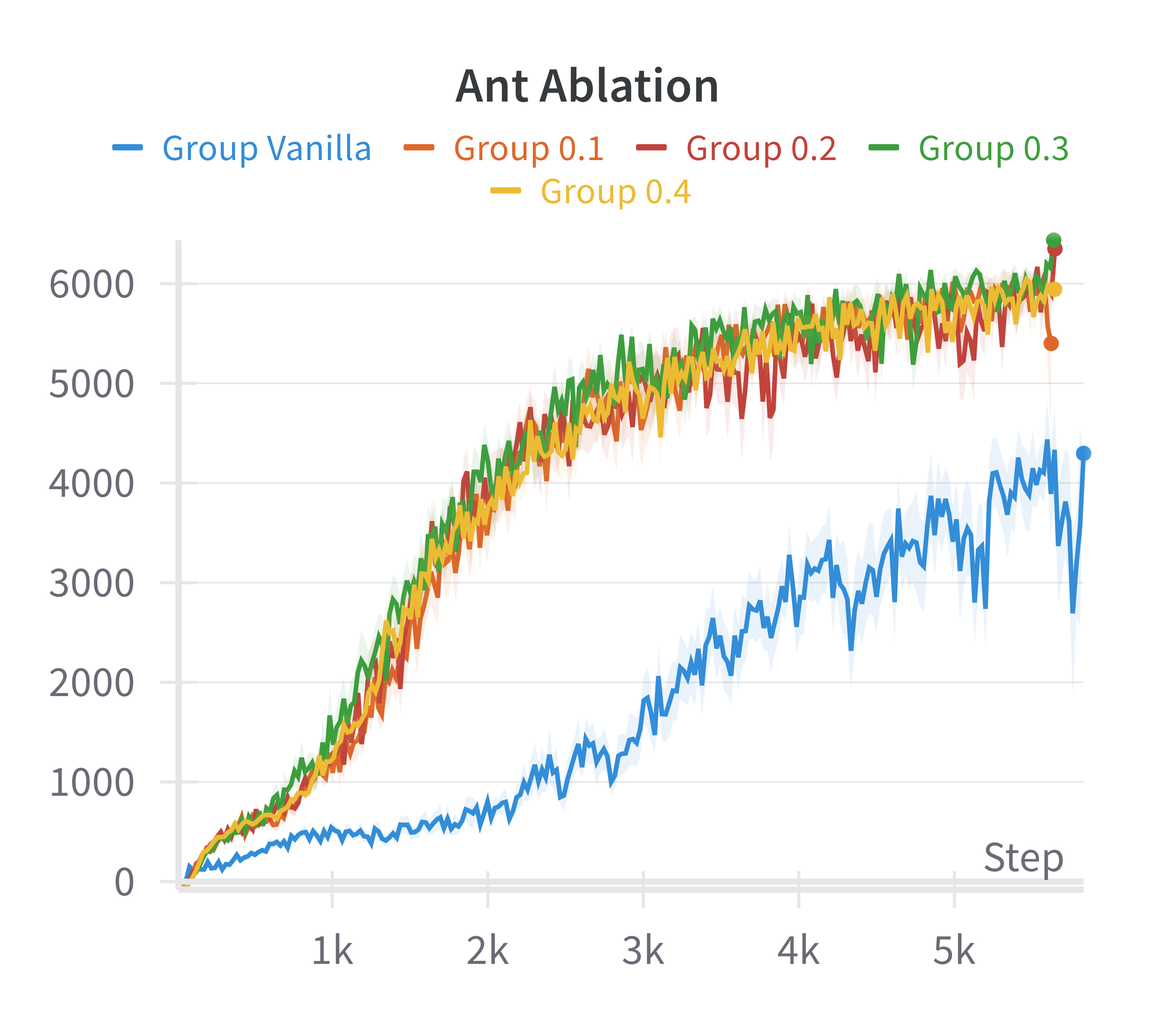
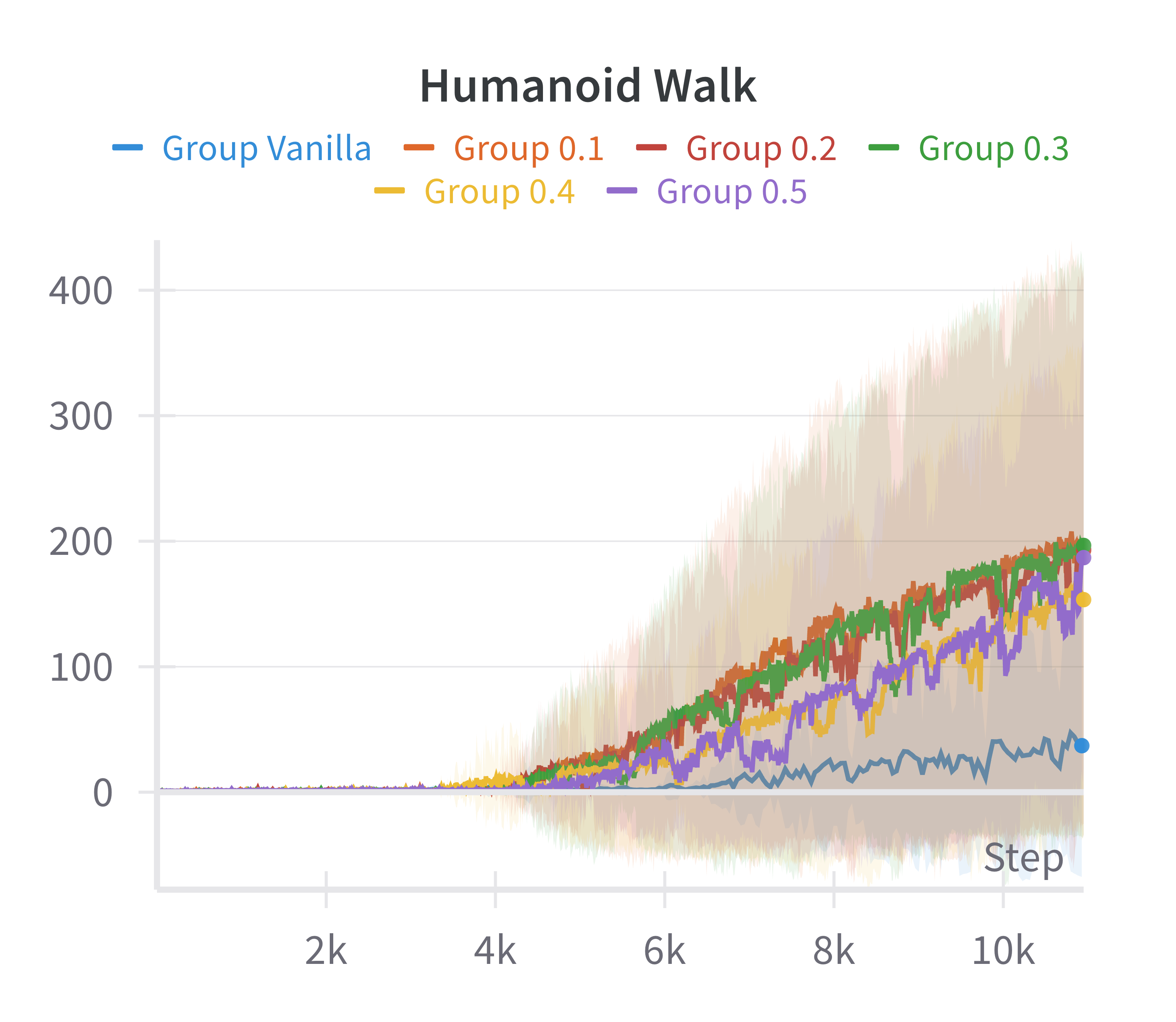
Figure 5: Ablation over the $\alpha_Q$ parameter.

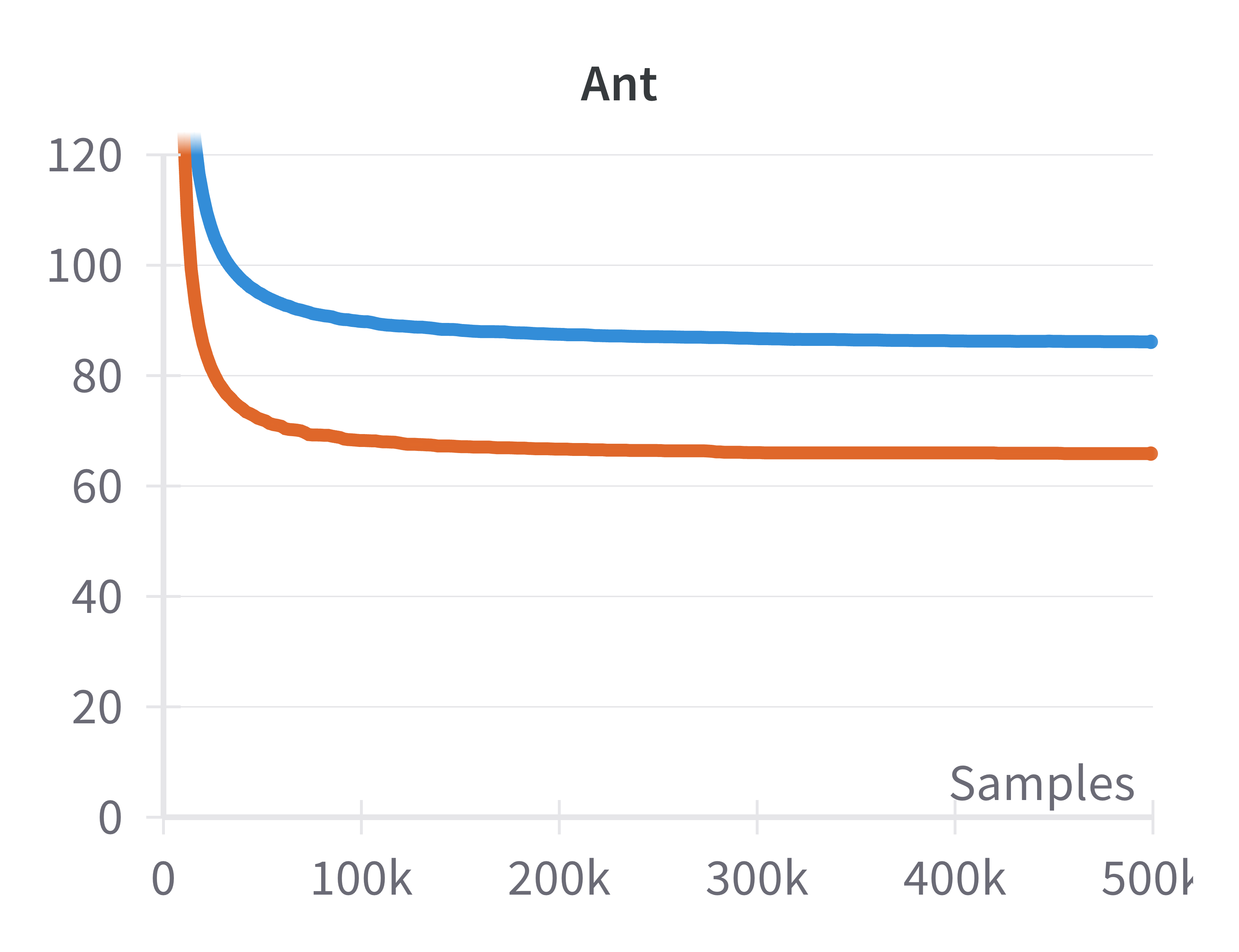
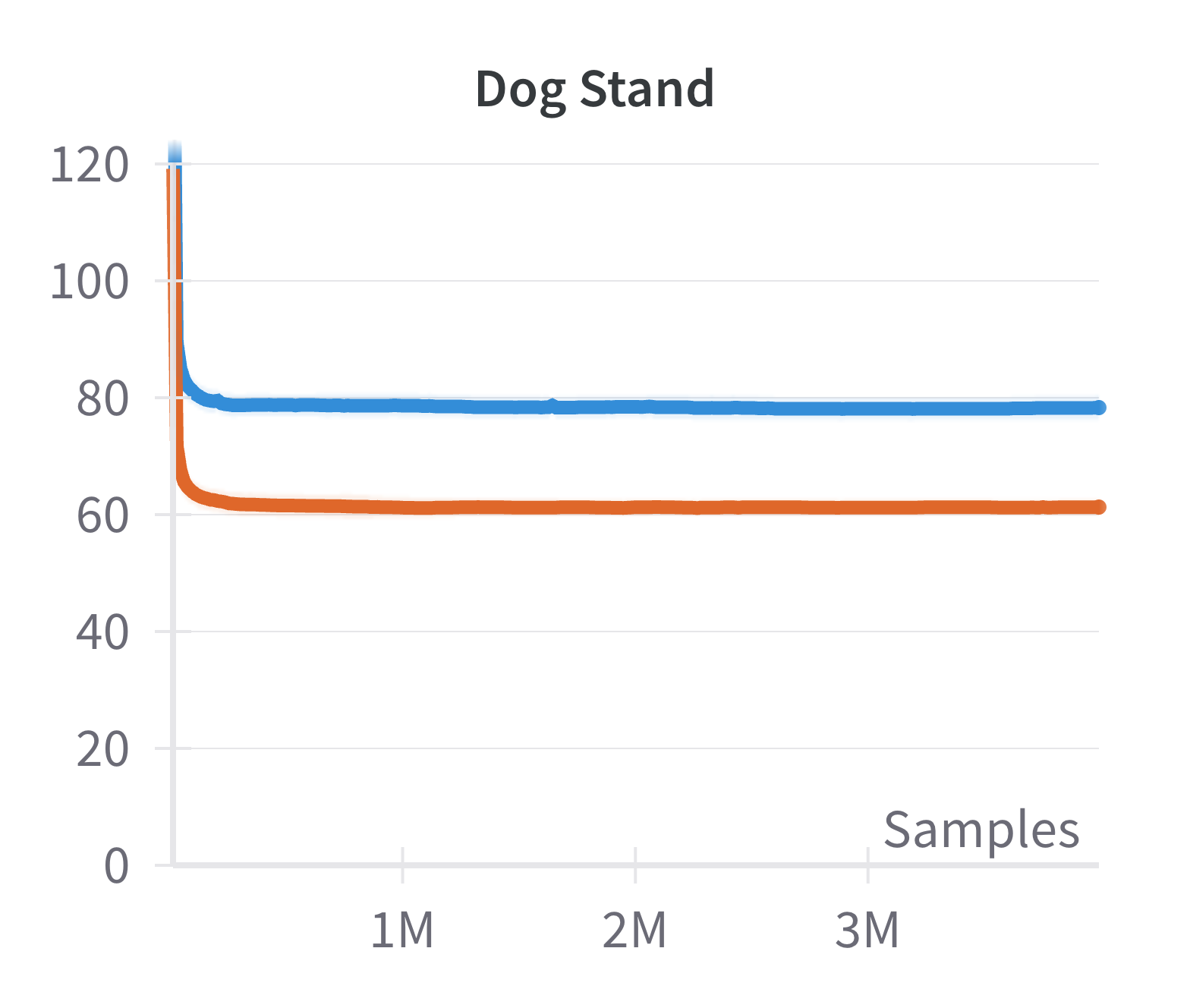
Figure 6: Steps per second for SAC (blue) and sparse SAC (red) as training progresses, showing moderate computational overhead for the sparse variant.

Theoretical and Practical Implications

The main theoretical contribution is the explicit characterization of the local geometry of attainable states under neural RL policies, with a provable upper bound on the manifold dimension that depends only on the action space. This result has several implications:

• Sample Complexity and Generalization: Since the effective complexity of the RL problem is governed by the intrinsic dimension of the attainable state manifold, rather than the ambient state space, this provides a principled explanation for the empirical success of RL in high-dimensional domains and suggests that sample complexity should scale with $d_a$ rather than $d_s$.
• Representation Learning: The findings justify the use of architectural components (e.g., sparsification layers) that promote low-dimensional, disentangled representations, as these are well-aligned with the geometry of the RL problem.
• Algorithm Design: The results motivate the development of RL algorithms and architectures that explicitly exploit the low-dimensional structure of the attainable state manifold, potentially leading to more efficient and robust learning in complex environments.

Limitations and Future Directions

The analysis is restricted to deterministic environments and assumes access to the true value function gradients, which may not hold in practical settings with stochastic transitions or function approximation errors. Extending the theory to stochastic environments, deeper architectures, and more general activation functions is a promising direction. Additionally, the impact of noise and exploration on the geometry of attainable states remains an open question.

Conclusion

This work provides a rigorous geometric characterization of the set of states attainable by neural RL agents in continuous domains, establishing that this set is concentrated on a low-dimensional manifold whose dimension is determined by the action space. The theoretical results are validated empirically and leveraged to design more effective RL architectures. These insights have significant implications for the design, analysis, and understanding of RL algorithms in high-dimensional continuous control settings, and open avenues for further research into the interplay between geometry, representation, and learning in RL.