A note on the Artstein-Avidan-Milman's generalized Legendre transforms (2507.20577v1)

Abstract: Artstein-Avidan and Milman [Annals of mathematics (2009), (169):661-674] characterized invertible reverse-ordering transforms on the space of lower-semi-continuous extended real-valued convex functions as affine deformations of the ordinary Legendre transform. In this note, we prove that all those generalized Legendre transforms on functions correspond to the ordinary Legendre transform on dually corresponding affine-deformed functions. That is, generalized convex conjugates are convex conjugates of affine-deformed functions. We conclude this note by sketching how this result can be interpreted from the lens of information geometry.

• The paper demonstrates that any generalized Legendre-Fenchel transform (GLFT) can be recast as an ordinary Legendre-Fenchel transform applied to an affine-deformed function.
• It provides an explicit, involutive mapping between affine deformation parameters, simplifying the structure and analysis of convex conjugates.
• The work links these findings to information geometry, showing that affine invariance underpins the duality and divergence measures in dually flat spaces.

Generalized Legendre Transforms as Affine-Deformed Convex Conjugates

Introduction

This note addresses the structure of generalized Legendre-Fenchel transforms (GLFTs) as introduced by Artstein-Avidan and Milman, which characterize all invertible, order-reversing transforms on the space of proper lower semi-continuous convex functions as affine deformations of the classical Legendre-Fenchel transform (LFT). The main result demonstrates that any such GLFT can be realized as an ordinary LFT applied to an affine-deformed function, thus reducing the apparent generality of GLFTs to a canonical form. The implications of this result are further interpreted through the lens of information geometry, connecting the algebraic structure of GLFTs to the geometry of dually flat spaces.

Theoretical Framework

Let $\Gamma_0$ denote the space of proper, lower semi-continuous, extended real-valued convex functions on $\mathbb{R}^m$. The classical Legendre-Fenchel transform $L$ maps $F \in \Gamma_0$ to its convex conjugate $F^*$:

$$(LF)(\eta) = \sup_{\theta \in \mathbb{R}^m} \left\{ \langle \theta, \eta \rangle - F(\theta) \right\}.$$

The Moreau-Fenchel-Rockafellar theorem ensures that for $F \in \Gamma_0$, the biconjugate $F^{**}$ recovers $F$.

Artstein-Avidan and Milman established that any invertible, order-reversing transform $T$ on $\Gamma_0$ must be of the form:

$$(TF)(\eta) = \lambda (LF)(E\eta + f) + \langle \eta, g \rangle + h,$$

where $\lambda > 0$, $E \in GL(\mathbb{R}^m)$, $f, g \in \mathbb{R}^m$, and $h \in \mathbb{R}$. This result axiomatizes the class of GLFTs.

Main Result: GLFTs as LFTs of Affine-Deformed Functions

The central contribution of the note is the explicit construction showing that any GLFT can be written as the LFT of an affine-deformed function. Specifically, for parameters $P = (\lambda, A, b, c, d)$, define the affine deformation:

$$F_P(\theta) = \lambda F(A\theta + b) + \langle \theta, c \rangle + d.$$

It is shown that $F_P \in \Gamma_0$ whenever $F \in \Gamma_0$ and $A \in GL(\mathbb{R}^m)$, and that the LFT of $F_P$ is another affine deformation of $F^*$, with parameters given by an explicit involutive mapping $P \mapsto P^\diamond$:

$$P^\diamond = \left( \lambda, \frac{1}{\lambda}A^{-1}, -\frac{1}{\lambda}A^{-1}c, -A^{-1}b, \langle b, A^{-1}c \rangle - d \right).$$

Thus,

$L(F_P) = (LF)_{P^\diamond}.$

The involutive property $({P^\diamond})^\diamond = P$ ensures that the LFT remains an involution under affine deformation.

Consequently, any GLFT $T$ can be realized as:

$(TF)(\eta) = L(F_{P^\diamond})(\eta),$

where the parameters of the affine deformation are determined by the GLFT parameters.

Figure 1: The ordinary Legendre transform on classes of functions: Relationships with representational Fenchel-Young and Bregman divergences, flat Hessian divergence, and $\alpha$-geometry in information geometry.

Examples and Structural Properties

The note provides several canonical examples of convex conjugate pairs, including affine functions, exponential functions (yielding the Shannon entropy as conjugate), and $L_p$ norms (with conjugate exponents). The structure of Legendre-type functions is discussed, emphasizing the reciprocal nature of gradients for such pairs and the importance of strict convexity and differentiability on open domains.

The reverse-ordering property of the LFT is highlighted: if $F_2 \leq F_1$, then $LF_2 \geq LF_1$, and vice versa. This property underpins the order-reversing nature of GLFTs.

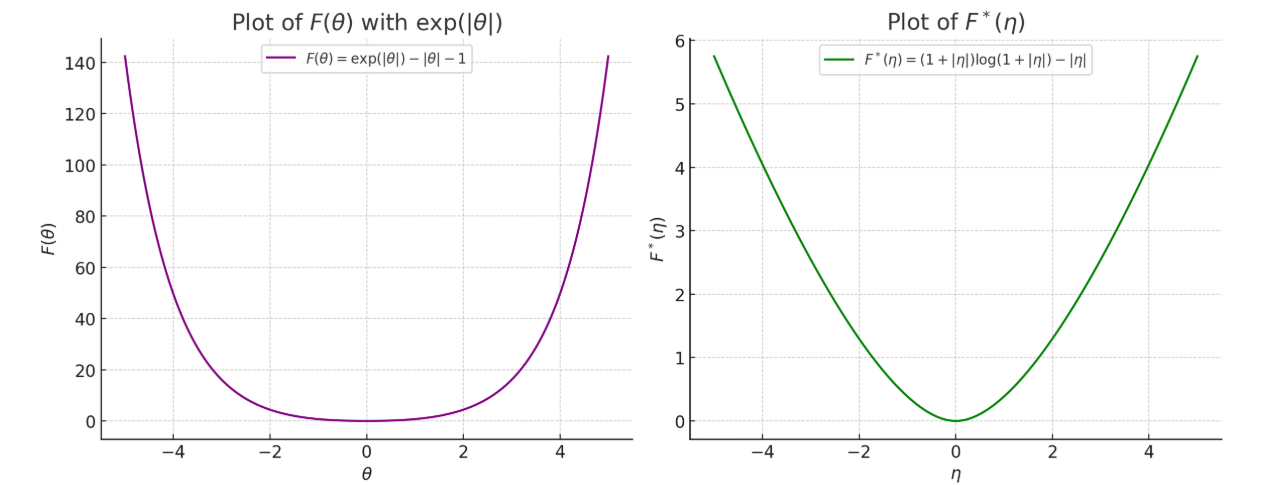
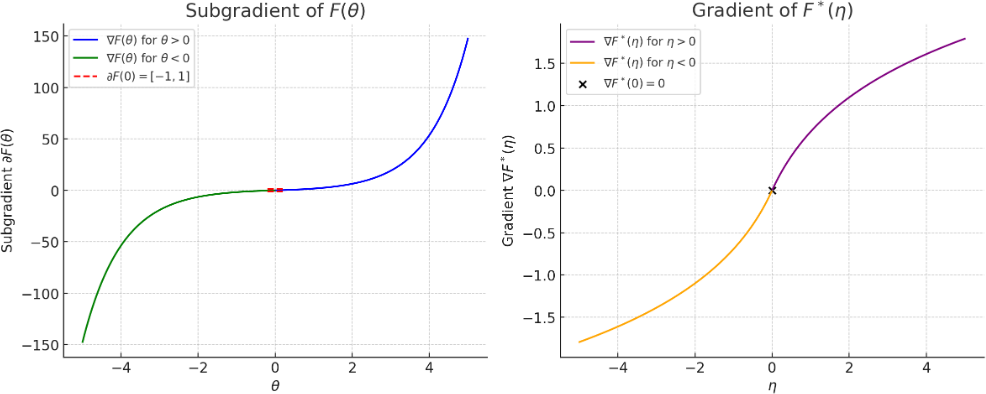
Figure 2: A pair $(F(\theta),F^*(\eta))$ of conjugate functions (top) with their subgradients plotted (bottom). $F(\theta)$ is not differentiable at $\theta=0$ and thus admits a subgradient $\partial F(0)$ at $\theta=0$. $F^*(\eta)$ is everywhere differentiable, and when $\theta \neq 0$, $\nabla F^* = (\nabla F)^{-1}$.

Information-Geometric Interpretation

The result is interpreted within the framework of information geometry, where a strictly convex function $F$ induces a dually flat manifold $(M, g, \nabla, \nabla^*)$. The affine freedom in the choice of coordinate systems and potential functions corresponds precisely to the affine deformations in the GLFT characterization. The Fenchel-Young inequality and the associated divergences (Fenchel-Young, Bregman, and dually flat divergences) are invariant under these affine transformations, up to scaling.

The equivalence relation $F \sim \tilde{F}$ if $\tilde{F} = F_P$ for some $P$ partitions $\Gamma_0$ into moduli spaces of dually flat structures, and the GLFTs correspond to isometries on these moduli spaces. The scaling parameter $\lambda$ reflects the freedom to rescale the metric and connections in the information-geometric structure.

Implications and Future Directions

The reduction of GLFTs to ordinary LFTs on affine-deformed functions clarifies the algebraic and geometric structure underlying duality in convex analysis. This result has implications for the paper of divergences, optimization, and statistical models where duality and convex conjugacy play a central role. In information geometry, it provides a rigorous foundation for the invariance of divergences and geometric structures under affine transformations.

Potential future directions include the exploration of these structures in infinite-dimensional settings, applications to statistical exponential families, and the development of algorithms that exploit the affine invariance of divergences and duality mappings.

Conclusion

This note establishes that all generalized Legendre-Fenchel transforms, as characterized by Artstein-Avidan and Milman, are equivalent to ordinary Legendre-Fenchel transforms applied to affine-deformed functions. The explicit involutive correspondence between the parameters of the affine deformation and the GLFT parameters provides a complete structural understanding of these transforms. The information-geometric interpretation further situates this result within the broader context of dually flat spaces and invariant divergences, offering a unified perspective on duality in convex analysis and geometry.