Beyond Binary Rewards: Training LMs to Reason About Their Uncertainty (2507.16806v1)

Abstract: When LMs are trained via reinforcement learning (RL) to generate natural language "reasoning chains", their performance improves on a variety of difficult question answering tasks. Today, almost all successful applications of RL for reasoning use binary reward functions that evaluate the correctness of LM outputs. Because such reward functions do not penalize guessing or low-confidence outputs, they often have the unintended side-effect of degrading calibration and increasing the rate at which LMs generate incorrect responses (or "hallucinate") in other problem domains. This paper describes RLCR (Reinforcement Learning with Calibration Rewards), an approach to training reasoning models that jointly improves accuracy and calibrated confidence estimation. During RLCR, LMs generate both predictions and numerical confidence estimates after reasoning. They are trained to optimize a reward function that augments a binary correctness score with a Brier score -- a scoring rule for confidence estimates that incentivizes calibrated prediction. We first prove that this reward function (or any analogous reward function that uses a bounded, proper scoring rule) yields models whose predictions are both accurate and well-calibrated. We next show that across diverse datasets, RLCR substantially improves calibration with no loss in accuracy, on both in-domain and out-of-domain evaluations -- outperforming both ordinary RL training and classifiers trained to assign post-hoc confidence scores. While ordinary RL hurts calibration, RLCR improves it. Finally, we demonstrate that verbalized confidence can be leveraged at test time to improve accuracy and calibration via confidence-weighted scaling methods. Our results show that explicitly optimizing for calibration can produce more generally reliable reasoning models.

• The paper proposes RLCR that integrates a Brier score-based calibration term with binary rewards to jointly optimize answer correctness and uncertainty estimation.
• The method reduces expected calibration error from 0.37 to 0.03 on HotPotQA while maintaining accuracy and improving performance on out-of-distribution tasks.
• Empirical results show that explicit uncertainty reasoning in the chain-of-thought leads to more reliable predictions and effective uncertainty-based test-time ensembling.

Reinforcement Learning with Calibration Rewards: Jointly Optimizing Reasoning Accuracy and Uncertainty in LLMs

Introduction

The paper "Beyond Binary Rewards: Training LMs to Reason About Their Uncertainty" (2507.16806) addresses a critical limitation in current reinforcement learning (RL) approaches for LLM (LM) reasoning: the use of binary correctness rewards that fail to penalize overconfident guessing and degrade calibration. The authors introduce RLCR (Reinforcement Learning with Calibration Rewards), a method that augments the standard binary reward with a Brier score-based calibration term, incentivizing models to output both accurate answers and well-calibrated confidence estimates. This essay provides a technical summary of the RLCR method, its theoretical guarantees, empirical results, and implications for the development of reliable reasoning LMs.

Motivation and Problem Formulation

Standard RL for reasoning LMs, often termed RLVR (Reinforcement Learning with Verifiable Rewards), optimizes a binary reward function that only considers answer correctness. This approach encourages models to maximize accuracy but does not distinguish between confident and unconfident predictions, nor does it penalize overconfident errors. Empirical evidence shows that RLVR-trained models become overconfident and poorly calibrated, especially in out-of-distribution (OOD) settings, increasing the risk of hallucinations and undermining trust in high-stakes applications.

The central questions addressed are:

1. Can reasoning models be optimized for both correctness and calibration?
2. Can the structure and content of reasoning chains themselves improve calibration?

RLCR: Method and Theoretical Guarantees

RLCR modifies the RL objective by requiring models to output both an answer $y$ and a verbalized confidence $q \in [0,1]$ after a reasoning chain. The reward function is:

$RLCR(y, q, y^*) = \mathbbm{1}_{y \equiv y^*} - (q - \mathbbm{1}_{y \equiv y^*})^2$

where $\mathbbm{1}_{y \equiv y^*}$ is the indicator of correctness, and the second term is the Brier score, a strictly proper scoring rule for binary outcomes.

Theoretical analysis establishes two key properties:

• Calibration Incentive: For any answer $y$, the expected reward is maximized when $q$ matches the true probability of correctness $p_y$.
• Correctness Incentive: Among all calibrated predictions, the reward is maximized by choosing the answer with the highest $p_y$.

This result holds for any bounded, proper scoring rule in place of the Brier score. Notably, unbounded scoring rules (e.g., log-loss) do not guarantee this property, as they can incentivize pathological behaviors (e.g., outputting deliberately incorrect answers with zero confidence).

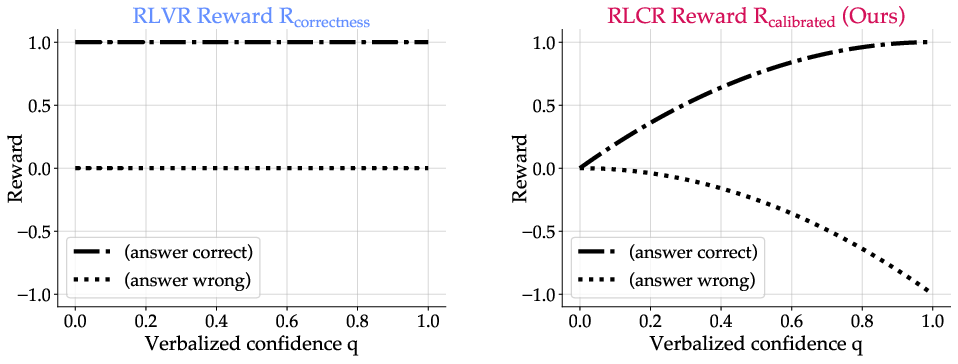
Figure 1: RLVR rewards only correctness, incentivizing guessing; RLCR jointly optimizes for correctness and calibration via a proper scoring rule.

Experimental Setup

The authors evaluate RLCR on a suite of reasoning and factual QA benchmarks, including HotPotQA, SimpleQA, TriviaQA, GPQA, Math500, GSM8K, Big-Math, and CommonsenseQA. The base model is Qwen2.5-7B, and RL is performed using GRPO with format rewards to enforce structured outputs containing > , <answer>, <analysis>, and <confidence> tags.

Baselines include:

• RLVR (binary reward)
• RLVR + post-hoc confidence classifiers (BCE and Brier loss)
• RLVR + linear probe on final-layer embeddings
• RLVR + answer token probability
• RLCR (proposed)

Evaluation metrics are accuracy, AUROC, Brier score, and Expected Calibration Error (ECE).

Empirical Results

In-Domain and Out-of-Domain Calibration

RLCR matches RLVR in accuracy but substantially improves calibration on both in-domain and OOD tasks. On HotPotQA, RLCR reduces ECE from 0.37 (RLVR) to 0.03 and Brier score from 0.37 to 0.21, with no loss in accuracy. On OOD datasets, RLVR degrades calibration relative to the base model, while RLCR improves it, outperforming all baselines, including post-hoc classifiers.

Figure 2: (a) Example RLCR reasoning chain with explicit uncertainty analysis and confidence; (b) RLCR improves in-domain accuracy and calibration over RLVR and classifier baselines; (c) RLCR generalizes better to OOD tasks, improving both accuracy and calibration.

(Table: HotPotQA and OOD results)

Method	HotPotQA Acc.	HotPotQA ECE	OOD Acc.	OOD ECE
Base	39.7%	0.53	53.3%	0.40
RLVR	63.0%	0.37	53.9%	0.46
RLVR + BCE Classifier	63.0%	0.07	53.9%	0.24
RLCR (ours)	62.1%	0.03	56.2%	0.21

RLCR also demonstrates improved calibration on mathematical reasoning tasks (Big-Math, GSM8K, Math500), with SFT+RLCR achieving the best calibration but at some cost to OOD accuracy, likely due to catastrophic forgetting.

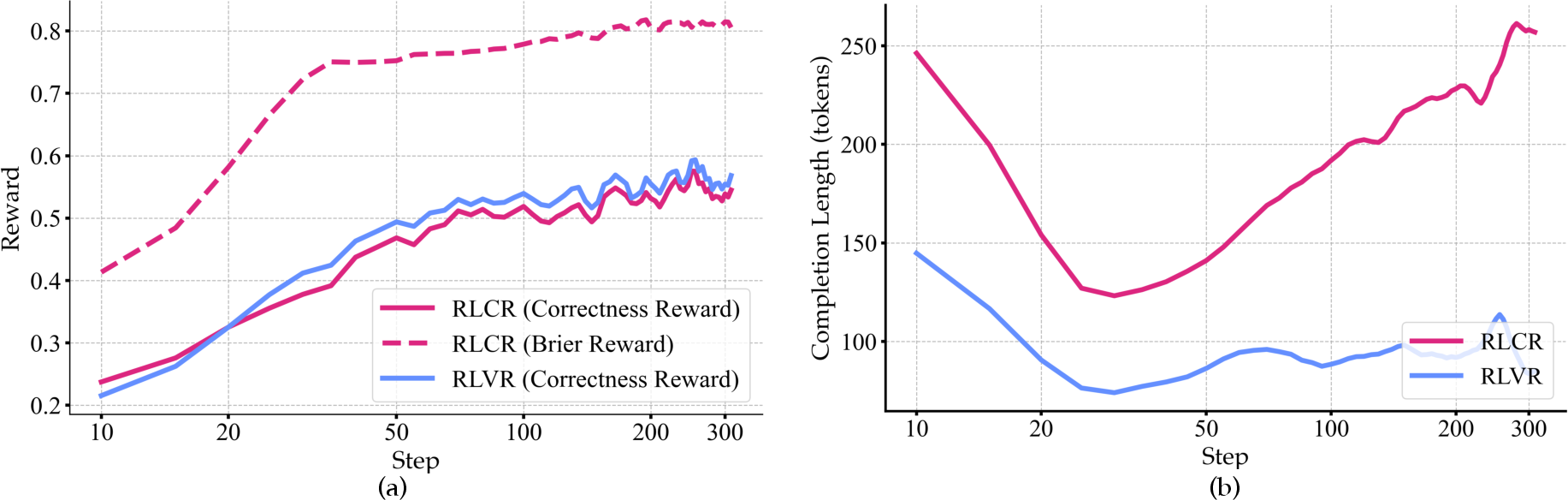
Figure 3: (a) RLCR improves both correctness and calibration rewards during training; (b) RLCR increases completion lengths, indicating more thorough uncertainty reasoning.

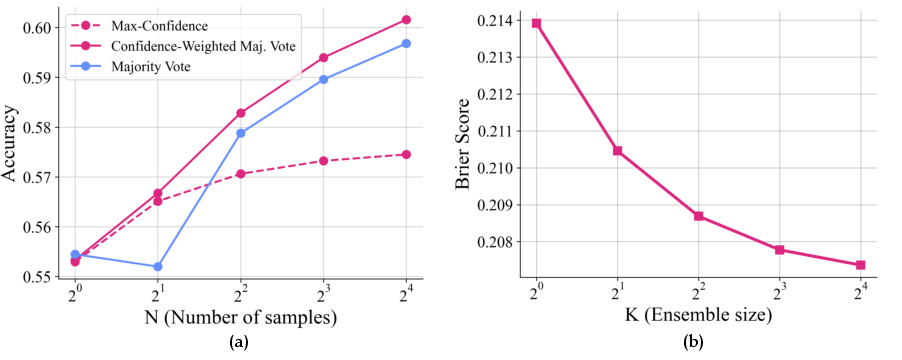
Test-Time Scaling with Verbalized Confidence

RLCR enables new test-time scaling strategies by leveraging verbalized confidence:

• Confidence-weighted majority vote outperforms vanilla majority vote and max-confidence selection, especially as the number of samples increases.
• Ensembling multiple uncertainty analyses for a fixed answer further reduces Brier score, improving calibration with minimal computational overhead.

  Figure 4: (a) Accuracy improves with sample size; confidence-weighted voting is superior. (b) Brier score decreases with ensemble size, showing improved calibration via analysis ensembling.

Role of Reasoning Chains in Calibration

Analysis classifiers trained on RLCR-generated reasoning chains outperform those trained on RLVR outputs, especially at smaller model sizes, indicating that explicit uncertainty reasoning in the chain-of-thought is essential for calibration when model capacity is limited.

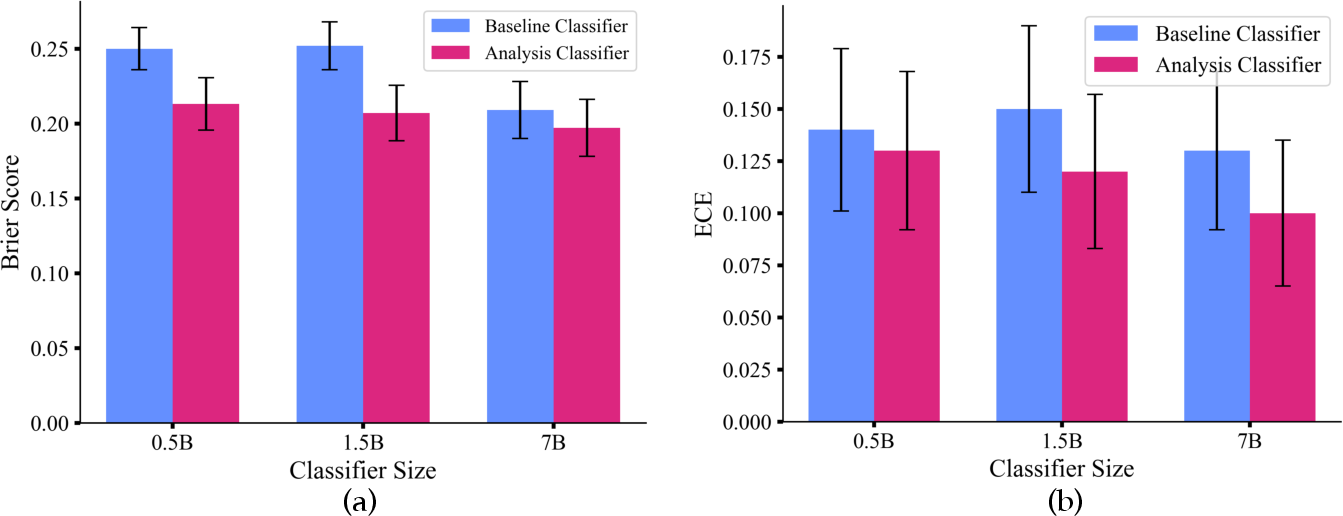
Figure 5: Analysis classifiers using RLCR chains achieve lower Brier and ECE scores at small model sizes, highlighting the value of explicit uncertainty reasoning.

Consistency of Verbalized Confidence

RLCR-trained models exhibit low intra-solution variance in confidence estimates for the same answer, indicating self-consistency. However, in OOD settings, models remain somewhat overconfident, with the sum of confidences for mutually exclusive answers exceeding 1, though RLCR is closer to the ideal than RLVR.

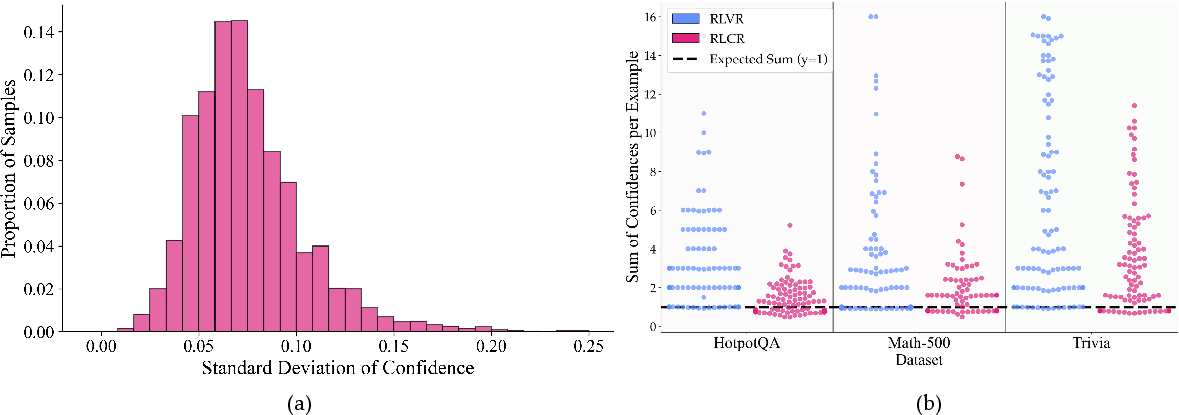
Figure 6: (a) Most samples have low standard deviation in confidence across chains; (b) RLCR's confidence sums are closer to 1, but overconfidence persists OOD.

Implementation Considerations

• Prompt Engineering: RLCR relies on structured prompts with explicit tags for reasoning, answer, analysis, and confidence. Format rewards are critical for ensuring adherence.
• Reward Design: The calibration term must use a bounded, proper scoring rule (e.g., Brier score) to guarantee joint optimization of accuracy and calibration.
• Training Dynamics: RLCR requires the model to adapt its confidence analysis as task performance improves, potentially leading to more robust generalization.
• Resource Requirements: RLCR does not require additional models or classifiers at inference, unlike post-hoc calibration methods, making it efficient for deployment.
• Test-Time Scaling: Confidence-weighted ensembling and analysis resampling are lightweight and can be applied without retraining.

Implications and Future Directions

RLCR demonstrates that reasoning LMs can be trained to output both accurate answers and well-calibrated confidence estimates, improving reliability in both in-domain and OOD settings. The method is simple to implement, theoretically grounded, and empirically effective. However, absolute calibration error remains high OOD, and models can still be overconfident in mutually exclusive settings, indicating room for further improvement.

Potential future directions include:

• Improved Calibration Objectives: Exploring alternative bounded proper scoring rules or multi-class extensions.
• Uncertainty-Aware Reasoning Chains: Further integrating uncertainty analysis into the reasoning process, possibly with explicit abstention or selective prediction mechanisms.
• Scaling to Larger Models and Tasks: Evaluating RLCR on larger LMs and more complex, open-ended tasks.
• Interpretable Uncertainty: Enhancing the interpretability and faithfulness of uncertainty analyses in chain-of-thought reasoning.

Conclusion

RLCR provides a principled and practical approach to training reasoning LMs that are both accurate and well-calibrated. By augmenting the RL objective with a proper scoring rule, models learn to reason about their own uncertainty, yielding more reliable predictions and enabling new test-time scaling strategies. While challenges remain in achieving perfect calibration, especially OOD, RLCR represents a significant step toward trustworthy, uncertainty-aware LLM reasoning.