- The paper introduces a novel row-sparse update and Sparse State Expansion to efficiently scale linear attention without increasing parameter count.
- It reinterprets key vector mapping as a classification task, reducing interference and extending receptive fields for improved token-level information retention.
- Empirical results demonstrate superior performance in language modeling, retrieval, and mathematical reasoning, with SSE-H achieving state-of-the-art benchmarks.
Scaling Linear Attention with Sparse State Expansion: A Technical Analysis
Introduction and Motivation
The Transformer architecture, while highly effective for sequence modeling, is fundamentally limited by its quadratic computational complexity and linear memory growth with respect to sequence length. Linear attention variants have emerged to address these bottlenecks by compressing context into fixed-size states, enabling sub-quadratic complexity and constant memory usage during inference. However, these approaches often suffer from degraded performance in tasks requiring fine-grained token-level information, such as in-context retrieval and mathematical reasoning, due to aggressive contextual compression.
This paper introduces two principal innovations to address these limitations: (1) a row-sparse update formulation for linear attention, conceptualizing state updating as an information classification problem, and (2) Sparse State Expansion (SSE), which expands the contextual state into multiple partitions, decoupling parameter size from state capacity while maintaining the sparse classification paradigm. The proposed methods are validated across LLMing, retrieval, and reasoning benchmarks, demonstrating strong empirical performance and favorable scaling properties.
The core insight is to reinterpret the key vector mapping in linear attention as a classification function, where each state row corresponds to a distinct class. In this framework, the key vector kt is produced by a classifier (e.g., a linear or nonlinear transformation of the input), and the state update is performed selectively on rows corresponding to the top-k predicted classes via a softmax-based hard classification.
This approach yields several benefits:
Empirical analysis of row-wise cosine similarity matrices demonstrates that more expressive classification functions (e.g., softmax-based hard classifiers) yield lower inter-row similarity, indicating more effective information separation.

Figure 2: Row-wise cosine similarity matrices show that softmax-based hard classification achieves lower inter-row similarity, reflecting more effective information separation.
Sparse State Expansion (SSE): Decoupling State and Parameter Size
A critical limitation of linear attention is the restricted memory capacity imposed by small state sizes. SSE addresses this by expanding the state into N partitions, each managed by shared attention parameters. Partition selection is performed via a learnable bias, followed by softmax-based row selection within the chosen partitions. This design achieves:
- Parameter-State Decoupling: State capacity can be scaled independently of parameter count, enabling larger effective memory without increasing model size.
- Sparse Classification: The top-k selection mechanism ensures that only a subset of partitions and rows are updated per token, maintaining computational efficiency.
- Enhanced State Diversity: SSE states exhibit higher singular value entropy and lower inter-partition similarity, indicating more diverse and less compressible state compositions.
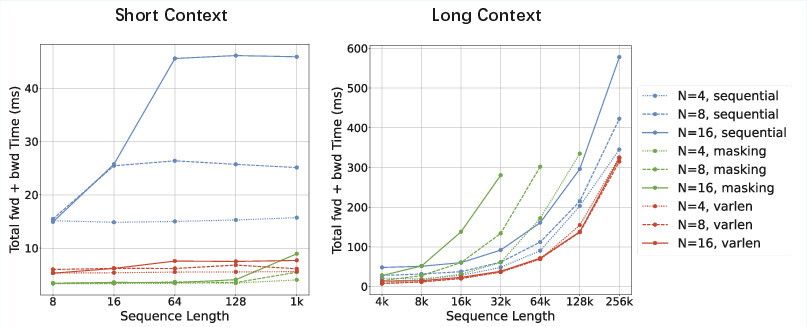
Efficient Implementation of SSE
SSE is implemented with two strategies to maximize hardware efficiency:
These implementations ensure that SSE scales favorably with respect to both sequence length and state size, supporting efficient training and inference on modern hardware.
Empirical Results
LLMing and Retrieval
SSE demonstrates strong LLMing performance, outperforming or matching advanced linear attention models and approaching Transformer-level accuracy in hybrid configurations. In retrieval-intensive tasks, SSE consistently outperforms other linear attention models, with the hybrid SSE-H variant narrowing the gap with softmax attention Transformers.
Mathematical Reasoning
A notable result is the performance of the 2B SSE-H model, which achieves 64.7 on AIME24 and 51.3 on AIME25, significantly surpassing similarly sized open-source Transformers. This establishes SSE-H as a state-of-the-art small reasoning model.
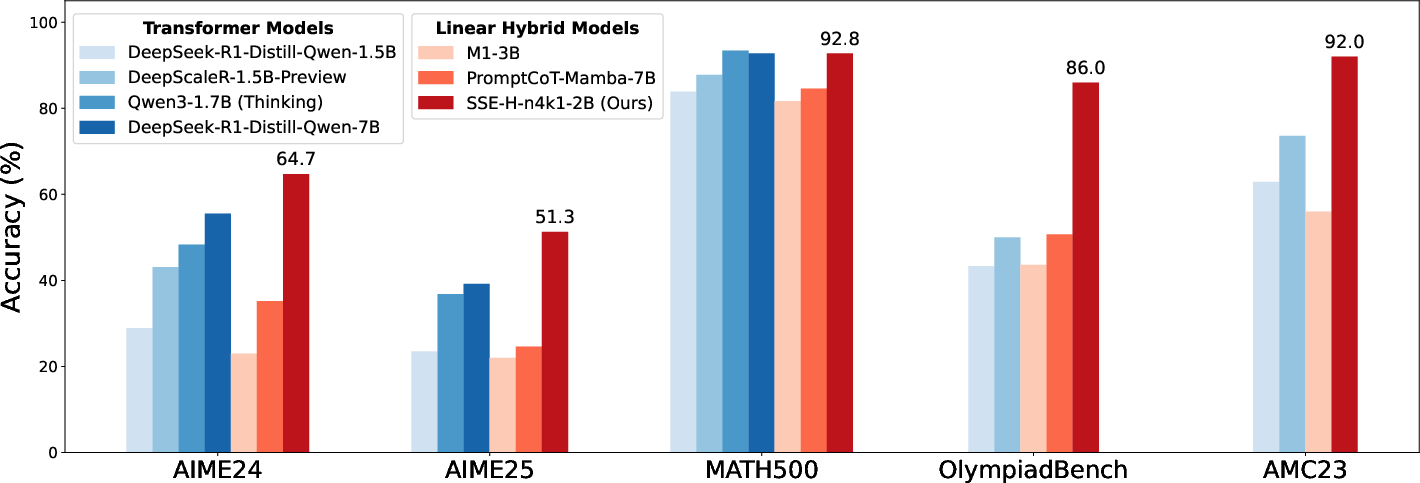
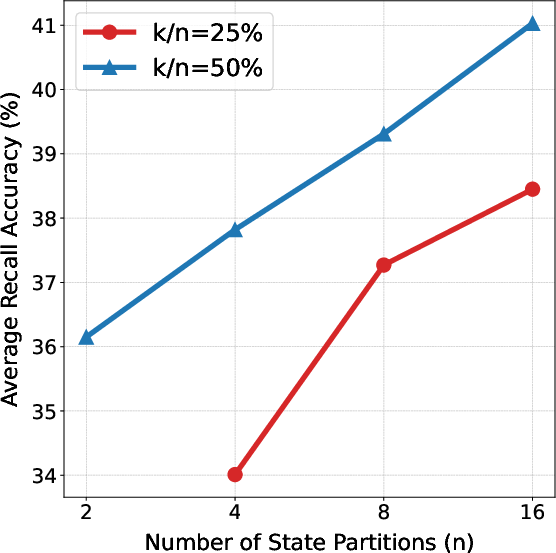
Figure 4: Left: SSE-H achieves superior mathematical reasoning performance compared to similarly sized Transformers. Right: Recall performance scales with the number of state partitions n and top-k selection size k.
State Scaling and Recall
SSE exhibits monotonic improvements in recall performance with increasing state size, without increasing parameter count. The recall benefit saturates beyond a certain sparsity ratio, and the method allows for flexible scaling via up-training.
Top-k row-sparse updates lead to longer effective context and more accurate information storage, as shown in synthetic MQAR experiments.
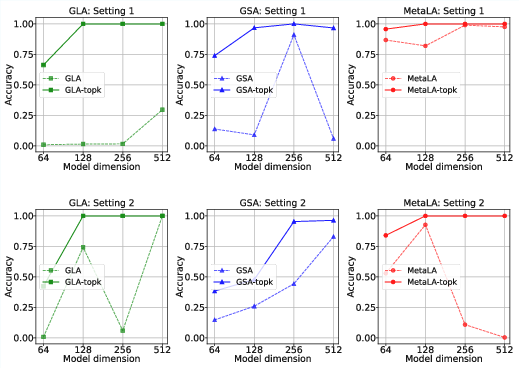
Figure 5: Top-k row-sparse updates yield longer effective context and more accurate information storage, with recall performance increasing monotonically with state size.
SSE also achieves consistently larger receptive fields than GLA across all layers, confirming its enhanced capacity for long-range information integration.
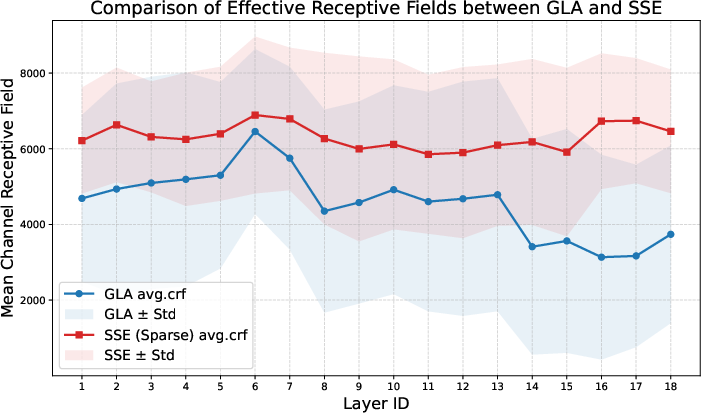
Figure 6: SSE exhibits broader receptive fields than GLA across all layers, supporting improved long-range information access.
Theoretical and Practical Implications
The row-sparse update and SSE framework provide a principled approach to context compression in linear attention models, balancing modeling fidelity and computational efficiency. The information classification perspective unifies and extends prior work on state expansion and mixture-of-experts memory, offering a generalizable mechanism for scalable memory management.
Practically, SSE enables efficient long-context modeling with minimal parameter overhead, supporting both pure linear and hybrid architectures. The method is compatible with up-training and conversion from pretrained Transformers, facilitating flexible deployment across diverse model architectures and training regimes.
Limitations and Future Directions
The current SSE design is most effective with diagonal gating mechanisms; integration with more complex state transition matrices (e.g., delta-rule mechanisms) remains challenging. Further research into state-aware classifiers and context/history-dependent partition selection is warranted. Additionally, optimizing the search for partition count and sparsity ratio, potentially via up-training, is a promising direction for future work.
Conclusion
This work introduces a row-sparse update formulation and Sparse State Expansion (SSE) for linear attention, conceptualizing state updates as an information classification process and enabling efficient, scalable memory capacity. SSE and its hybrid variant achieve superior performance across LLMing, retrieval, and mathematical reasoning tasks, with strong empirical and theoretical support for their effectiveness. The framework offers a robust foundation for future research in efficient long-context modeling and scalable sequence architectures.