Estimating causal distances with non-causal ones (2506.22421v1)

Abstract: The adapted Wasserstein ($AW$) distance refines the classical Wasserstein ($W$) distance by incorporating the temporal structure of stochastic processes. This makes the $AW$-distance well-suited as a robust distance for many dynamic stochastic optimization problems where the classical $W$-distance fails. However, estimating the $AW$-distance is a notably challenging task, compared to the classical $W$-distance. In the present work, we build a sharp estimate for the $AW$-distance in terms of the $W$-distance, for smooth measures. This reduces estimating the $AW$-distance to estimating the $W$-distance, where many well-established classical results can be leveraged. As an application, we prove a fast convergence rate of the kernel-based empirical estimator under the $AW$-distance, which approaches the Monte-Carlo rate ($n^{-1/2}$) in the regime of highly regular densities. These results are accomplished by deriving a sharp bi-Lipschitz estimate of the adapted total variation distance by the classical total variation distance.

• The paper proposes a bi-Lipschitz estimate linking adapted Wasserstein distance to classical Wasserstein distance using probability measures with Sobolev regularity.
• The methodology employs kernel-based empirical estimators that achieve fast convergence rates, approaching Monte Carlo efficiency for smooth densities.
• The results enhance computational efficiency in stochastic control by translating complex causal distance estimations into tractable non-causal measures.

Estimating Causal Distances with Non-Causal Ones

Introduction

The adapted Wasserstein ($AW$) distance is a refined measure derived from the classical Wasserstein ($W$) distance, tailored to incorporate the temporal structure of stochastic processes. This paper establishes a framework to estimate the $AW$ distance using the $W$ distance, which simplifies the problem of estimating $AW$ distances by leveraging existing results in $W$ distances. This is accomplished by proving a bi-Lipschitz estimate for the adapted total variation distance in terms of the classical total variation distance, particularly useful in dynamic stochastic optimization problems where the temporal flow of information is a critical factor.

Main Contributions

This work focuses on bounding adapted Wasserstein distances using non-adapted Wasserstein distances under the presence of regularity properties in the underlying probability measures. The essential technical contribution involves deriving upper bounds for the $AW$ distance from above using the classical $W$ distance, considering measures with Sobolev regularity. Specifically, the paper establishes that for probability measures with Sobolev densities of order $k$, $AW_1(\mu,\nu)$ can be bounded above by $W_1(\mu,\nu)^{\frac{k}{k+1}}$, and asserts that this exponent is sharp.

Key Results:

• Bi-Lipschitz Estimate: The relation $AW_1(\mu,\nu)\lesssim W_1^{\frac{k}{k+1}}(\mu,\nu)$ offers a pathway to reduce complex estimation challenges of $AW$ distances to the more manageable $W$ distances.
• Fast Convergence Rates: For smooth densities, they achieve convergence rates of adapted empirical approximations that approach the Monte Carlo rate as the smoothness increases. This implies that increasing the level of smoothness in the measures aids significantly in the fast convergence of these estimations.

Estimation Insights

The established inequalities for the adapted and classical Wasserstein distances enable leveraging classical results available for $W$ distances. Below are some of the core aspects of these translations:

• Empirical Density Estimation: A robust technique employed is the use of kernel-based empirical estimators, where the convergence rate is closely tied to the smoothness of the underlying density. This results in the approximation’s convergence to follow a minimax-optimal framework, achieving high accuracy with sufficient sample data.
• Computational Efficiency: By reducing the complexity of computing $AW$ distances to $W$ distances, practitioners can use well-optimized computational routines available for $W$ distances, potentially enhancing both the speed and accuracy of stochastic control solutions in finance and economics.

Theoretical and Practical Implications

From a theoretical perspective, the sharp bounds and convergence rates provide new avenues for analyzing stochastic processes while ensuring robustness and precision. Practically, these results can significantly impact fields like mathematical finance, where decision-making under uncertainty requires precise and computationally feasible distance measures between stochastic models.

Moreover, the paper challenges initial assumptions about the difficulty of estimating $AW$ distances by offering an innovative way to circumvent computational bottlenecks through well-understood methodologies employed in the field of $W$ distances.

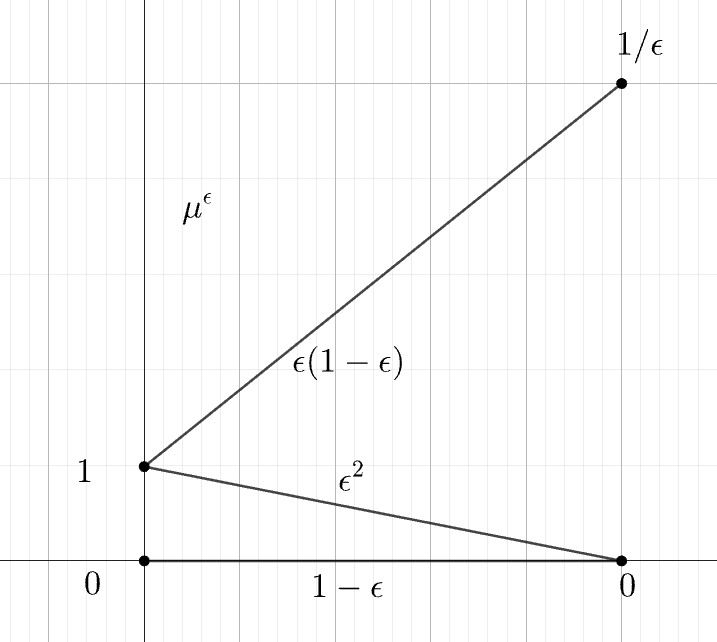
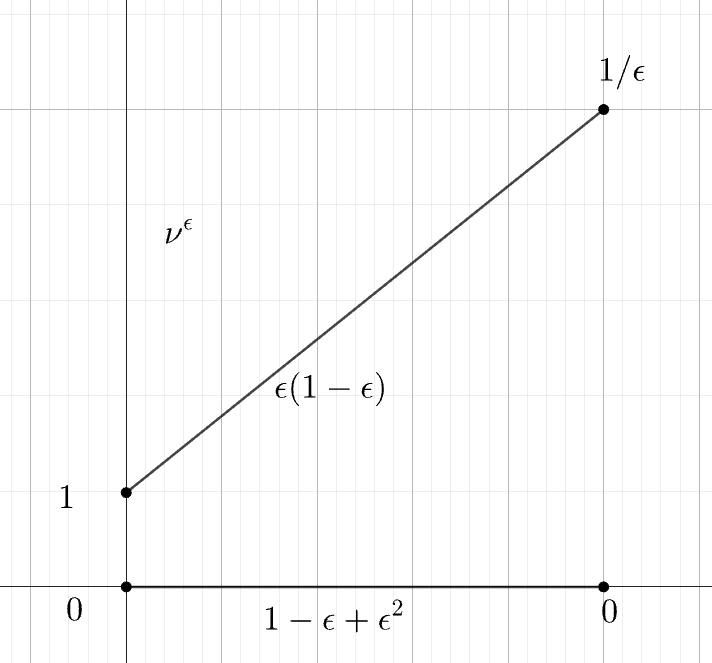
Figure 1: Demonstrates the density representation facilitating the estimate relationship $$AW_1(\mu,\nu) \lesssim W_1^{\frac{k}{k+1}}(\mu,\nu)$$.

Conclusion

The work provides an efficient methodological change by demonstrating how non-causal distance measures can substantially assist in estimating otherwise complex causal distances. The elegance of leveraging established mathematical results to open up new practical methodologies underscores the potential for further exploration in adaptive process modeling. Future advancements will likely expand upon these results to explore further dynamic systems with increasing dimensionality and stochastic complexities.