Faithful Group Shapley Value (2505.19013v1)

Abstract: Data Shapley is an important tool for data valuation, which quantifies the contribution of individual data points to machine learning models. In practice, group-level data valuation is desirable when data providers contribute data in batch. However, we identify that existing group-level extensions of Data Shapley are vulnerable to shell company attacks, where strategic group splitting can unfairly inflate valuations. We propose Faithful Group Shapley Value (FGSV) that uniquely defends against such attacks. Building on original mathematical insights, we develop a provably fast and accurate approximation algorithm for computing FGSV. Empirical experiments demonstrate that our algorithm significantly outperforms state-of-the-art methods in computational efficiency and approximation accuracy, while ensuring faithful group-level valuation.

• The paper introduces a Faithful Group Shapley Value (FGSV) that overcomes strategic subgroup manipulation and provides fair group data valuation.
• It presents a fast approximation algorithm leveraging dominant terms to ensure computational efficiency and accuracy in valuation metrics.
• The approach is validated through applications in copyright attribution in generative AI and explainable AI for stable and consistent interpretations.

Faithful Group Shapley Value: A Detailed Analysis

Overview

This paper introduces the Faithful Group Shapley Value (FGSV) to address vulnerabilities in existing group data valuation methods, particularly the susceptibility to shell company attacks. By refining the foundational cooperative game theory-based Shapley value, this research proposes a novel framework that maintains fair compensation even when groups engage in strategic splitting. The authors present both theoretical insights and a computationally efficient approximation algorithm that ensures faithful group-level valuation.

Motivation and Problem Statement

The Shapley value is a pivotal concept for data valuation, providing fair compensation by evaluating individual data contributions to machine learning models. While individual-level Shapley values are powerful, group-level evaluations are more practical in scenarios where data is contributed in batches, such as data marketplaces or collaborative intelligence.

Existing group-level extensions of the Shapley value, such as Group Shapley Value (GSV), fail under strategic manipulation, notably the shell company attack. In this attack, groups unjustly inflate valuations by dividing data into smaller subgroups, thereby altering the fairness of valuations. FGSV is introduced to counter this drawback by ensuring valuations remain consistent regardless of group partitioning.

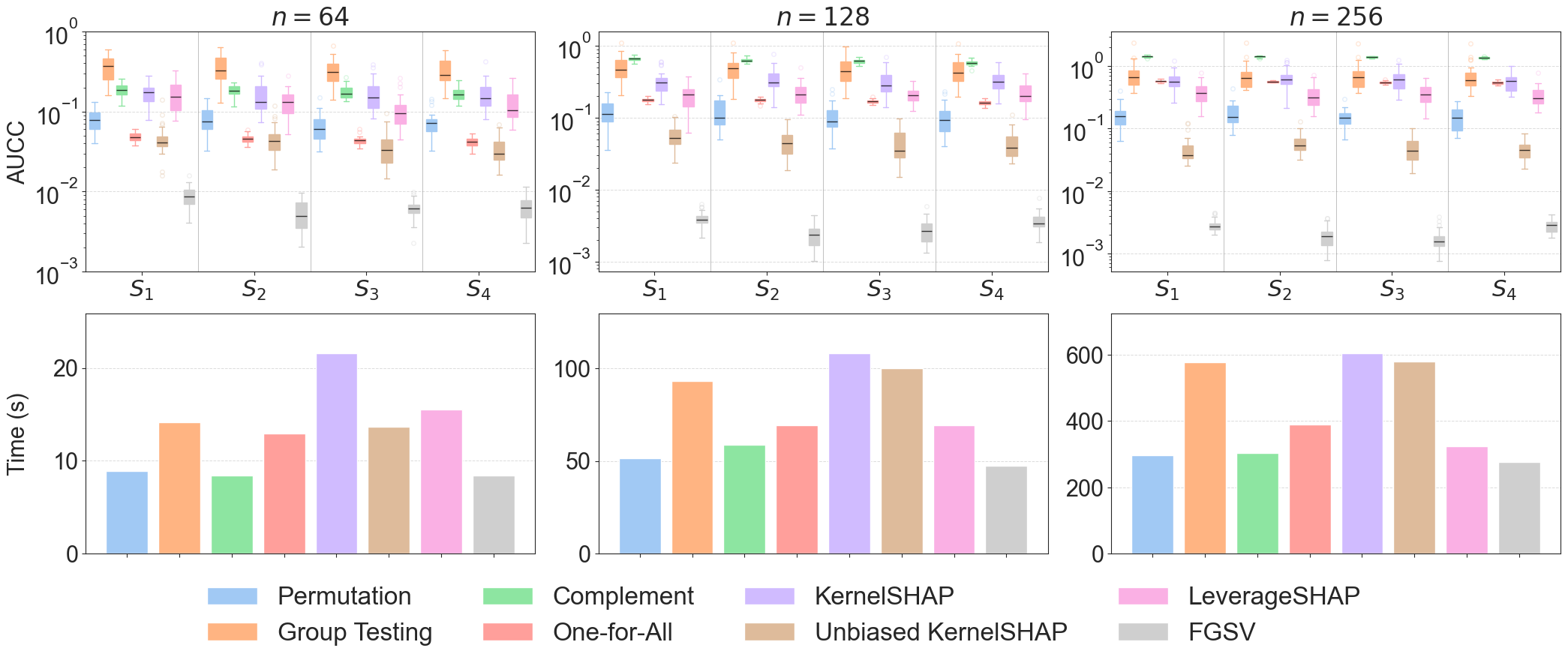
Figure 1: Performance comparison in the SOU game. Top: Our method (FGSV) achieves the lowest AUCC across all problem sizes. Bottom: Our method costs the lowest runtime per iteration.

The Faithful Group Shapley Value

Theoretical Foundation

FGSV is built upon a set of axioms designed for faithful group data valuation, which includes symmetry, linearity, efficiency, and a newly proposed faithfulness axiom. This faithfulness axiom ensures that the total value of a dataset does not change due to arbitrary subdivision of other groups.

The FGSV's value for a group is derived by summing the individual Shapley values of its members:

$FGSV(S_0) := \sum_{i \in S_0} SV(i)$

This approach uniquely satisfies all the aforementioned axioms, thus offering a robust alternative to the conventional GSV.

Algorithmic Approach

To compute FGSV, the authors propose a provably fast approximation algorithm. A key insight is that a small subset of terms dominates the FGSV formula, enabling the development of an efficient algorithm:

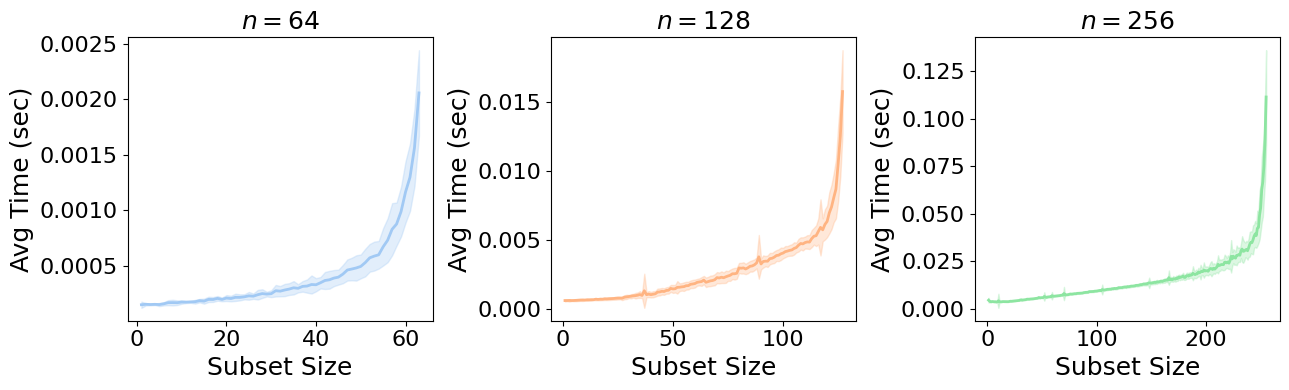
Figure 2: Empirical average runtime (in seconds) of U(S) evaluation as a function of subset size s=|S|. Each curve represents the mean over 50 randomly sampled subsets of size s; shaded areas indicate pm1 standard deviation.

Experimental Evaluation

Approximation and Computational Efficiency

Empirical trials on the Sum-of-Unanimity (SOU) game reveal that FGSV surpasses state-of-the-art methods in terms of computational efficiency and approximation accuracy. The SOU game, which contains closed-form individual Shapley values, serves as a benchmark for validating the efficiency of FGSV.

Practical Applications

Copyright Attribution in Generative AI

In generative AI, FGSV allows for fair copyright attribution by mitigating disproportionate value gains from shell company attacks. The paper demonstrates how FGSV maintains stable valuations even when strategic subgrouping is employed, thus ensuring equitable compensation.

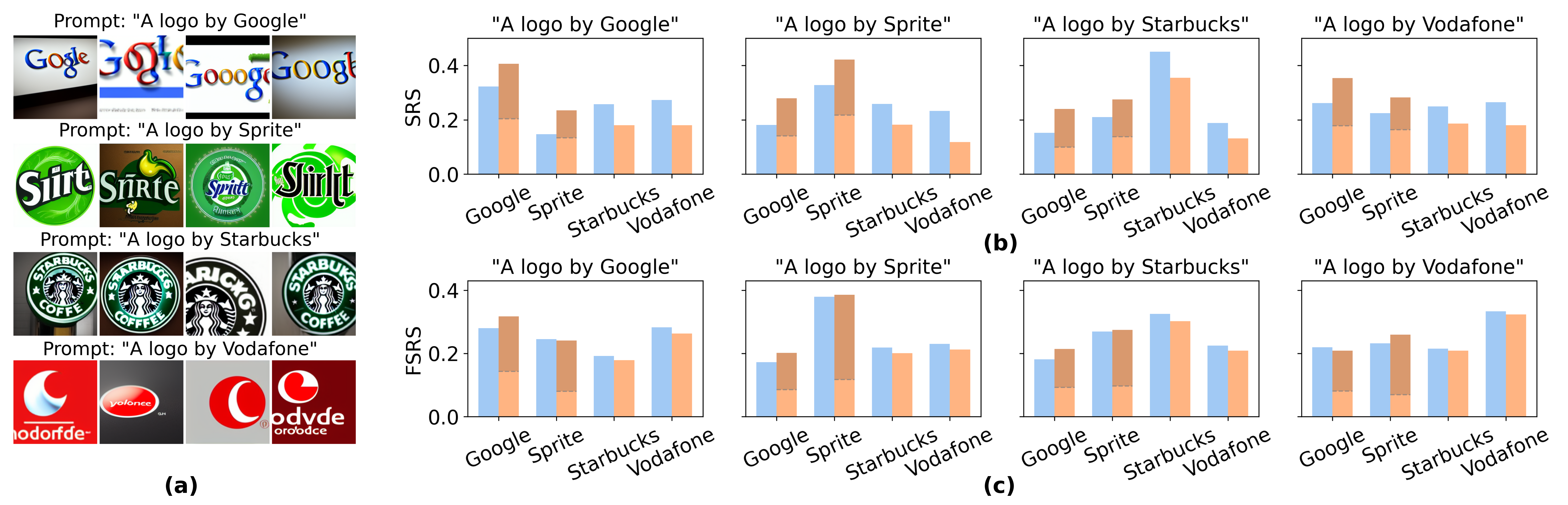
Figure 3: Comparison of SRS and FSRS for copyright attribution. (a) Example images generated using brand prompts.

Explainable AI

FGSV's robustness also extends to explainable AI, where it offers consistent category-level attributions across varying group configurations. This reliability is crucial for generating stable and interpretable insights in AI applications.

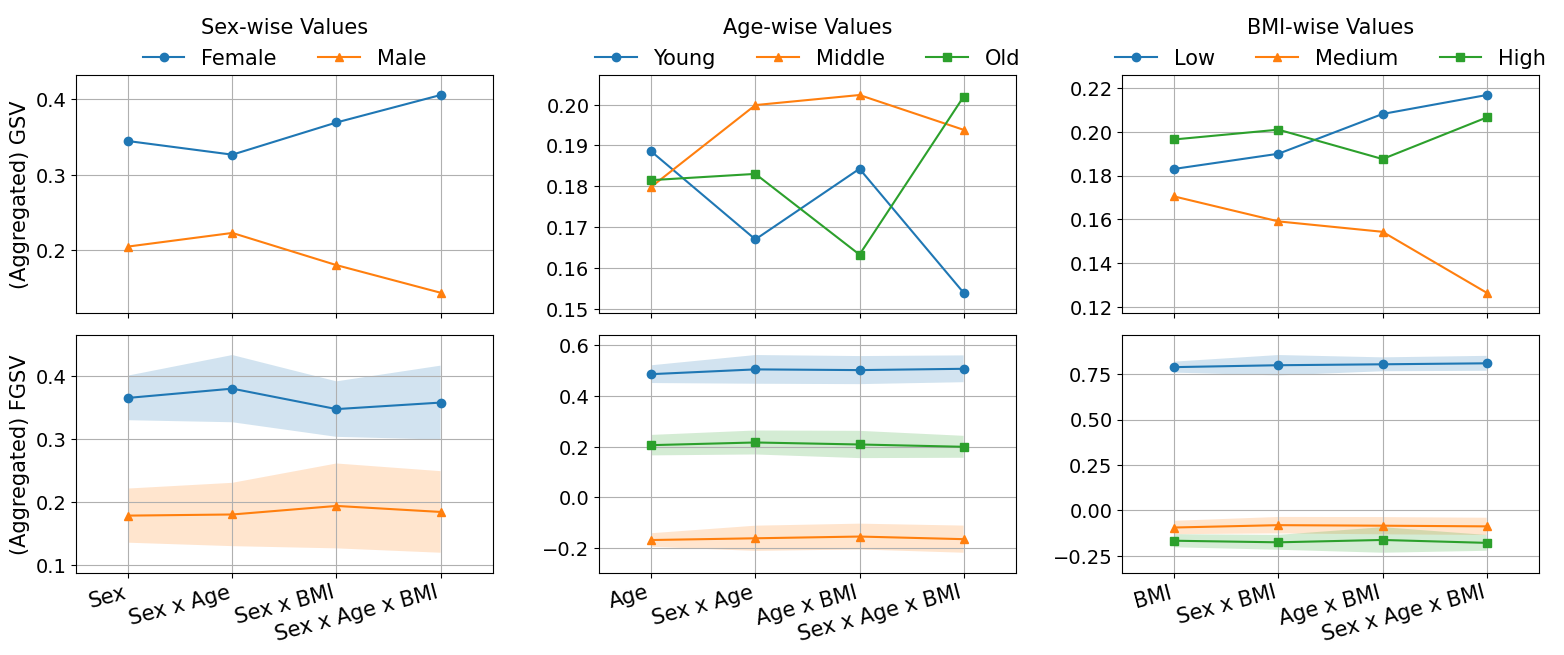
Figure 4: Comparison of GSV (top row) and FGSV (bottom row) in a regression task for explainable AI. Each column aggregates category-level values for a specific variable: sex (left), age (middle), and BMI (right).

Conclusion

The FGSV emerges as a more stable and reliable method for group data valuation, addressing inherent flaws in existing models that allow manipulation through subgroup partitioning. This solution not only enhances fairness in data-driven environments but also improves computational feasibility with a scalable algorithm. As the AI landscape continues to integrate ever-larger datasets, such a fair and efficient valuation framework will be indispensable for equitable data transactions and robust model interpretation.