Toward Portable GPU Performance: Julia Recursive Implementation of TRMM and TRSM (2504.13821v1)

Abstract: This paper presents a performant and portable recursive implementation of triangular matrix-matrix multiplication (TRMM) and triangular solve (TRSM) in Julia for GPUs, two kernels that underlie many linear-algebra algorithms. We restructure TRMM and TRSM so that most work is executed as general matrix-matrix multiplication (GEMM), improving use of the GPU memory hierarchy and reducing latency. Exploiting Julia's multiple dispatch and metaprogramming together with the GPUArrays and KernelAbstractions frameworks, we expose a single hardware-agnostic API that runs on NVIDIA, AMD, and Apple Silicon GPUs. For large matrices the recursive code reaches throughput comparable to vendor libraries such as cuBLAS and rocBLAS, while providing these routines on Apple Silicon for the first time. The entire implementation is only a few hundred lines of code, showing that unified Julia programs can deliver near-vendor performance across heterogeneous architectures.

• The paper presents a unified recursive framework for TRMM and TRSM, leveraging Julia's multiple dispatch and metaprogramming for hardware-agnostic performance.
• It decomposes triangular matrix operations into optimized GEMM calls to reduce memory accesses and boost concurrency on various GPU architectures.
• Benchmark results demonstrate that the recursive implementation achieves performance comparable to or surpassing vendor-optimized libraries like cuBLAS and rocBLAS.

Portable GPU Performance via Julia

This paper introduces a performant and portable implementation of TRMM and TRSM operations in Julia for GPUs, leveraging recursion and modern software abstractions. The implementation aims to address the challenges of achieving peak performance on GPUs compared to GEMM, which is often hindered by the triangular structure of input matrices and associated data dependencies. By using Julia's multiple-dispatch and metaprogramming features, the authors achieve hardware-agnostic execution across different GPU architectures, including Apple Silicon, with performance comparable to vendor-optimized libraries.

Background on TRMM and TRSM

The TRMM and TRSM algorithms are fundamental BLAS Level 3 routines used in various scientific and engineering applications. TRMM computes the product of a triangular matrix with another matrix, while TRSM solves triangular systems of linear equations. Existing GPU implementations, such as those in cuBLAS, often underperform compared to GEMM due to the challenges posed by the triangular structure, including WAR and RAW dependencies. To overcome these limitations, the paper adopts a recursive formulation that decomposes TRMM and TRSM into GEMM calls, which are highly optimized for GPU architectures. This restructuring reduces memory accesses, maximizes concurrency, and aligns better with GPU memory hierarchies.

Implementation Details

The implementation leverages Julia's {\tt GPUArrays.jl} and {\tt KernelAbstractions.jl} packages to achieve performance portability. {\tt GPUArrays.jl} allows users to generate GPU code for different hardware vendors by modifying the type signature of the input data. {\tt KernelAbstractions.jl} provides a kernel-level interface supported by different hardware backends, including {\tt CUDA.jl}, {\tt AMDGPU.jl}, {\tt oneAPI.jl}, and {\tt Metal.jl}. The recursive framework partitions input matrices into submatrices, with the triangular matrix $A$ divided into blocks $A_{11}$, $A_{21}$, and $A_{22}$, and the right-hand side matrix $B$ split into corresponding blocks $B_1$ and $B_2$ (Figure 1). The TRMM and TRSM algorithms then recursively solve smaller triangular systems and update the remaining blocks until the submatrices are small enough to handle directly.

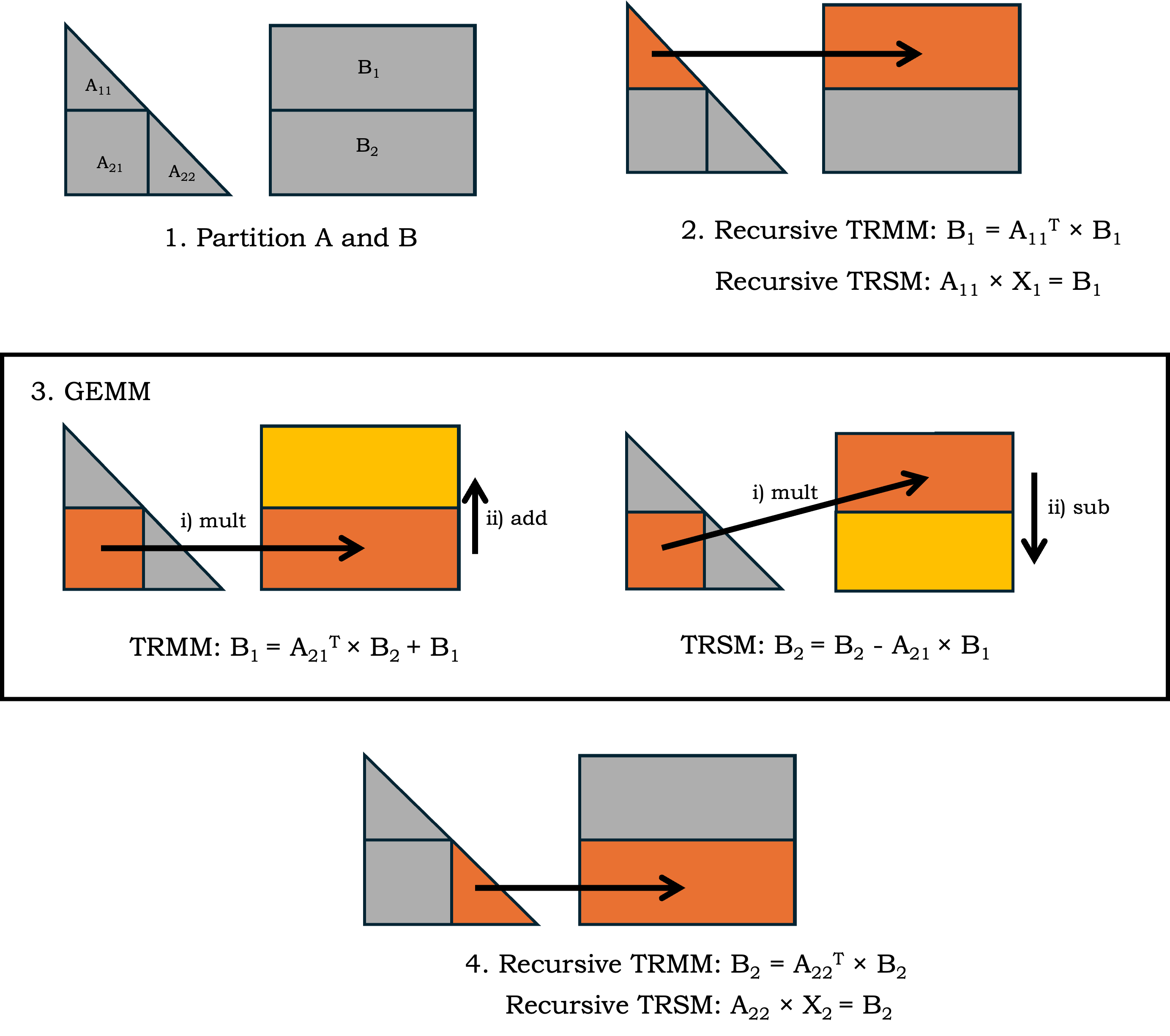
Figure 1: TRMM/TRSM Recursive Illustration.

The paper introduces a unified recursive framework that generalizes both TRMM and TRSM into a single recursive structure, using Julia’s multiple dispatch to dynamically determine the appropriate function at runtime. Kernel performance engineering techniques, such as memory optimization using shared memory and contiguous memory striding, are applied to optimize the base case GPU kernel performance. For the TRSM algorithm, the algorithm is reformulated to facilitate parallelism by distributing row computations across threads for each column, with synchronization occurring after each row.

Performance Evaluation

The performance of the unified implementation is benchmarked on different hardware platforms, including Apple, AMD, and NVIDIA GPUs. The results demonstrate that the implementation achieves runtime performance comparable to state-of-the-art cuBLAS/rocBLAS libraries. Figure 2 shows the runtime performance of TRMM and TRSM across the three different hardware platforms, demonstrating similar performance trends across hardware. The implementation provides the first implementation of recursive TRMM and TRSM functions for Apple Silicon GPUs.

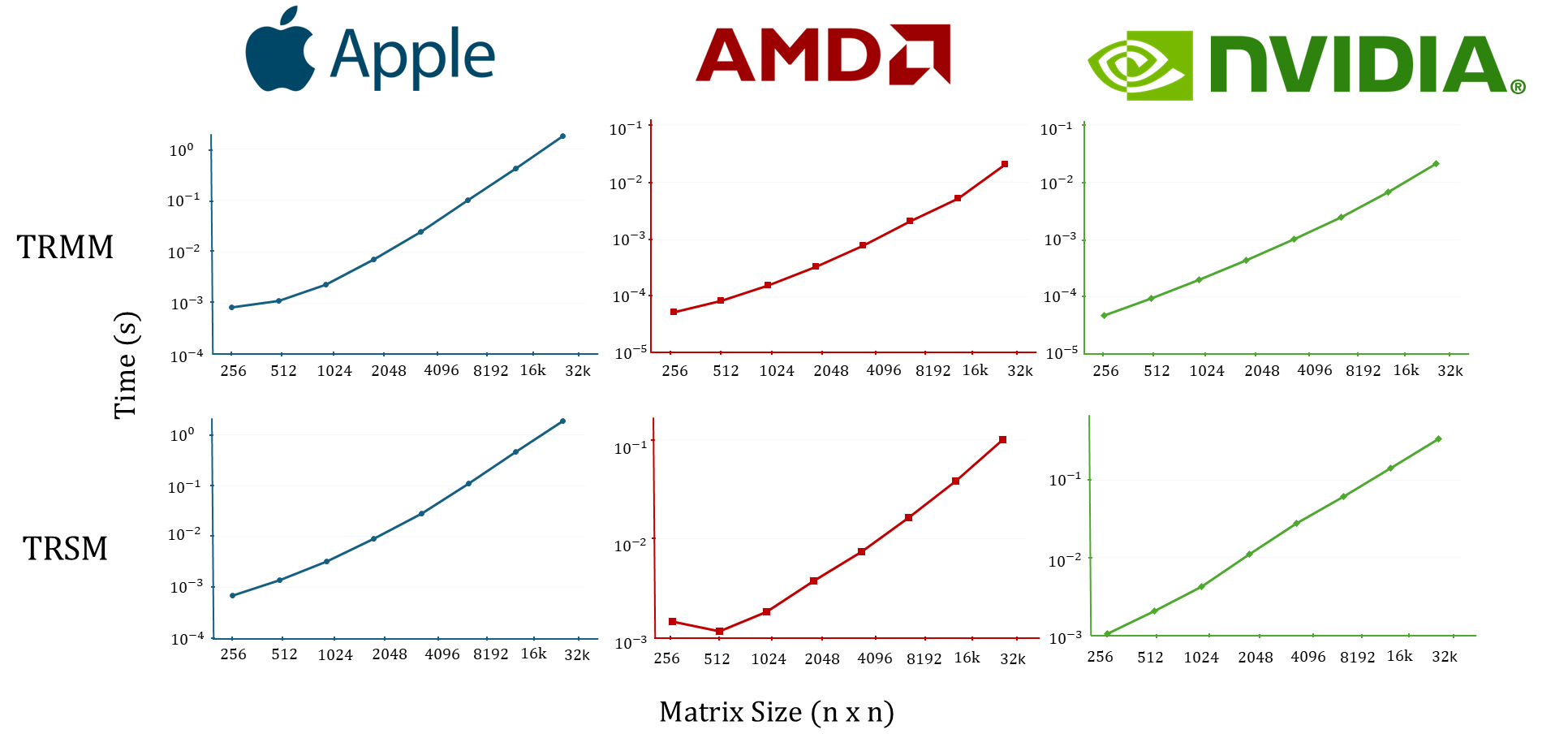
Figure 2: Runtime of recursive unified TRMM (top row) and TRSM (bottom row) functions across different GPU hardware platforms (Apple, AMD, NVIDIA) as a function of the size of the matrix (A \in \mathbb{R.

Figure 3 shows the ratio of runtime performance of cuBLAS/rocBLAS versus the Julia TRMM/TRSM implementations. The TRMM Julia implementation consistently outperforms both cuBLAS and rocBLAS for rectangular matrices. For square matrices, the TRMM Julia implementation performs similarly to or better than rocBLAS and similarly to cuBLAS. The TRSM Julia implementation matches or surpasses cuBLAS performance in most cases, with rocBLAS being faster for smaller matrices.

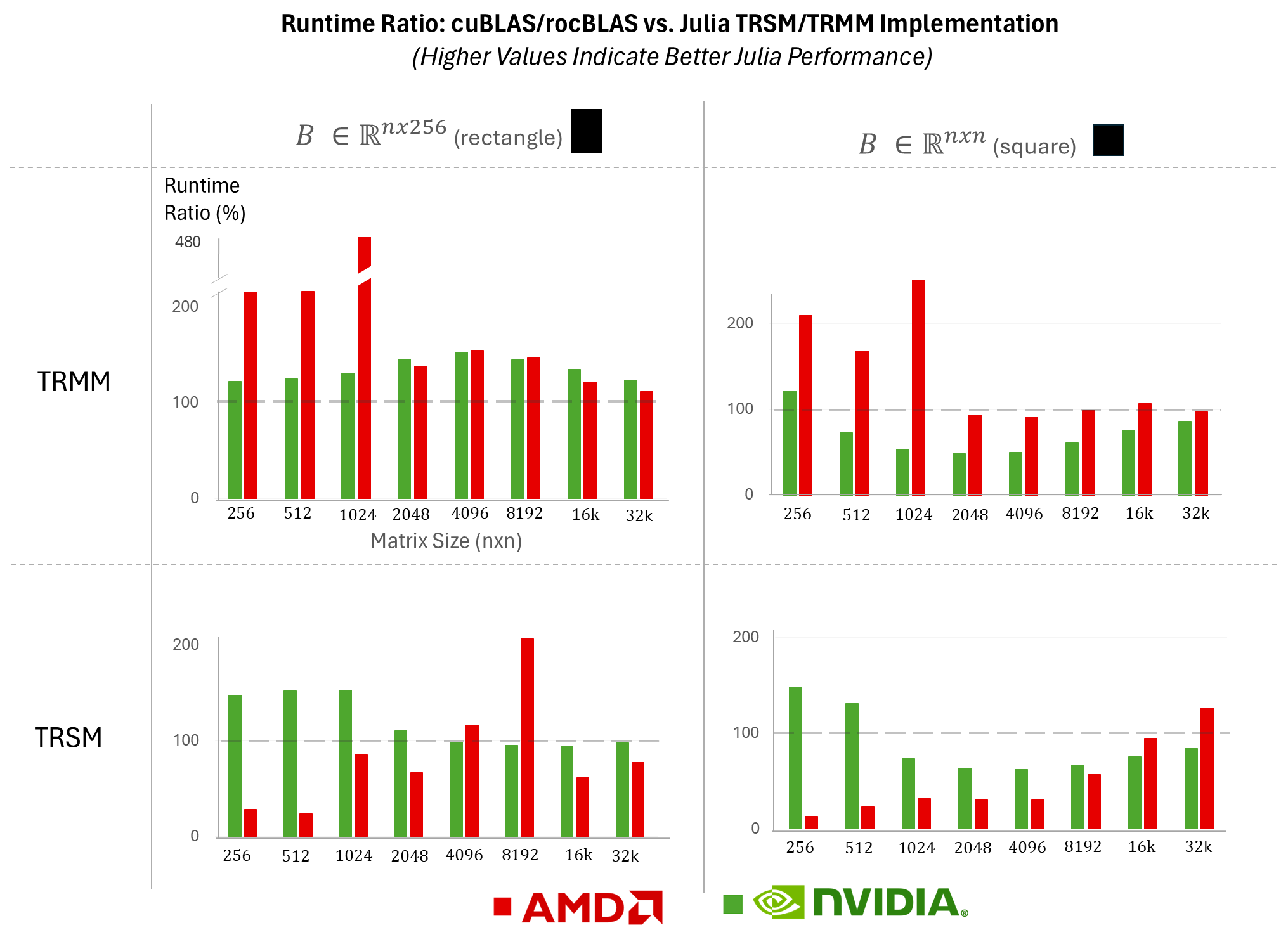
Figure 3: Runtime ratio of cuBLAS/rocBLAS versus the Julia implementation of TRMM (top row) and TRMM (bottom row) in function of the size of matrix (A \in \mathbb{R.

Conclusion

The paper presents a hardware-agnostic implementation of recursive TRMM and TRSM in Julia, achieving performance comparable to vendor-optimized libraries while providing portability across different GPU architectures. The implementation leverages Julia's multiple dispatch and metaprogramming capabilities, along with kernel performance engineering techniques, to optimize performance. The results demonstrate the feasibility of achieving performance portability with a relatively small amount of code. Future work involves advanced scheduling and extension to multi-core hardware settings using Dagger.jl [alomairydynamic] to optimize for the hardware without user effort.