DVHGNN: Multi-Scale Dilated Vision HGNN for Efficient Vision Recognition (2503.14867v1)

Abstract: Recently, Vision Graph Neural Network (ViG) has gained considerable attention in computer vision. Despite its groundbreaking innovation, Vision Graph Neural Network encounters key issues including the quadratic computational complexity caused by its K-Nearest Neighbor (KNN) graph construction and the limitation of pairwise relations of normal graphs. To address the aforementioned challenges, we propose a novel vision architecture, termed Dilated Vision HyperGraph Neural Network (DVHGNN), which is designed to leverage multi-scale hypergraph to efficiently capture high-order correlations among objects. Specifically, the proposed method tailors Clustering and Dilated HyperGraph Construction (DHGC) to adaptively capture multi-scale dependencies among the data samples. Furthermore, a dynamic hypergraph convolution mechanism is proposed to facilitate adaptive feature exchange and fusion at the hypergraph level. Extensive qualitative and quantitative evaluations of the benchmark image datasets demonstrate that the proposed DVHGNN significantly outperforms the state-of-the-art vision backbones. For instance, our DVHGNN-S achieves an impressive top-1 accuracy of 83.1% on ImageNet-1K, surpassing ViG-S by +1.0% and ViHGNN-S by +0.6%.

• The paper introduces DVHGNN, a multi-scale dilated vision HGNN that improves recognition by efficiently capturing high-order and multi-scale dependencies via dynamic hypergraph convolution.
• It employs innovative multi-scale hypergraph construction using cosine similarity clustering and dilated hypergraph construction to aggregate vertex features with sparsity-aware weights.
• Experimental results on ImageNet, MS-COCO, and ADE20K demonstrate superior accuracy and efficiency over baseline models like ViG and ViHGNN, validating the architecture's effectiveness.

DVHGNN: Multi-Scale Dilated Vision HGNN for Efficient Vision Recognition

The paper "DVHGNN: Multi-Scale Dilated Vision HGNN for Efficient Vision Recognition" (2503.14867) introduces a novel vision architecture, the Dilated Vision HyperGraph Neural Network (DVHGNN), designed to efficiently capture high-order correlations among objects by leveraging a multi-scale hypergraph representation. The method addresses the limitations of Vision Graph Neural Networks (ViGs) related to quadratic computational complexity from KNN graph construction and the constraint of pairwise relations in standard graphs.

Addressing Limitations of ViG and ViHGNN

ViG faces limitations in effectively representing complex inter-class and intra-class relationships due to its normal graph structure, which primarily models low-level, local connections. Furthermore, the KNN graph construction in ViG results in quadratic computational complexity and potential information loss due to its non-learnable nature. ViHGNN attempts to enhance ViG using hypergraphs but falls short due to limitations in hypergraph construction, which neglects local and multi-scale features, and reciprocal feedback, which constrains adaptability during learning. The DVHGNN architecture is shown in (Figure 1).

Figure 1: Architecture of the proposed DVHGNN. In each block, Multi-Scale(MS) DVHGNN block constructs multi-scale hyperedges, followed by message passing through vertex and hyperedge convolutions, and finalizes with ConvFFN to enhance feature transformation capacity and counteract over-smoothing.

Multi-Scale Hypergraph Construction

DVHGNN introduces a multi-scale hypergraph approach to image representation, using cosine similarity clustering and Dilated HyperGraph Construction (DHGC) techniques. This multi-scale hypergraph construction adaptively captures dependencies among data samples. The hypergraph is constructed using two distinctive hyperedge types: those derived from clustering and those obtained via DHGC, which are illustrated in (Figure 2).

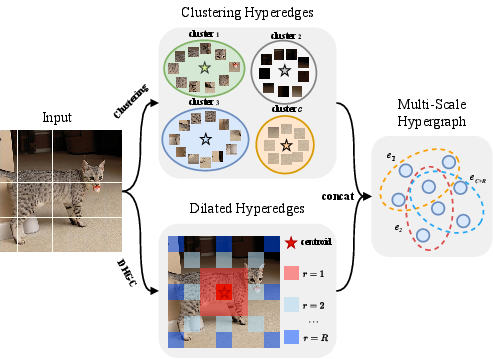
Figure 2: Illustration of Multi-Scale Hypergraph Construction (without region partition). The final hyperedge set is composed of two types of hyperedges: a set of size $C$ obtained from cosine similarity clustering, and a set of size $R$ derived from DHGC.

The clustering method groups vertices into distinct clusters based on their mutual similarities, mapping feature vectors into a similarity space and establishing centroids. The Dilated Hypergraph Construction (DHGC) enhances the hyperedge set by forming dilated hyperedges for each central vertex within a window, capturing multi-scale information with sparsity-aware weights. The final hypergraph is mathematically formulated to capture both local and extended neighbor information.

Dynamic Hypergraph Convolution (DHConv)

A dynamic hypergraph convolution mechanism facilitates adaptive feature exchange and fusion at the hypergraph level. DHConv consists of two stages: Vertex Convolution, which aggregates vertex embeddings to form hyperedge features, and Hyperedge Convolution, which distributes these features back to update the vertex embeddings. The two-stage message passing of the proposed Dynamic Hypergrpah Convolution (DHConv) is illustrated in (Figure 3).

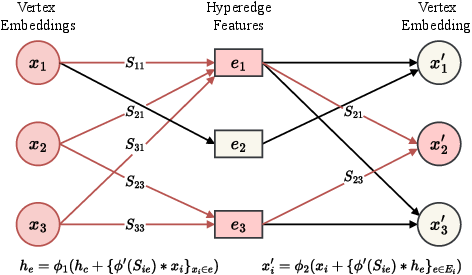
Figure 3: Illustration of two-stage message passing of our Dynamic Hypergrpah Convolution (DHConv). $h_{c}$ is the feature of the hyperedge centroid, $\mathbf{S}_{ie}$ is the cosine similarity matrix between vertices and hyperedge centroids, and $x_{i}$ and $x'_{i}$ represent the vertex feature before and after DHConv.

The Vertex Convolution leverages cosine similarity clustering hyperedges, adaptively aggregating features through dynamic learning. The feature aggregation process for clustering hyperedges involves cosine similarity between vertices and hyperedge centroids, while for dilated hyperedges, it captures multi-scale information efficiently using learnable, sparsity-aware weights. Hyperedge Convolution adaptively leverages hyperedge features to update vertex embeddings based on cosine similarity or hyperedge weights, inspired by the Graph Isomorphism Network (GIN).

Experimental Validation and Results

The authors conducted extensive experiments on benchmark image datasets to evaluate DVHGNN. On ImageNet-1K, DVHGNN-S achieved a top-1 accuracy of 83.1\%, outperforming ViG-S by 1.0% and ViHGNN-S by 0.6%. The comparison of FLOPs and Top-1 accuracy on ImageNet-1K is shown in (Figure 4).

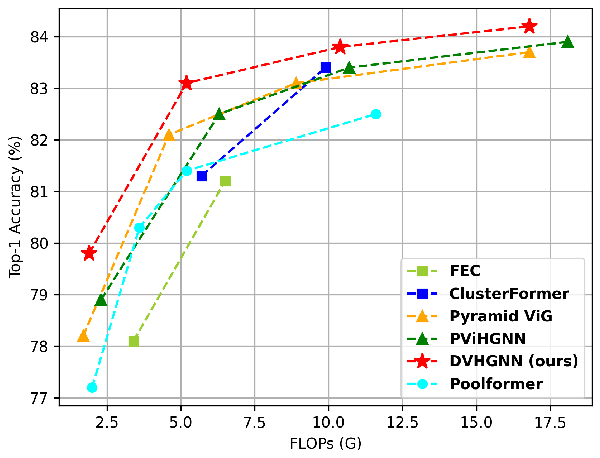
Figure 4: Comparison of FLOPs and Top-1 accuracy on ImageNet-1K. The proposed DVHGNN achieves the best performance compared to other state-of-the-art models.

Object detection and instance segmentation tasks on MS-COCO showed that DVHGNN-S achieved 43.3% mAP under the RetinaNet framework, surpassing ViG by 1.5% and ViHGNN by 1.1%. Under the Mask R-CNN framework, DVHGNN-S achieved 44.8% bbox mAP and 40.2% mask mAP, outperforming ViHGNN by 1.7% and 0.6%, respectively. Semantic segmentation experiments on ADE20K using Semantic FPN and UperNet frameworks also demonstrated superior performance compared to other backbones. Ablation studies validated the contributions of individual modules, with the visualization of the hypergraph structure shown in (Figure 5).

Figure 5: Visualization of the hypergraph structure of DVHGNN. The hypergraph structure is obtained by an overlay of hyperedges derived from the Clustering method and DHGC.

The visualization of cross-tasks clustering hyperedges in object detection and instance segmentation is shown in (Figure 6).

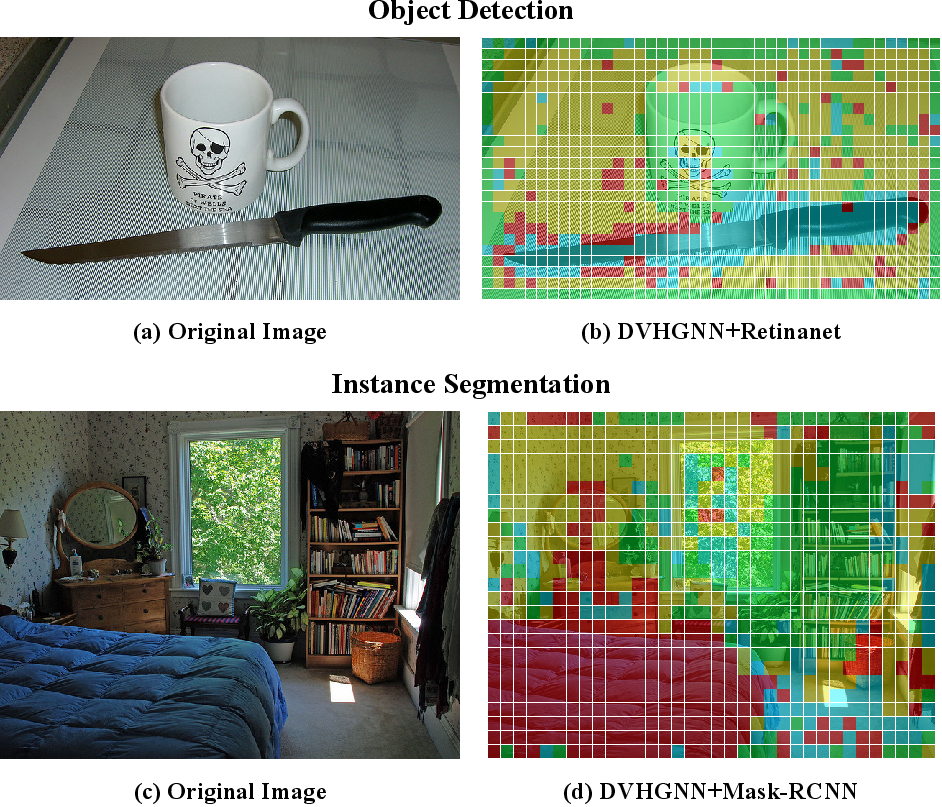
Figure 6: Visualization of cross-tasks clustering hyperedges in object detection and instance segmentation, respectively.

Conclusion

The paper presents DVHGNN, a novel vision backbone that learns hypergraph-aware vision features through a dynamic, learnable hypergraph. The method adaptively captures multi-scale dependencies and aggregates vertex features into hyperedge features using a novel dynamic hypergraph convolution. The qualitative and quantitative results demonstrate the effectiveness of DVHGNN in enhancing the learning performance of various vision tasks. Future work will explore the scalability and generalization of DVHGNN across additional vision tasks.