A Tutorial on Knots and Quantum Mechanics (2503.08846v2)

Abstract: These notes review a description of quantum mechanics in terms of the topology of spaces, basing on the axioms of Topological Quantum Field Theory and path integral formalism. In this description quantum states and operators are encoded by the topology of spaces that are used as modules to build the quantum mechanical model, while expectation values and probabilities are given by topological invariants of spaces, knots and links. The notes focus on the specific way the topology encodes quantum mechanical features, or, equivalently, on how these features can be controlled through the topology. A topological classification of entanglement is discussed, as well as properties of entanglement entropy and basic quantum protocols. The primary aim is to build a less conventional diagrammatic intuition about quantum mechanics, expanding the paradigm of ``Quantum Picturalism".

• The paper demonstrates that quantum states and operators can be systematically mapped to knots and diagrams, providing a robust topological framework for quantum mechanics.
• It employs skein relations and the Temperley–Lieb algebra to compute knot invariants, bridging algebraic techniques with diagrammatic representations.
• The study outlines practical applications in quantum algorithms and entanglement analysis, offering valuable insights for topological quantum computation.

Knots, Topology, and Quantum Mechanics: A Diagrammatic Framework

The paper "A Tutorial on Knots and Quantum Mechanics" (2503.08846) systematically develops an approach to quantum mechanics based on topological and diagrammatic methods, especially via the formalism of Topological Quantum Field Theory (TQFT) and its connections to knot theory. The work leverages the categorical, functorial properties underlying quantum theory and exhibits a systematic mapping between (multi)linear algebraic objects—states, operators, Hilbert spaces—and manifolds and knots in low dimensions. This diagrammatic "quantum picturalism" is both technically rigorous and provides valuable intuition for quantum information, entanglement, and even quantum algorithms.

---

From Knot Theory to Topological Quantum Field Theory

The opening sections introduce the key combinatorial and algebraic structures of knot theory, focusing particularly on the bracket version of the Jones polynomial and its efficient calculation using skein relations.

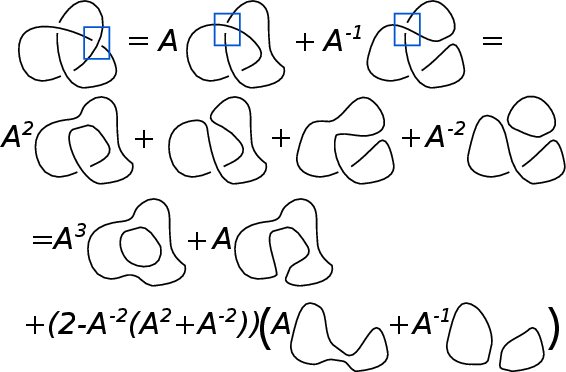
Figure 1: Calculation of the bracket polynomial of the trefoil knot $3_1$ using skein relations.

Knot invariants—classical (linking number) and quantum (Jones polynomial, HOMFLY-PT)—are efficiently computable by iterative application of local diagrammatic relations (skein relations and Temperley-Lieb algebraic generators). The paper demonstrates, through explicit matrix constructions, how these diagrammatic relations can be directly mapped to matrix traces or overlap formulas for quantum states, formalizing the close relationship between link invariants and partition functions/path integrals in certain quantum field theories.

---

Category Theory and the Axiomatic Structure of Quantum Mechanics

A central pillar of the exposition is Michael Atiyah's axiomatization of TQFTs as functors from the category of cobordisms to the category of vector spaces—objects are manifolds (state spaces), and morphisms are cobordisms (evolution, operators).

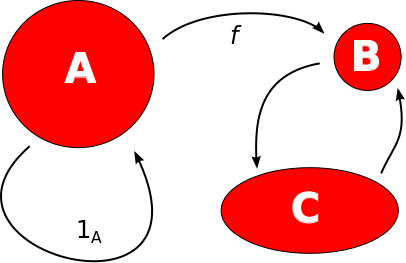
Figure 2: A schematic depiction of a category (objects and morphisms).

This formulation provides a precise technical backing for representing quantum states and operators as topological spaces (with boundaries and glueings for compositions). In this framework, the inner product, trace, and tensor product operations all acquire geometric/topological analogues—typically as specific gluings or closures of manifolds.

---

Diagrammatic Quantum Mechanics: Topobits and the Skein Module

The development then specializes to 1D and 3D models—"topological quantum mechanics" realized either via simple diagrams (strands, crossings) or by construction as states in Chern-Simons theory. The use of the Temperley-Lieb/Jones-Wenzl diagrammatic language allows for an explicit, calculable basis for Hilbert spaces, with basis vectors corresponding to noncrossing pairings ("connectome classes"), and operators as compositions of braids and projectors.

Explicitly:

• Basis states are noncrossing diagrams of $2n$ points (dimension is Catalan number $C_n$ in the generic case).
• Any state is a linear combination of such diagrams, with scalar products computed via the same rules as bracket polynomials.
• Actions of braid group elements (as unitary gates) and projections (Temperley–Lieb projectors) generate all physically relevant manipulations.

This provides, in practice, a direct route to representing quantum operations (and protocols) as sequences of local diagrammatic transformations, closely paralleling tensor network and quantum circuit models.

---

Entanglement, SLOCC Classifications, and Entanglement Entropy

A substantial part of the tutorial is devoted to how quantum entanglement and its structure emerge from connectivities in the diagrammatic TQFT model:

• Separable states correspond to diagrams where subsystems are unlinked (disconnected).
• Bipartite and multipartite entangled states correspond to diagrams with lines (and more general tangles) connecting boundaries.
• SLOCC classification is realized via the equivalence classes under invertible local operator actions; the number of connecting strands (between subsystems) corresponds to the Schmidt rank of the state.

The von Neumann (entanglement) entropy acquires a direct diagrammatic/topological definition:

• For large-$k$ (semiclassical, connectome) limits, the entropy is given by log of the number of connections (effectively counting minimal cuts—directly paralleling the Ryu–Takayanagi formula in holography).

Thus, diagrammatic calculus not only gives a robust technical generalization of entanglement structure but also efficiently encodes the computation of entropy and mutual information inequalities (subadditivity, strong subadditivity).

---

Quantum Algorithms in Topological Models

The framework is shown to be directly applicable in representing and analyzing basic quantum algorithms:

• Quantum teleportation is described diagrammatically: measurement in the Bell basis corresponds to projecting onto specific diagrams; correction is implemented as (un)twisting via braid group elements.
• Dense coding is similarly encoded as local (or nonlocal) operator insertions, with explicit mappings between classical bit values and braid group elements.

The model exposes the essential role of maximally entangled states (Bell states) as distinguished diagrams, the necessity of using appropriate measurement (projector) bases, and the consequences of non-orthogonal diagrammatic bases (Temperley-Lieb algebra's intrinsic nonorthogonality).

---

Nonunitarity and Topological Defects

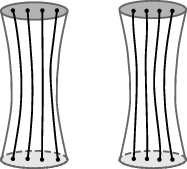
Figure 3: Topological operators acting on tensor products of two Hilbert spaces are in general nonunitary. Contracting an operator with its unitary conjugate creates a topological defect, preventing the result to be an identity matrix.

The framework carefully points out that topological operators (tangles, braids, projectors) applied on tensor product Hilbert spaces may not always be unitary—such constructions can introduce topological defects (holes or handlebodies), manifest in the failure of operator $\hat O^\dagger \hat O$ to produce the identity. This is a critical observation for practitioners who wish to realize topological gate sets in experiments or quantum simulation: ensuring unitarity at the diagrammatic level requires careful restricted choices (e.g., to braidings or local projectors).

---

Extensions and Open Problems

Several important directions for further development and application are delineated:

• Orthogonal diagrammatic bases: While Temperley-Lieb provides a convenient combinatorial basis, it is not orthogonal, complicating certain quantum information tasks—alternatives using conformal blocks/generalized Jones–Wenzl projectors can resolve this but often obscure intuitive topological manipulations.
• Multipartite entanglement: Bipartite connectome diagrams correspond closely with SLOCC classes and Schmidt ranks, but for multipartite systems (e.g., GHZ vs. W), the connectome limit provides only a partial classification—additional topological data or combinations may be required.
• Limiting behavior and quantum gravity: The identification of minimal cuts/surfaces in diagrammatic calculus with entanglement entropy mirrors the Ryu–Takayanagi formula and supports emergent spacetime/geometry paradigms in quantum gravity.
• Implementation and simulation: The explicit mapping to braid group representations suggests practical routes to topological quantum computation with anyonic systems—diagrammatic/topological models provide not only theoretical insight but also an effective algorithmic toolbox for simulation, code analysis, and protocol verification.

---

Conclusion

This work presents a comprehensive categorical and diagrammatic formalization of quantum mechanics, with explicit algebraic and topological tools grounded in the machinery of TQFT, knot theory, and category theory. The translation of quantum states, entanglement, operators, and protocols into manipulations of topological diagrams provides not only a rigorous mathematical language but also a valuable computational and pedagogical paradigm. The trade-offs between basis choice, computational efficiency, and the range of physical phenomena captured are clearly articulated, making this exposition directly useful for applications in quantum computation, quantum information, and the paper of quantum gravity and holography. This diagrammatic formalism is poised for further development, especially in the context of multipartite entanglement, error-correcting codes, and experiments with topological phases of matter.