Thermal Macroeconomics: An axiomatic theory of aggregate economic phenomena (2412.00886v3)
Abstract: An axiomatic approach to macroeconomics based on the mathematical structure of thermodynamics is presented. It deduces relations between aggregate properties of an economy, concerning quantities and flows of goods and money, prices and the value of money, without any recourse to microeconomic foundations about the preferences and actions of individual economic agents. The approach has three important payoffs. 1) it provides a new and solid foundation for aspects of standard macroeconomic theory such as the existence of market prices, the value of money, the meaning of inflation, the symmetry and negative-definiteness of the macro-Slutsky matrix, and the Le Chatelier-Samuelson principle, without relying on implausibly strong rationality assumptions over individual microeconomic agents. 2) the approach generates new results, including implications for money flow and trade when two or more economies are put in contact, in terms of new concepts such as economic entropy, economic temperature, goods' values and money capacity. Some of these are related to standard economic concepts (eg marginal utility of money, market prices). Yet our approach derives them at a purely macroeconomic level and gives them a meaning independent of usual restrictions. Others of the concepts, such as economic entropy and temperature, have no direct counterparts in standard economics, but they have important economic interpretations and implications, as aggregate utility and the inverse marginal aggregate utility of money, respectively. 3) this analysis promises to open up new frontiers in macroeconomics by building a bridge to ideas from non-equilibrium thermodynamics. More broadly, we hope that the economic analogue of entropy (governing the possible transitions between states of economic systems) may prove to be as fruitful for the social sciences as entropy has been in the natural sciences.
Summary
- The paper introduces Thermal Macroeconomics, demonstrating how axioms modeled on thermodynamics can underpin aggregate economic phenomena.
- It outlines novel metrics such as economic entropy and temperature, providing measurable analogues for inflation and trade dynamics.
- The framework leverages a Carnot cycle analogy to illustrate non-decreasing aggregate utility from trade and improved monetary flow efficiency.
Thermal Macroeconomics: An Axiomatic Theory of Aggregate Economic Phenomena
Thermal Macroeconomics proposes an innovative framework that parallels classical thermodynamics to offer insights into macroeconomic theory. The approach deduces fundamental relations among aggregate properties—such as money flow, trade, and the value of money—without relying on conventional microeconomic foundations.
Axiomatic Framework
The theory introduces the concept of Thermal Macroeconomics (TM) by adopting axioms akin to those in thermodynamics. These axioms underpin an approach that provides a more robust foundation for understanding macroeconomic phenomena, such as market prices and inflation, than models that assume rational behavior of individual agents. The axioms focus on scalability and extensivity assumptions, drawing parallels with thermodynamic concepts like energy and entropy.
Economic Entropy and Temperature
TM introduces novel concepts of economic entropy and economic temperature. Economic entropy is depicted as an aggregate utility that systems strive to maximize, mirroring the second law of thermodynamics whereby entropy in a closed system tends not to decrease. Entropy is grounded in economic realities as an aggregate measure of states, independent of individual agent preferences. Economic temperature is similarly defined, pinpointing the inverse marginal utility of money.
Figure 1: An economic Carnot cycle in the plane of amount of goods and temperature for an island economy with , , operating between two mainland economies at temperatures and $T_C=0.24.
Trade and Market Dynamics
The model presents innovative ways to analyze trade dynamics without detailed micro-level interactions. Trade, when allowed between economies, always results in non-decreasing aggregate utility, introducing a measure for the potential gains from trade. This framework notably incorporates the analogy of a Carnot cycle, enabling the extraction of monetary gains from differences in economic temperatures akin to extracting work from temperature differences in physics.
Practical Implications and Measurement Techniques
The concept of economic temperature provides a fresh understanding of inflation, characterized as the rate of increase in economic temperature. TM proposes using ship thermometers for practical measurement of this temperature, thereby facilitating comparative economic analysis without reliance on fixed baskets of goods.
Figure 2: An Edgeworth box plot for the two Cobb-Douglas economies, illustrating mutual benefits from trade increasing the entropy of each economy.
Cross-Disciplinary Extensions
Insights from thermodynamics are extended to explore and quantify phenomena such as production, consumption, and labor, transcending the limits of exchange economies. TM anticipates addressing the intricacies of currency systems, labor markets, and real-world complexities of economic systems by leveraging fundamental thermodynamic principles.
Figure 3: Relationship between volume (quantity of goods) and price, with changes at a constant temperature (light lines) and entropy (heavy lines). The equal area rule clarifies the trading implications within the PV and TS coordinates.
Conclusion
The thermal macroeconomic model stands to revolutionize macroeconomic analysis by offering an axiomatic foundation to describe aggregate economic behavior. By integrating principles from thermodynamics, TM holds potential for wide-ranging applications in economic policy, trade negotiations, and inflation control, promising a shift towards more empirically grounded economic science. The framework invites further exploration of extensions to non-equilibrium systems, opening discussions for incorporating dynamic socio-economic factors.
Incorporating the deep insights of thermodynamics into economics may yield a profound understanding of economic systems as holistic entities, with laws governing aggregate behaviors offering predictive power and insight into economic dynamics.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a consolidated list of specific gaps and unresolved questions that emerge from the paper and suggest concrete directions for future research.
- Empirical measurement: How can economic entropy and temperature be operationalized and consistently measured in real economies from observable data (prices, quantities, monetary aggregates), including confidence intervals and robustness to data revisions?
- Thermometer design: What concrete protocols, instruments, and data inputs are required to implement the proposed “economic thermometer” for temperature, and how can measurement error and market frictions be accounted for?
- Validation of the second law: Do real-world money flows between economies (countries, regions, sectors) statistically align with predicted entropy-increasing directions and temperature equalization? Design tests using cross-border payments, remittances, and capital flow datasets.
- Timescales to equilibrium: What determines the speed of temperature equalization and entropy change in financially joined economies, and how do transaction costs, capital controls, and network topology slow or prevent equilibration?
- Scope of A0 (unique statistical equilibrium): What micro-level behavioral and market interaction conditions guarantee uniqueness (ergodicity/mixing), and how robust is A0 to herding, coordination failures, or institutional constraints?
- Multiple equilibria and decomposability: How should the framework be extended to systems with persistent segmentation (barriers, islands, submarkets) and multiple stable equilibria; what additional state labels or order structure are needed?
- Path dependence of financial joins: Under what necessary and sufficient conditions is the equilibrium of a financial join independent of how the join is implemented (sequence, channels, frictions), and how large are deviations when independence fails?
- Non-equilibrium TM: How should non-equilibrium thermodynamics concepts (entropy production, flux–force relations) be translated to economics to model cycles, crises, and persistent disequilibria; what are the right macro “currents” and “forces”?
- Production and consumption: How can the axioms and state variables be generalized beyond pure exchange to include production, depreciation, consumption, capital accumulation, inventories, and time-to-build constraints?
- Finance and credit: How to incorporate endogenous money creation, bank balance sheets, credit constraints, leverage, default, and interest rates while maintaining a coherent notion of “conservation of money” and accessible states?
- Multi-currency systems: How to extend the theory to multiple monies with exchange rates, currency substitution, arbitrage, and capital controls; what replaces a single money coordinate and how is “temperature” defined across currencies?
- Pure vs commodity money: How do results change when money has intrinsic utility or storage cost; what are testable implications of the “pure money” construct and how to detect it empirically?
- Goods heterogeneity and indivisibilities: How to relax assumptions of divisibility and indistinguishability to include discrete goods, quality differences, perishability, and non-durables; how does this affect entropy existence and concavity?
- Extensivity and non-extensive systems: Many economies exhibit increasing returns, network effects, and “lumpiness.” What is the appropriate generalization of entropy and temperature in non-extensive settings, and which axioms must be modified?
- Accessibility with realistic constraints: The external trader is assumed to have unlimited goods and money and zero transaction costs. How to model accessibility when the trader is finite, faces constraints, and markets have frictions and legal barriers?
- Concavity/differentiability of entropy: Precisely characterize the conditions under which economic entropy is concave, differentiable, and additive; identify cases where concavity fails (e.g., strong complementarities, externalities) and the implications for stability.
- Uniqueness/normalization of entropy: To what extent is the entropy function unique (up to affine transformations) under the economic axioms, and how should normalization be chosen for empirical comparability across economies?
- Prices and “values”: The paper proposes macro “values” of goods and links to prices and reversible trade. What are necessary and sufficient conditions for market prices to coincide with these values, and how large can deviations be under frictions or market power?
- Cross-derivative relations: Can the predicted symmetry/negative-definiteness (macro Slutsky-like properties) and “flexibilities” be estimated from data, and do they hold across sectors and time? Develop econometric identification strategies.
- Money capacity: How can “money capacity” be defined, measured, and linked to observable aggregates (e.g., money velocity, liquidity ratios)? What determines it structurally, and how do policy levers affect it?
- Reversible trade in practice: With transaction costs and taxes, how close can real trades approach reversibility? Derive bounds on entropy changes under typical frictions and provide empirical tests.
- DSGE and TM integration: What is the mapping between TM’s entropy/temperature and DSGE primitives (preferences, technologies, shocks)? Can TM provide constraints that improve DSGE identification or calibration?
- Welfare interpretation: If entropy is “aggregate utility,” what is its relationship to welfare under heterogeneity and inequality? When (if ever) does entropy increase coincide with Pareto improvements or social welfare gains?
- Inequality and distribution: How do agent-level distributions (wealth, income, preferences) shape macro entropy and temperature; what are the distributional consequences of entropy-increasing transitions?
- Crises and large deviations: How do entropy and temperature behave near abrupt transitions (sudden stops, liquidity crises)? Can TM provide early-warning indicators or bounds on crisis probabilities?
- Calibration and simulations: Beyond the cited simulations, what broader classes of micro models (heterogeneous agents, networked trading, behavioral rules) reproduce TM predictions, and where do they fail?
- Identification from limited data: With incomplete information on quantities and microstates, what minimal datasets are sufficient to identify entropy gradients and temperature differences?
- Policy design: How can fiscal/monetary policies (taxes, subsidies, QE, capital controls) be framed as entropy/temperature interventions, and what constraints does the “second law” impose on feasible policy transitions?
- Exchange rates and inflation: The paper proposes a currency value independent of baskets. How does this relate to CPI-based inflation and purchasing power parity, and can inconsistencies be quantified and exploited for prediction?
- Network structure of contacts: How do money and goods-flow network structures affect equilibria, entropy production, and propagation of shocks; what are the analogues of transport coefficients in networked economies?
- Cyclic money flows: The transitivity of financial equilibrium rules out net cycles in equilibrium. Yet carry trades and global imbalances suggest persistent cycles. Under what conditions does the axiom fail, and how should TM be adapted?
- Robustness to changing technology and preferences: The theory assumes stationary statistical equilibria. How can slow structural change (technology adoption, preference drift) be incorporated as quasi-static processes with trackable entropy?
- Testing the Carnot-like cycle: What empirical settings would allow observation or implementation of a Carnot-analogue trading strategy; what are the expected returns net of frictions, and how to isolate temperature-ratio effects from price differentials?
- State-space completeness: What additional state variables (institutions, legal constraints, collateral quality) may be required to ensure that the macro state fully captures constraints on accessibility?
- Micro-to-macro mapping beyond Cobb–Douglas: How do different micro utility forms (CES with low/high elasticity, Leontief, habit formation) aggregate into macro entropy; derive general aggregation theorems and counterexamples.
- Relation to arbitrage conditions: How does no-arbitrage in asset markets interact with temperature equalization and entropy constraints; can TM generate new asset pricing restrictions testable in financial data?
- Treatment of services and intangibles: How should non-storable services and intangible capital be included in the state variables and accessibility framework, and what is their impact on measured temperature?
Conceptual Simplification
Big picture
The paper proposes “Thermal Macroeconomics” (TM): a way to explain large-scale economic behavior using the same mathematical structure that makes thermodynamics so powerful in physics. The goal is to derive reliable relationships between aggregate quantities (money, goods, prices, trade flows) without assuming anything specific about individual people’s preferences or decisions. Instead, the theory starts from a few high-level assumptions about how whole economies behave when they are allowed to interact.
Key ideas in plain language
Think of money like energy in physics: it can move between parts of an economy and is conserved at the macro level (aside from identifiable injections or removals, like printing money or taxes). The paper shows that, under mild assumptions, there exists:
- An “economic entropy” S that captures aggregate well-being or “aggregate utility” of an economy in a cardinal way (not just up to relabeling).
- An “economic temperature” T that measures how valuable an extra unit of money is, at the macro level. More precisely, the inverse temperature is the marginal aggregate utility of money:
With these definitions, the authors establish an economic version of the second law:
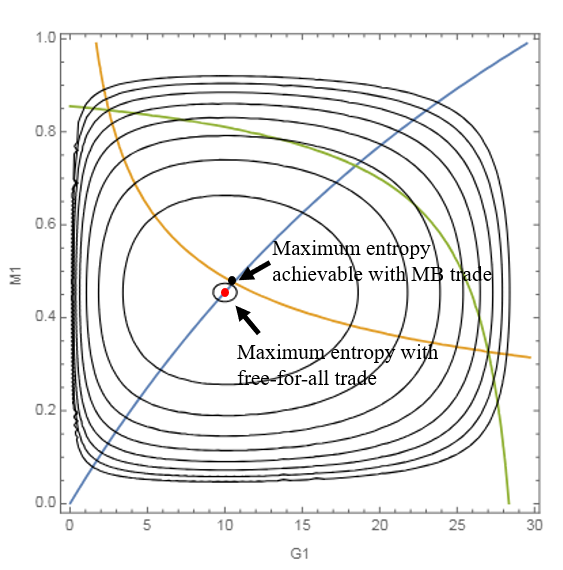
- When economies (or parts of an economy) are allowed to interact freely, the total entropy cannot decrease: ΔS ≥ 0.
This single principle explains which aggregate changes are possible and which are not. It also implies simple rules of thumb:
- Money tends to flow from higher-temperature economies to lower-temperature ones until their temperatures equalize (financial equilibrium).
- Trade flows (in goods or money) are “allowed” only if they increase total entropy.
What the paper delivers
To make the contributions easy to scan, here is a concise list of what the paper claims and why it matters.
- A macro-level foundation for prices and the value of money
- TM derives the existence of prices and the value of nominal currency without appealing to individual rationality or arbitrary “baskets of goods.” Prices arise via “values” assigned to goods in equilibrium, inferred from entropy and temperature.
- Economic entropy and temperature as operational, measurable quantities
- Entropy S is “aggregate utility” of the whole economy; temperature T summarizes how valuable another unit of money is. The paper proposes how to measure T (an “economic thermometer”) and explores “money capacity,” the analogue of heat capacity, describing how an economy’s temperature changes as money is added or removed.
- A macro second law with testable implications for trade and capital flows
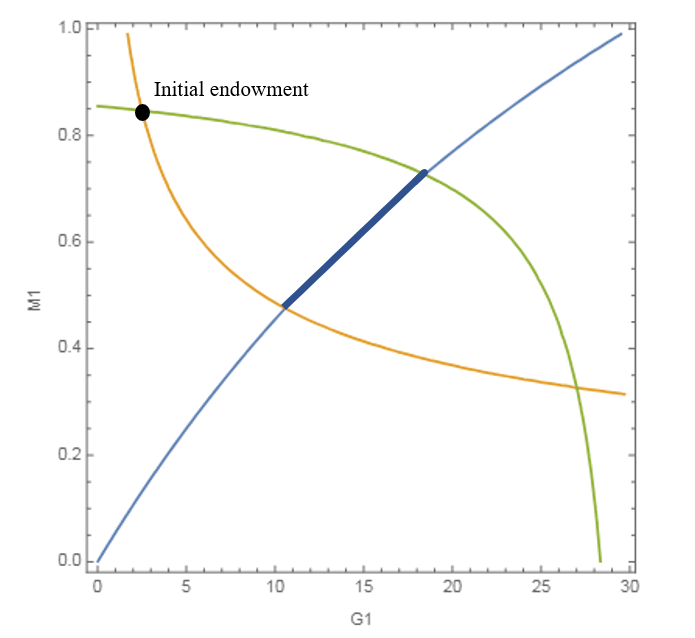
- When two economies are put in financial contact, net flows occur if and only if they raise total entropy. A special subset of trades raises the entropy of each economy individually—these are the “mutually beneficial” trades. This gives a crisp, quantitative criterion for when trade should happen and in which direction.
- A clean explanation for financial equilibrium and arbitrage-like strategies
- Financial equilibrium occurs when temperatures match, so there is no net flow of money. The paper illustrates “engines” that profit from temperature differences (an economic analogue of the Carnot cycle), and also how to make money from price differences across economies in a way consistent with the second law.
- Macro counterparts of standard micro results, but without micro assumptions
- TM recovers well-known properties—such as symmetry and negative definiteness of a macro Slutsky matrix and the Le Chatelier–Samuelson principle—purely from the entropy framework. It also produces Maxwell-like cross-derivative relations (here called “flexibilities,” the inverse of standard elasticities).
- Axiomatic clarity and extensibility beyond equilibrium
- The theory adapts Lieb and Yngvason’s axioms from thermodynamics to economics (e.g., “accessibility” of states, “financial joins,” and statistical equilibrium), proving the existence and concavity of S, and then defining T. Because the framework is thermodynamic, it naturally points toward extensions to non-equilibrium macroeconomics (persistent flows, cycles), where many real-world phenomena live.
- New conceptual tools (and how they relate to familiar ideas)
- “Economic entropy”: aggregate, cardinal utility of the whole economy.
- “Temperature”: inverse marginal aggregate utility of money; equalizing temperatures is the condition for financial equilibrium.
- “Money capacity”: how sensitive T is to money injections.
- “Values” of goods: macro constructs that produce market prices.
- “Pure money”: an idealized currency with no intrinsic consumption value, useful for clarifying the role of money as a numeraire.
How the theory is built
The authors restrict attention to “exchange economies” (no production or consumption—just redistribution of existing goods and money) and assume “extensivity” (larger systems are built from similar smaller parts). They posit a mild equilibrium assumption: for fixed amounts of goods and money, the economy settles into a unique statistical equilibrium (a steady probability distribution over micro-configurations). Using axioms adapted from thermodynamics, they:
- Define when one macro-state is reachable from another (accessibility) under allowed external interventions (e.g., a trader with unlimited inventory who must end with the same non-money assets).
- Prove the existence of an entropy function S consistent with these accessibility relations, and a second law: in any spontaneous or allowable transformation, total S cannot fall.
- Define temperature T from how S changes with money, and show that equal T characterizes financial equilibrium between economies in contact.
- Use these ingredients to derive prices, cross-derivative relations, and trade conditions.
Intuition via simple examples
- Financial contact: Let two economies exchange only money (no goods). If one has higher temperature (money is “worth less at the margin”), money tends to flow out until temperatures match. This is the macro version of “equalizing marginal utilities,” but no agent-level optimization is assumed.
- Carnot-like trading: A trader can profit by moving money and goods around a cycle that exploits persistent temperature differences, just as a heat engine draws work from a temperature gradient. The maximum profit rate depends only on those temperature differences.
Relationship to standard economics
TM recovers—and reframes—familiar results:
- Prices emerge as dual variables defined by the entropy structure, not by solving utility maximization at the agent level.
- Slutsky symmetry, negative definiteness, and the Le Chatelier–Samuelson principle appear as consequences of concavity and cross-derivative identities of S (analogous to Maxwell relations).
- The value of money is pinned down by macro laws, not by arbitrary baskets.
At the same time, TM brings genuinely new constructs (entropy, temperature, money capacity) and a second-law perspective that yields crisp, global constraints on what aggregate changes are feasible.
Scope and limitations
The current paper focuses on:
- Exchange economies (no production or consumption yet).
- A single currency (“money” as the numeraire).
- Extensive systems with a unique statistical equilibrium.
- Financial contact as the main interaction channel.
The authors discuss how to relax these constraints (multiple currencies, production, credit, persistent out-of-equilibrium flows) and report that simulations and a Cobb–Douglas example are consistent with the TM predictions. The broader promise is a pathway to non-equilibrium macroeconomics that retains analytical discipline while speaking directly to aggregate data.
One-line takeaway
By importing the axiomatic core of thermodynamics, the paper constructs a macro-level entropy and temperature for economies and uses them to derive prices, the value of money, and the direction of trade—yielding both familiar economic regularities and new, testable predictions, all without micro-level rationality assumptions.
Evaluation & Metrics Analysis
Overall assessment
The paper is primarily a theory-building contribution. Its “evaluation methodology” is therefore internal: the authors (i) adopt an axiomatic framework adapted from Lieb–Yngvason’s thermodynamics, (ii) derive existence, concavity, and comparative‑statics properties for macroeconomic analogues of entropy, temperature, and prices, and (iii) sanity‑check the framework via a worked “toy” example (Cobb–Douglas exchange economy) and by mapping to selected familiar economic results (e.g., macro Slutsky symmetry, Le Chatelier–Samuelson principle). They also point to a companion simulation paper (LMC) for micro‑founded validation, and sketch how one might measure “temperature” (a “thermometer” economy).
For a foundational axiomatic paper, this internal evaluation is appropriate as a first step. However, it is not sufficient for claims about empirical relevance or practical measurement. The constructs are latent and the paper does not provide an operational estimation protocol applied to real data, nor does it quantify out‑of‑sample predictive power versus established benchmarks. Below, I discuss appropriateness, sufficiency, and fairness, and then suggest concrete, additional evaluation methods and metrics that could turn the framework into a falsifiable, empirically informative theory.
What is evaluated and how
- Logical consistency and derivability:
- The paper adopts a set of axioms (adapted from Lieb–Yngvason) and shows that, given these axioms, macro‑quantities such as entropy S and temperature T exist and have properties analogous to thermodynamics (monotonicity, concavity, comparative‑statics relations, equilibrium conditions).
- It establishes that definitions of accessibility (X ≼ Y), reversible accessibility (X ∼ Y), and financial equilibrium (X ≡ Y) deliver standard results (e.g., pre‑order properties; equivalence relations; non‑decrease of entropy in allowed transitions; conditions for money flow).
- Constructive examples:
- A “toy” micro‑founded exchange economy (Cobb–Douglas) is used to compute an explicit entropy and to illustrate model mechanics.
- Relation to known results:
- The theory recovers macro analogues of classical comparative‑statics results (macro Slutsky symmetry, Le Chatelier–Samuelson), defines “values” of goods and conditions for trade, introduces “money capacity,” and outlines a Carnot‑like cycle.
These are all internal, coherence‑based checks; they do not involve empirical validation within this paper.
Appropriateness
- For an axiomatic framework, the chosen methodology is appropriate:
- The paper builds on a well‑specified formal structure (Lieb–Yngvason) and embraces the discipline of making assumptions explicit (e.g., A0 unique statistical equilibrium; indecomposability; transitivity of financial equilibrium).
- It clarifies the economic reading of thermodynamic primitives and delivers testable qualitative predictions (direction of money flows by temperature gradients; entropy increase along accessible transitions; equilibrium conditions as equality of temperatures).
- Using a tractable micro example (Cobb–Douglas) to compute S and verify concavity is a sensible constructive validation step.
Sufficiency
- For claims of internal coherence: largely sufficient. The mapping to axioms is explicit; results are logically derived; the toy model works as a consistency check.
- For claims of empirical relevance and measurement: not yet sufficient.
- The constructs S (aggregate utility/entropy) and T (inverse marginal aggregate utility of money) are latent; practical identification/measurement is not demonstrated.
- No empirical benchmarks are used to contrast TM’s predictive power vis‑à‑vis conventional models (e.g., DSGE, gravity models, money demand).
- Robustness to violations of key axioms (e.g., non‑uniqueness of statistical equilibrium, decomposability, frictions, capital controls) is not stress‑tested with data.
Fairness
- The paper candidly discusses limitations (exchange‑only economies, extensivity, uniqueness of equilibrium) and points to future work (production/consumption, non‑equilibrium).
- It fairly situates itself relative to Samuelson, econophysics, and thermoeconomics, and is careful not to overclaim micro‑foundations.
- Some strong assumptions (A0 uniqueness/ergodicity; indecomposability; transitivity of financial equilibrium implying no cyclic net flows) are acknowledged but could use deeper empirical scrutiny, because they are critical for many results and may be fragile in real economies.
Gaps and risks
- Identifiability: Without a practical protocol for measuring T and S, empirical testing is hard; the “thermometer” idea needs to be operationalized.
- External validity: Real economies feature frictions, transaction costs, capital controls, credit/finance, and production. These can violate accessibility assumptions and equivalence properties, changing the direction/size of flows or even forbidding contact states.
- Multiple equilibria and path dependence: The assumption of a unique statistical equilibrium (A0) is a strong and potentially violated premise in macro/finance data (herding, coordination failures, segmentation).
- Cyclic flows: The transitivity of financial equilibrium implies no net cyclic flows at equilibrium; yet in data, cyclic remittances/investment chains can persist, challenging this axiom or its domain of applicability.
Suggested additional evaluation methods and metrics
To move from a coherent axiomatization to a testable empirical framework, the following evaluation strategies and metrics would be valuable.
1) Operationalize temperature and entropy
Provide one or more concrete measurement protocols:
- Exchange‑based thermometer:
- Define a small, standardized, reversible test trade between the target economy and a reference “thermometer” economy; infer T from the money transfer at zero net “value” change.
- Metric: estimated T with confidence intervals; test reproducibility across test bundles and contact mechanisms.
- Money‑demand‑based proxy:
- If is the marginal aggregate utility of money, use an estimated money demand or liquidity services model to infer ; map to T via a calibrated utility system.
- Metrics: cross‑sectional and time‑series stability of T, sensitivity to model specification.
- Price‑level proxy:
- Explore whether T is proportional to a theoretically grounded price level or real balance measure (beyond arbitrary baskets) by deriving conditions under which .
- Metric: fit of T proxies against observed money flow directions across economies.
2) Directional tests of money flows under financial contact
Use natural experiments where financial contact changes exogenously:
- Cases: entry into/removal from currency unions (euro adoption), capital account liberalization episodes, relaxation of remittance restrictions, mobile‑money corridor openings.
- Predictions:
- Sign test: net money flows should go from higher T to lower T upon opening contact.
- Magnitude test: flow intensities correlate with |ΔT| and “money capacity.”
- Metrics:
- Directional accuracy (% of cases where sign is correctly predicted).
- Rank correlation or regression coefficients of net flows on ΔT, controlling for standard determinants (interest differentials, risk, PPP gaps).
- Out‑of‑sample hit rates versus benchmarks (e.g., models with interest rate parity alone).
3) Comparative statics and symmetry tests
Empirically test macro analogues of Slutsky symmetry and Le Chatelier–Samuelson:
- Estimate an aggregate demand system across major good categories using national accounts or household survey data (e.g., AI‑DS or translog at the macro level).
- Test symmetry and negative semi‑definiteness of cross‑derivatives implied by the concavity of S in the TM framework.
- Metrics:
- Wald tests for symmetry restrictions.
- Frequency and magnitude of violations across countries/time.
- Comparison with standard demand system estimates to assess incremental validity.
4) Money capacity estimation
Define and estimate “money capacity” (response of T or “value of money” to money injections):
- Use identified monetary policy shocks (e.g., Romer–Romer, high‑frequency identification) and measure the impulse response of T (or its proxy).
- Metrics:
- Estimated dT/dM (or elasticity d log T/d log M) across regimes.
- Stability across monetary policy episodes (e.g., QE vs. normal times).
- Forecast performance for inflation or money value changes versus standard models.
5) Carnot‑cycle and arbitrage bounds
If the theory yields a bound on profits from cycles based on temperature ratios:
- Construct portfolios or trade cycles that mimic the proposed Carnot logic across partially integrated markets (e.g., wholesale‑retail price gaps, cross‑border e‑commerce with frictions).
- Metrics:
- Realized profit rates vs. TM’s theoretical bound.
- Frequency of bound violations after costs; relation to ΔT.
6) Agent‑based and micro‑founded simulations
Complement LMC by stress‑testing assumptions:
- Simulate economies with:
- Multiple equilibria/herding to assess the impact of A0 violations.
- Frictions/capital controls to paper deviations from predicted flows.
- Non‑extensivity (“lumpiness”) to test robustness of concavity and additivity.
- Metrics:
- Entropy monotonicity under accessible transitions.
- Recovery of T from simulated thermometer trades.
- Degradation of predictions as axioms are relaxed.
7) Event studies of liberalization and integration
- Examine entropy changes before/after trade or financial liberalizations.
- Metrics:
- Estimated change in S (or proxy) post‑event; placebo tests.
- Whether mutually beneficial trades (entropy increasing for all parties) are observed more often than not.
Practical considerations for measurement
- Identification challenges: S and T are cardinal and economy‑level; careful normalization is needed (e.g., invariance to units/numeraire scaling).
- Data sources: balance of payments (net transfers/remittances), monetary aggregates, price levels, national accounts, micro household expenditure surveys, financial frictions indices, policy event chronologies.
- Benchmarks: Compare to gravity models (for flows), UIP/PPP gaps (for prices/flows), standard money demand (for money value), and DSGE impulse‑response predictions.
Summary
- The paper’s current evaluation is appropriate for a foundational axiomatic theory: it demonstrates internal coherence, derives testable qualitative predictions, and provides illustrative examples. For claims about empirical relevance, however, it is not yet sufficient.
- To make the framework empirically meaningful and falsifiable, the authors should:
- Operationalize and estimate temperature and entropy with clear, reproducible protocols.
- Test directional and quantitative predictions of money flows when financial contact changes.
- Empirically assess the macro Slutsky symmetry and money capacity.
- Benchmark predictive performance against standard models.
- Stress‑test axioms via simulations and natural experiments, especially under frictions and potential multiple equilibria.
- These additions would provide a fair and rigorous evaluation of Thermal Macroeconomics as a candidate macroscopic theory of exchange economies.
Comparison with Prior Architectures
Comparative Analysis of the Paper’s Method Against Well‑Known Macroeconomic “Architectures”
What the paper proposes (in brief)
The paper advances Thermal Macroeconomics (TM), an axiomatic, purely macro-level framework that maps the mathematical structure of classical thermodynamics (in Lieb–Yngvason’s axiomatization) to exchange economies. It introduces aggregate state variables—economic entropy (a cardinal “aggregate utility”), temperature (the inverse of the marginal aggregate utility of money), money capacity, and the “value” of goods—to derive a second law for macro transitions (allowed transitions satisfy ), equilibrium conditions, and comparative statics without microfoundations. Prices and the value of money are obtained via reversible trade and financial equilibrium, independent of utility-maximizing agents and without reliance on a basket-of-goods numeraire.
Side‑by‑side comparison with prior architectures
The following table positions the paper’s method against canonical macro frameworks and nearby thermodynamic analogies.
| Framework | Level of analysis | Core primitives | Equilibrium concept | Treatment of money | Prices and cross-derivatives | Core laws/constraints | Methodological stance | Scope limits |
|---|---|---|---|---|---|---|---|---|
| Thermal Macroeconomics (this paper) | Purely macro (aggregate states) | Extensive exchange systems; accessibility preorder; financial equivalence; , , money capacity | Statistical equilibrium; financial equilibrium via money flow; second-law admissibility | Money is conserved and is the analog of energy; “temperature” satisfies | Prices derived from “values” via reversible trade; recovers Slutsky symmetry and Le Chatelier-Samuelson at macro level | Second law: feasible transitions satisfy ; concavity of ; extensivity | Axiomatic, thermodynamics‑inspired; no microfoundations; relies on Lieb–Yngvason structure | Exchange economies only; assumes unique statistical equilibrium, extensivity, and (financial) indecomposability |
| Arrow–Debreu GE | Micro-founded (agents, preferences) | Ordinal utilities, endowments, technology | Static competitive equilibrium (market clearing) | Numeraire/basket normalizations; no intrinsic “temperature” | Slutsky, Hotelling, and comparative statics from individual optimization | Existence/uniqueness under convexity/continuity | Deductive microfoundations; welfare theorems | No dynamics; prices/value of money normalized not derived |
| DSGE (RBC/New Keynesian) | Micro-founded dynamic | Intertemporal utility/profit maximization; shocks | Rational expectations equilibrium (stochastic) | Money via monetary frictions (cash-in-advance, pricing, etc.) | Cross-derivatives from optimizing agents; calibration/estimation | Budget constraints, Euler conditions | Structural, calibration/estimation heavy | Relies on strong rationality and representative-agent simplifications |
| Stock–Flow Consistent (SFC) | Macro accounting | Sectoral balance sheets and transaction matrices | Accounting-consistent steady states/dynamics | Endogenous money creation; detailed financial circuits | Comparative statics from closures/behavioral rules | Accounting identities; stock–flow consistency | Empirical/structural; behavioral equations | Requires behavioral closures; no entropy/second-law constraint |
| Agent‑Based Models (ABM) | Micro to macro emergence | Heterogeneous interacting agents | Emergent/statistical equilibria | Money per institutional rules | Prices emerge via market microstructure | No universal macro law; simulation‑based | Computational, bottom-up | Hard to generalize analytically |
| Econophysics (statistical mechanics) | Macro/statistical | Distributions, kinetic exchange, scaling | Stationary distributions; often non‑equilibrium | Money/wealth as conserved/flow variables in stylized models | Empirical regularities (tails, scaling) | Conservation in stylized exchange; entropy maximization heuristics | Data‑driven/stat-mech analogies | Often lacks institutional economic mapping |
| Samuelson’s thermodynamic analogies | Micro comparative statics | Utility maximization; duality | Static optimum | Money as numeraire or via specific frictions | Hotelling/Samuelson relations; curvature/symmetry | Mathematical isomorphisms (optimization ↔ thermodynamics) | Analogical; skeptical about entropy in economics | Agent-level; no macro entropy/second law |
| Georgescu‑Roegen, thermoeconomics | Macro/ecological | Physical entropy; energy/exergy | Physical feasibility | Money subordinate to physical constraints | Not central | 2nd law of physics constrains economy | Physicalist constraints on growth | Different domain: physical thermodynamics, not economic macro entropy |
Similarities
- With Arrow–Debreu and Samuelson: Shares a rigorous axiomatic spirit and derives comparative statics (e.g., Slutsky symmetry, Le Chatelier–Samuelson) but obtains them at the macro level without agent optimization.
- With DSGE: Embraces equilibrium as an organizing concept; however, equilibrium here is statistical (ergodic stationary distributions), not a fixed point of optimizing agents.
- With SFC: Emphasizes conservation (of money, goods) and the primacy of aggregate stocks/flows; but imposes a thermodynamic-style feasibility constraint (second law) rather than behavioral closures.
- With Econophysics: Imports tools from physics; but this work follows classical thermodynamics via Lieb–Yngvason axioms rather than statistical mechanics or kinetic exchange models.
Differences
- Foundational stance: Dispenses with microfoundations. Aggregate regularities (prices, money’s value, trade directions) are deduced from macro axioms, not from preferences, information, or strategic behavior.
- Cardinal macro utility: Introduces a cardinal aggregate quantity, economic entropy , rather than ordinal utilities; governs feasibility of transitions via .
- Temperature of money: Defines an economy’s temperature as the inverse marginal aggregate utility of money, . Money flows from low to high inverse marginal utility (high to low ), clarifying financial equilibrium as under financial contact.
- Price and value without baskets: Derives the value of money and market prices via reversible trade and “values” of goods; avoids arbitrary basket normalizations and numeraire artifacts.
- Accessibility and equivalence: Organizes macro transitions through an accessibility preorder () and a financial-equivalence relation (), enabling a precise second-law statement for economic state changes.
- Non-equilibrium potential: By starting from the thermodynamic structure (not microfoundations), the framework is poised to extend to nonequilibrium macro (e.g., flux-driven cycles) analogously to non-equilibrium thermodynamics, beyond DSGE’s shock-driven dynamics.
Concrete innovations
- A second law for macroeconomics: Admissible transitions across systems or through trade satisfy , yielding quantitative trade conditions and a principled direction for money flow under financial contact.
- Economic temperature and money capacity: New macro state variables with operational interpretations; the paper outlines a “thermometer” to measure .
- Carnot-style arbitrage: A macro analogue of the Carnot cycle shows how traders can extract profit from temperature differences, complementing price-difference arbitrage.
- Macro Slutsky/Le Chatelier without micro rationality: Symmetry and negative definiteness of a macro Slutsky matrix, and Le Chatelier–Samuelson, follow from the concavity of and the axioms.
- Value of money without a consumption basket: The value emerges from state variables and reversible trade, not from an exogenous CPI-like construction.
- “Pure money” and extensivity: Formalizes the role of money as an extensive quantity and examines cases where it carries no intrinsic utility apart from exchange facilitation.
Limitations relative to extant frameworks
- Scope restrictions: Focuses on extensive exchange economies—no production, consumption, labor, credit creation dynamics, or policy rules yet. DSGE, SFC, and ABM address many of these directly.
- Equilibrium assumptions: Relies on unique statistical equilibrium (ergodicity/indecomposability) and extensivity; real economies may violate these via herding, segmentation, institutional frictions, or increasing returns.
- Measurement and identification: While the paper proposes a way to measure , empirical implementation and identification of at scale remain open, whereas DSGE/SFC have established estimation/calibration traditions.
- Money and finance: Treats money as conserved at the system boundary; endogenous money creation, leverage, and credit cycles (central to SFC and modern macrofinance) are slated for future extensions.
Is the method evolutionary or revolutionary?
- Evolutionary in results: Many comparative-static regularities (e.g., Slutsky symmetry, Le Chatelier–Samuelson, existence of prices) reappear, but they are derived from different premises. The framework thus recovers and reframes familiar macro relations.
- Revolutionary in foundations and concepts: The pivot to a macro-axiomatic, thermodynamics-based structure—introducing a cardinal macro entropy , an economic temperature , a second law governing feasible transitions, and pricing/value derived from reversible trade—constitutes a paradigm shift relative to micro-founded general equilibrium and DSGE. It also departs meaningfully from earlier thermodynamic analogies (Samuelson) and from ecological “thermoeconomics” (Georgescu–Roegen).
Overall, the paper’s approach is best described as conceptually revolutionary but substantively connective: it preserves key comparative statics known from micro-founded architectures while proposing a new, thermodynamically grounded macro “architecture” that does not rely on rational-agent microfoundations and that naturally invites extensions to non-equilibrium macro phenomena.
Minimal formal snapshot
- Second law (economic): admissible transitions satisfy .
- Economic temperature: , so financial equilibrium between and implies when in financial contact.
- Concavity: is concave in extensive variables, yielding symmetry/negative definiteness of macro cross-derivatives (macro Slutsky) and a macro Le Chatelier–Samuelson principle.
- Prices via reversible trade: Market prices emerge from “values” consistent with reversibility, tying relative prices to state variables and rather than to arbitrary basket normalizations.
In sum, the paper introduces a new macro-thermodynamic architecture that re-derives familiar comparative statics, explains money’s value and trade direction via temperature and entropy, and sets the stage for a non-equilibrium macro theory rooted in thermodynamic reasoning.
Collections
Sign up for free to add this paper to one or more collections.
