Sequential Learning in the Dense Associative Memory (2409.15729v2)
Abstract: Sequential learning involves learning tasks in a sequence, and proves challenging for most neural networks. Biological neural networks regularly conquer the sequential learning challenge and are even capable of transferring knowledge both forward and backwards between tasks. Artificial neural networks often totally fail to transfer performance between tasks, and regularly suffer from degraded performance or catastrophic forgetting on previous tasks. Models of associative memory have been used to investigate the discrepancy between biological and artificial neural networks due to their biological ties and inspirations, of which the Hopfield network is the most studied model. The Dense Associative Memory (DAM), or modern Hopfield network, generalizes the Hopfield network, allowing for greater capacities and prototype learning behaviors, while still retaining the associative memory structure. We give a substantial review of the sequential learning space with particular respect to the Hopfield network and associative memories. We perform foundational benchmarks of sequential learning in the DAM using various sequential learning techniques, and analyze the results of the sequential learning to demonstrate previously unseen transitions in the behavior of the DAM. This paper also discusses the departure from biological plausibility that may affect the utility of the DAM as a tool for studying biological neural networks. We present our findings, including the effectiveness of a range of state-of-the-art sequential learning methods when applied to the DAM, and use these methods to further the understanding of DAM properties and behaviors.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of concrete gaps and unresolved questions that future work could address to build on this paper’s investigation of sequential learning in Dense Associative Memory (DAM).
- Empirical results missing: The paper outlines methods and design but does not report quantitative outcomes (e.g., accuracy/F1 curves, forgetting metrics, error bars), preventing reproducibility and comparative evaluation.
- Variance and stability not assessed: No mention of multiple random seeds, confidence intervals, or statistical tests; robustness to initialization and data sampling remains unknown.
- Short task sequences: Experiments are limited to five tasks due to training instability; it is unclear how to stabilize DAM for longer sequences (optimizer choice, momentum schedules, gradient clipping, normalization, temperature annealing, memory vector scaling).
- Task-identity leakage: Inputs include a one-hot task ID, effectively operating in a Task-IL setting; performance under more challenging Domain-IL and Class-IL settings (no task labels at test time) is not evaluated.
- Dataset diversity: Only Permuted MNIST (and possibly Rotated MNIST) are considered; behavior on more complex visual or NLP continual learning benchmarks (Split CIFAR-10/100, CUB/AWA, Wiki-30K, Reuters) is untested.
- Task relatedness and transfer: Forward transfer, backward transfer, and zero-shot performance—highlighted as biological desiderata—are not explicitly measured (e.g., using BWT/FWT metrics), especially across tasks with controllable relatedness.
- Continuous-valued and attention-equivalent variants: Findings are limited to binary DAM; it is unknown whether conclusions transfer to continuous modern Hopfield networks and attention-equivalent formulations.
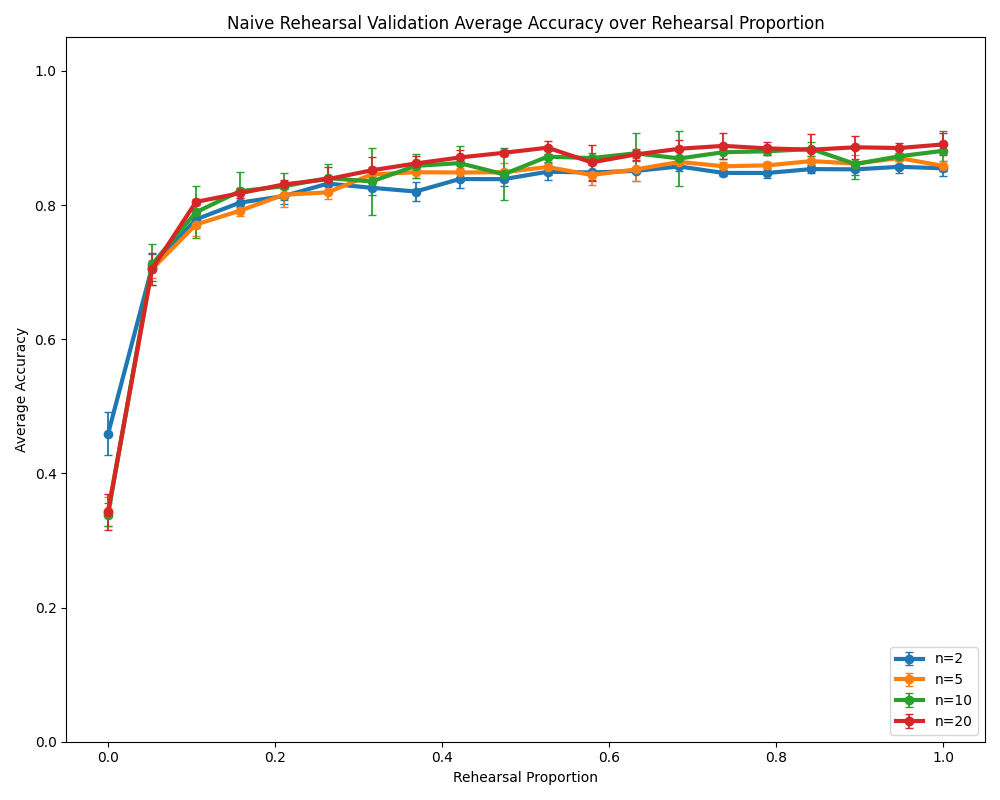
- Interaction vertex n: Although the paper motivates analyzing low vs high n, a systematic mapping of n to forgetting, transfer, and pseudorehearsal efficacy (and to the feature–prototype transition) is not presented.
- Interaction function choices: Only a leaky rectified polynomial with fixed ε=1e-2 is used; the impact of alternative interaction functions and ε on stability, capacity, and forgetting is unexplored.
- Relaxation dynamics: The classifier setup updates only the class neurons and only once; the effect of full attractor relaxation (until convergence), partial updates, and update schedules on forgetting and transfer is not studied.
- Base loss specification: The exact loss used for classification (cross-entropy vs MSE) and the role of the “error exponent m” are not clearly defined; sensitivity of results to loss functions remains unknown.
- Capacity under continual learning: Theoretical capacity scaling with n is cited, but how sequential loading of multiple tasks interacts with capacity (e.g., graceful vs catastrophic degradation as memory vectors are saturated) is not analyzed.
- Memory vector allocation: A fixed 512 memory vectors are used; the trade-off between vector count, task count/size, and forgetting, as well as strategies for dynamic memory growth or task-specific allocation/gating, are unaddressed.
- Architectural CL methods in DAM: Beyond rehearsal/regularization, DAM-specific architectural strategies (freezing subsets of memory vectors, task-aware routing, orthogonalization/gradient isolation across vectors) are not explored.
- Rehearsal scheduling and selection: Only a growing buffer with naive mixing is used; the efficacy of coreset selection, reservoir sampling, class-balancing, sweep rehearsal variants, and curriculum-based buffer scheduling in DAM is unknown.
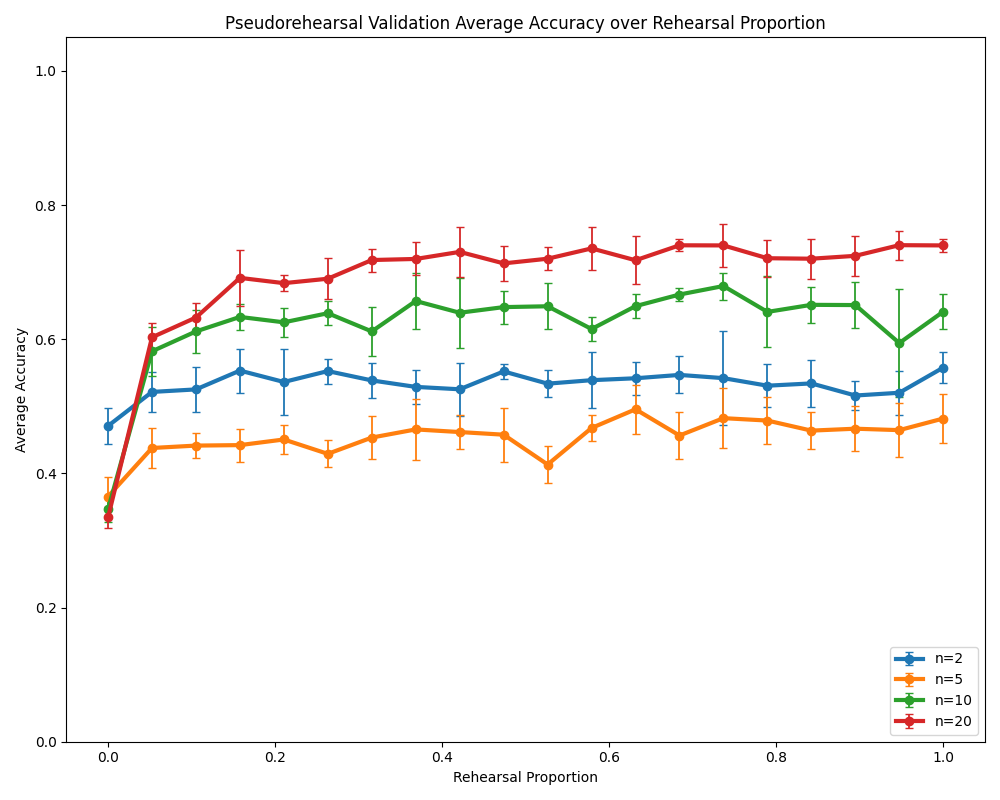
- Pseudorehearsal variants: Only homogeneous pseudorehearsal is implemented; comparison to heterogeneous pseudorehearsal and analysis of probe generation (distribution, noise level, relaxation depth) are missing.
- GEM/A-GEM practicality: While computational caveats are noted, no runtime, CPU–GPU overhead, or memory profiling is reported; scaling behavior with number of tasks/constraints for DAM remains unquantified.
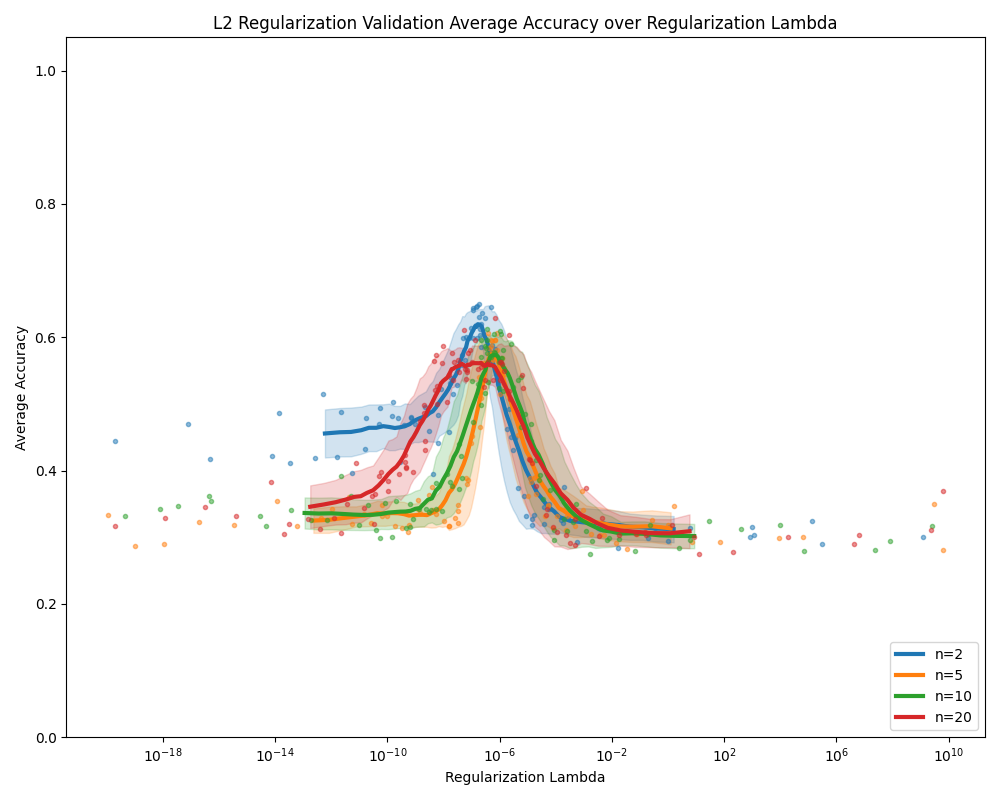
- Regularization in energy-based DAM: EWC/MAS/SI are ported from feed-forward settings, but the best definition of Fisher information, sensitivity, and path-integral importance for DAM’s energy-based dynamics (e.g., computed at attractors vs inputs) is unclear and unvalidated.
- Surrogate loss locality: Quadratic penalties approximate local basins; whether multi-basin solutions exist in DAM for prior tasks and how to regularize toward sets of good solutions (not single points) is not examined.
- Attractor landscape analysis: No visualization or quantitative analysis of energy basins (spurious attractors, basin overlap between tasks, basin volume changes across training) is provided to mechanistically explain forgetting.
- Evaluation metrics breadth: Standard continual learning metrics (average accuracy, backward/forward transfer, average forgetting, intransigence) are not reported; calibration, confidence, and robustness to distribution shifts are not assessed.
- Test-time protocol clarity: With per-task permutations and appended task IDs, the exact test-time pipeline (e.g., availability of task ID) and cross-task evaluation protocol need clarification and ablation.
- Sensitivity to training schedules: The roles of temperature schedule (T_i→T_f), learning rate decay, momentum, batch size, and number of relaxation steps on stability and forgetting are not systematically investigated.
- Comparison to non-DAM baselines: No side-by-side comparison with standard feed-forward or convolutional baselines under identical protocols to isolate any unique advantages or disadvantages of DAM.
- Privacy-preserving replay: Pseudorehearsal is positioned as data-free, but privacy/utility trade-offs vs generative replay (e.g., small VAEs/GANs/flow models) in DAM are not explored.
- Noise and label quality: The impact of label noise, data corruption, or class imbalance on DAM’s sequential learning behavior is untested.
- Reproducibility: Code availability, fixed seeds, and implementation details (e.g., optimizer, gradient clipping, hardware) are not provided; exact hyperparameter ranges for the grid searches are unspecified.
- Bridging to transformers: Although attention–DAM connections are mentioned, the implications for fine-tuning and continual learning in attention modules are not empirically tested or theoretically formalized.
- Theoretical forgetting thresholds: Unlike classical results (e.g., item weight magnitudes and thresholds), there is no analogous theoretical characterization for when DAM undergoes catastrophic forgetting under sequential updates.
Collections
Sign up for free to add this paper to one or more collections.