Self-adaptive weights based on balanced residual decay rate for physics-informed neural networks and deep operator networks (2407.01613v1)

Abstract: Physics-informed deep learning has emerged as a promising alternative for solving partial differential equations. However, for complex problems, training these networks can still be challenging, often resulting in unsatisfactory accuracy and efficiency. In this work, we demonstrate that the failure of plain physics-informed neural networks arises from the significant discrepancy in the convergence speed of residuals at different training points, where the slowest convergence speed dominates the overall solution convergence. Based on these observations, we propose a point-wise adaptive weighting method that balances the residual decay rate across different training points. The performance of our proposed adaptive weighting method is compared with current state-of-the-art adaptive weighting methods on benchmark problems for both physics-informed neural networks and physics-informed deep operator networks. Through extensive numerical results we demonstrate that our proposed approach of balanced residual decay rates offers several advantages, including bounded weights, high prediction accuracy, fast convergence speed, low training uncertainty, low computational cost and ease of hyperparameter tuning.

• The paper demonstrates that discrepancies in inverse residual decay rates lead to training inefficiencies in PINNs and DeepONets.
• It presents a BRDR method that dynamically adjusts loss weights, significantly enhancing convergence speed and prediction accuracy.
• Comparative experiments on benchmark PDEs show that BRDR outperforms methods like soft-attention and residual-based attention.

Self-Adaptive Weights Based on Balanced Residual Decay Rate for Physics-Informed Neural Networks and Deep Operator Networks

Introduction

Physics-informed neural networks (PINNs) and physics-informed deep operator networks (PIDeepONets) are machine learning models designed to integrate physical knowledge directly into their architectures, specifically to solve PDEs. Despite their potential, these models encounter significant challenges in training, especially when facing complex equations characterized by slow convergence and high computational cost.

The paper investigates the underlying reasons for the poor convergence of plain PINNs, identifying significant discrepancies in the convergence speed of residuals at various training points as a primary issue. In response, this work introduces a novel self-adaptive weighting strategy designed to balance the residual decay rate at different training points, enhancing both convergence speed and prediction accuracy.

Understanding the PINN Failure Mechanism

Physics-Informed Neural Networks

PINNs solve PDEs by parameterizing the solution with a neural network and incorporating the physics in the training process. The PINN framework minimizes a loss function composed of both data and physics-based residuals evaluated over collocation points. Despite the theoretical foundation, limitations in the number of collocation points and the approximation capacity often prevent the loss function from achieving an ideal minimum, affecting solution quality.

Training Dynamics in Unweighted PINNs

The training dynamics of an unweighted PINN can be described using the Neural Tangent Kernel (NTK) framework, outlining how the residuals evolve during training. The NTK theory reveals that the convergence rate of different residuals is dictated by the eigenvalues of the NTK, highlighting that slower decaying residuals dominate the overall convergence behavior.

Notably, the paper introduces the concept of the inverse residual decay rate ($irdr$), expressing the relative convergence speed of residuals during training. Disparities in $irdr$ across collocation points can lead to overfitting in regions where residuals decay slower, effectively stalling the overall convergence.

Figure 1: The relationship between inverse residual decay rate $irdr$ and the convergence rate $\lambda$.

Balanced Residual Decay Rate (BRDR) Approach

The BRDR method seeks to dynamically adjust weights in the loss function to reduce convergence disparities. The paper revealed that the slowest residual convergence often governs overall performance. To address this, the BRDR method applies adaptive weighting to equalize these rates. A crucial aspect is the maintenance of unity for the mean weight, ensuring the boundedness and numerical stability of the adaptation process.

Proposed in the paper, the self-adaptive BRDR weighting method allocates increased weights to slow-converging training points on a per-point basis. Essential parameters such as the learning rate ($\eta$), smoothing factors ($\beta_c$, $\beta_w$), and batch size are systematically updated during the training to optimize computation, while maintaining balance in residual decay.

Figure 1: The relationship between inverse residual decay rate irdr and the convergence rate lambda.

Further, for a rigorous assessment, the BRDR method was tested against state-of-the-art adaptive weighting techniques, like the soft-attention (SA) method and residual-based attention (RBA), as applied in the neural network context.

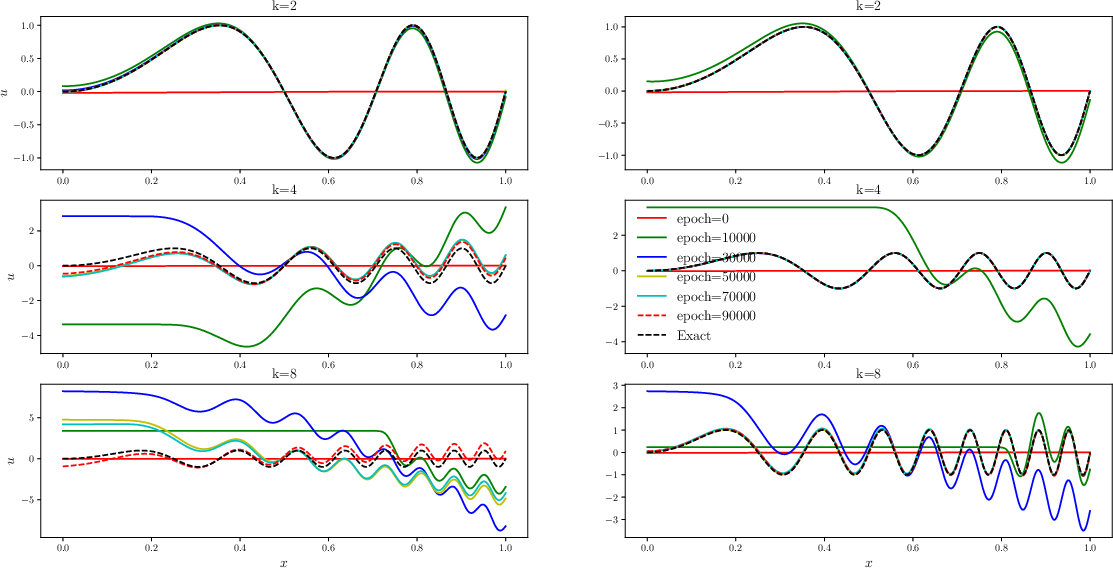
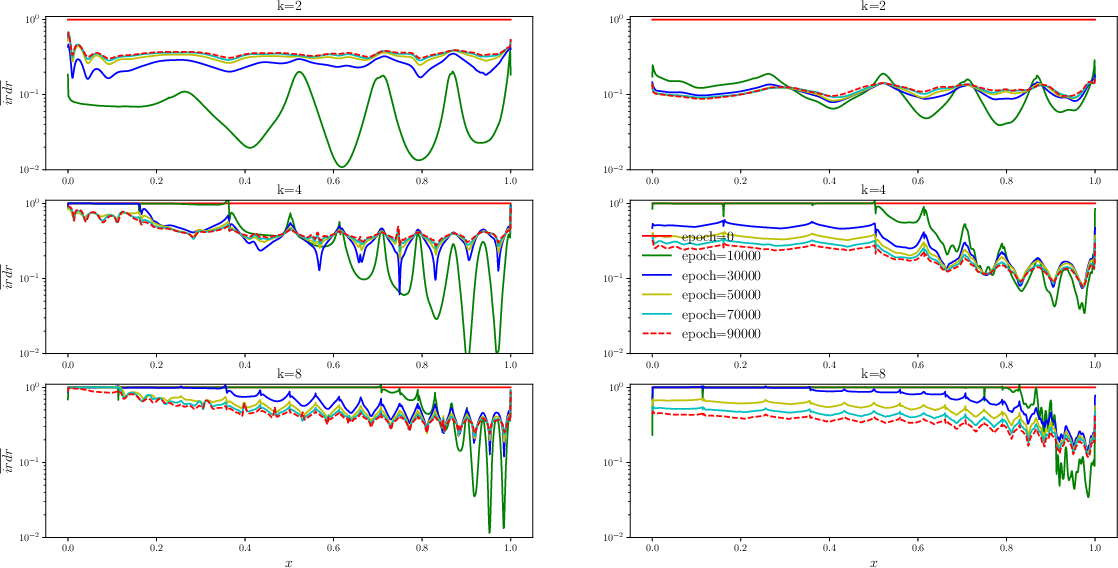
Figure 2: The history of solution and average inverse residual decay rate during training process from plain PINN (left) and BRDR PINN (right). Note that both the plain PINN and BRDR PINN share the same network initialization for the same k.

Evaluations revealed that inverse residual decay rates varied widely across training points, with large discrepancies influencing the convergence speed. Weight adjustment, based on the balanced residual decay rate (BRDR), involves allocating larger weights to points exhibiting slower convergence, thereby equalizing $irdr$ across the domain and speeding up overall model convergence.

Figure 2: The history of solution and average inverse residual decay rate during training process from plain PINN (left) and BRDR PINN (right). Note that both the plain PINN and BRDR PINN share the same network initialization for the same $k$.

The paper introduces a novel point-wise adaptive weighting strategy that addresses these issues, with an update scheme balancing such discrepancies. This method, tested on standard PINN benchmarks like the 2D Helmholtz equation, 1D Allen-Cahn equation, and 1D Burgers equation, yields statistically lower errors and reduced training times across varied complexities of PDEs. A comparative analysis with existing methods—such as Soft-Attention (SA) and Residual-Based Attention (RBA)—demonstrates the superior accuracy and convergence characteristics of the proposed method, particularly when handling distinct components of loss functions like BCs and PDEs.

Figure 2: The history of solution and average inverse residual decay rate during training process from plain PINN (left) and BRDR PINN (right). Note that both the plain PINN and BRDR PINN share the same network initialization for the same k.

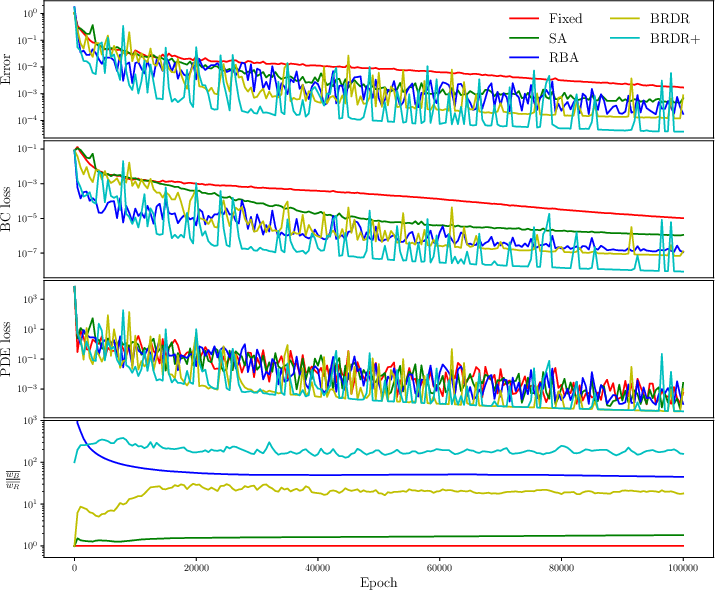
Figure 3: PINN for the 2D Helmholtz equation: The history of $L_2$ relative error, unweighted loss of each component, and the average weight ratio of BC to PDE from fixed-weight training, and adaptive-weight training (SA",RBA", BRDR",BRDR+"). Note that all the cases share the same network architecture and the same random seed for initialization of network parameters.

Implementation-wise, the typical setup for the BRDR method involves well-defined collocation points, specific network architectures like mFCN for PINNs, and mDeepONet architectures for higher-dimensional or operator learning problems. The choice of fixed rates $(\beta_c, \beta_w)$ falls within a narrow range, typically between 0.999 and 0.9999, which alleviates the manual labor generally associated with hyperparameter tuning in other methods.

\subsection{Implications and Future Developments} The adaptive weighting method based on a balanced residual decay rate ($\mathit{BRDR}$) proposed in this paper represents an advancement in training PINNs and PIDeepONets, addressing well-known convergence speed variations at different points in the domain. Its design ensures weight boundedness and allows for straightforward configuration via hyperparameters, reducing the necessity for extensive hyperparameter tuning compared to other existing adaptive methods.

The results compiled in the paper substantiate the enhanced performance of the BRDR method on benchmark problems for rocket surgery-like challenges: the 2D Helmholtz equation for PINNs and PIDeepONets, and the wave and Burgers equations for PIDeepONets. BRDR and its variants outperform the selected state-of-the-art adaptive weighting methods in terms of prediction accuracy, convergence speed, and computational cost, while offering significantly reduced uncertainty.

The implications of this work are twofold: From a practical standpoint, the proposed BRDR method offers a more reliable and efficient option for training physics-informed machine learning models on challenging complex systems. Theoretically, the framework based on balanced convergence speed presents a new paradigm in designing adaptive weighting methods, with potential applications to other deep learning frameworks. The authors suggest that this approach can be further enhanced by incorporating adaptive sampling strategies to overcome the challenge of non-homogeneous error distribution, ensuring more accurate and stable predictions. As the field continues to evolve, such methods hold promise in improving the robustness and efficiency of physics-informed machine learning models, making them more suitable for a wide range of advanced computational problems.

In conclusion, the balanced residual decay rate methodology offers a compelling alternative to existing adaptive weighting strategies, overcoming limitations in convergence speed and computational cost, while providing significant improvements in accuracy and robustness for both PINNs and PIDeepONets. As this field evolves, the integration of BRDR with other advanced methodologies holds the potential for further progress in developing efficient and robust machine learning frameworks for solving complex PDE problems.