DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models

Abstract: Mathematical reasoning poses a significant challenge for LLMs due to its complex and structured nature. In this paper, we introduce DeepSeekMath 7B, which continues pre-training DeepSeek-Coder-Base-v1.5 7B with 120B math-related tokens sourced from Common Crawl, together with natural language and code data. DeepSeekMath 7B has achieved an impressive score of 51.7% on the competition-level MATH benchmark without relying on external toolkits and voting techniques, approaching the performance level of Gemini-Ultra and GPT-4. Self-consistency over 64 samples from DeepSeekMath 7B achieves 60.9% on MATH. The mathematical reasoning capability of DeepSeekMath is attributed to two key factors: First, we harness the significant potential of publicly available web data through a meticulously engineered data selection pipeline. Second, we introduce Group Relative Policy Optimization (GRPO), a variant of Proximal Policy Optimization (PPO), that enhances mathematical reasoning abilities while concurrently optimizing the memory usage of PPO.

• The paper introduces DeepSeekMath, a novel model that excels in mathematical reasoning using math-specific pre-training and the GRPO reinforcement learning algorithm.
• It harnesses a high-quality corpus of 120B math-related tokens, enhancing performance with an efficient iterative data selection process and group-based reward estimation.
• Experimental results demonstrate significant accuracy boosts on benchmarks like MATH and GSM8K, outperforming many open- and closed-source models.

DeepSeekMath: Advancing Mathematical Reasoning in Open LLMs

The paper "DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open LLMs" (2402.03300) presents DeepSeekMath, a novel LLM designed to excel in mathematical reasoning. This model achieves state-of-the-art performance on mathematical benchmarks through a combination of large-scale math-specific pre-training and a novel reinforcement learning algorithm. The key contributions of this work include the creation of a large, high-quality mathematical corpus, the development of an efficient RL method called Group Relative Policy Optimization (GRPO), and a comprehensive analysis of factors influencing mathematical reasoning in LLMs.

Data Collection and Pre-training

A significant aspect of DeepSeekMath is its pre-training on a meticulously curated corpus of 120B math-related tokens. This corpus, termed the DeepSeekMath Corpus, was constructed by iteratively mining Common Crawl data using a fastText-based classifier (Figure 1).

Figure 1: An iterative pipeline refines mathematical web page selection from Common Crawl for high-quality data.

The iterative data selection process involves training a classifier on an initial seed corpus (OpenWebMath) and then using it to identify additional math-related web pages from Common Crawl. Human annotation is employed to further refine the dataset, improving the classifier's performance in subsequent iterations. The resulting corpus is significantly larger than existing math-specific datasets like MathPile and OpenWebMath. Through pre-training experiments, the authors demonstrate that the DeepSeekMath Corpus is of high quality and covers multilingual mathematical content.

Group Relative Policy Optimization

The paper introduces GRPO, a variant of PPO designed to enhance mathematical reasoning abilities while optimizing memory usage. GRPO distinguishes itself from PPO by foregoing the critic model and instead estimating the baseline from group scores (Figure 2).

Figure 2: A comparison between PPO and GRPO highlights GRPO's streamlined approach, estimating baselines from group scores to reduce training resources.

For each question, GRPO samples a group of outputs and uses the average reward of these outputs as the baseline. This approach significantly reduces training resources compared to PPO, which requires training a separate value function.

The authors also explore different variants of GRPO, including outcome supervision and process supervision. Outcome supervision provides a reward at the end of each output, while process supervision provides a reward at the end of each reasoning step. Experimental results indicate that process supervision leads to better performance, suggesting that fine-grained feedback is beneficial for mathematical reasoning. Furthermore, iterative RL with GRPO is explored, where the reward model is continuously updated based on the policy model's sampling results.

Experimental Results

The effectiveness of DeepSeekMath is demonstrated through extensive experiments on a range of mathematical benchmarks. The base model, DeepSeekMath-Base 7B, achieves a top-1 accuracy of 36.2% on the competition-level MATH dataset, surpassing Minerva 540B and other open-source base models (Figure 3).

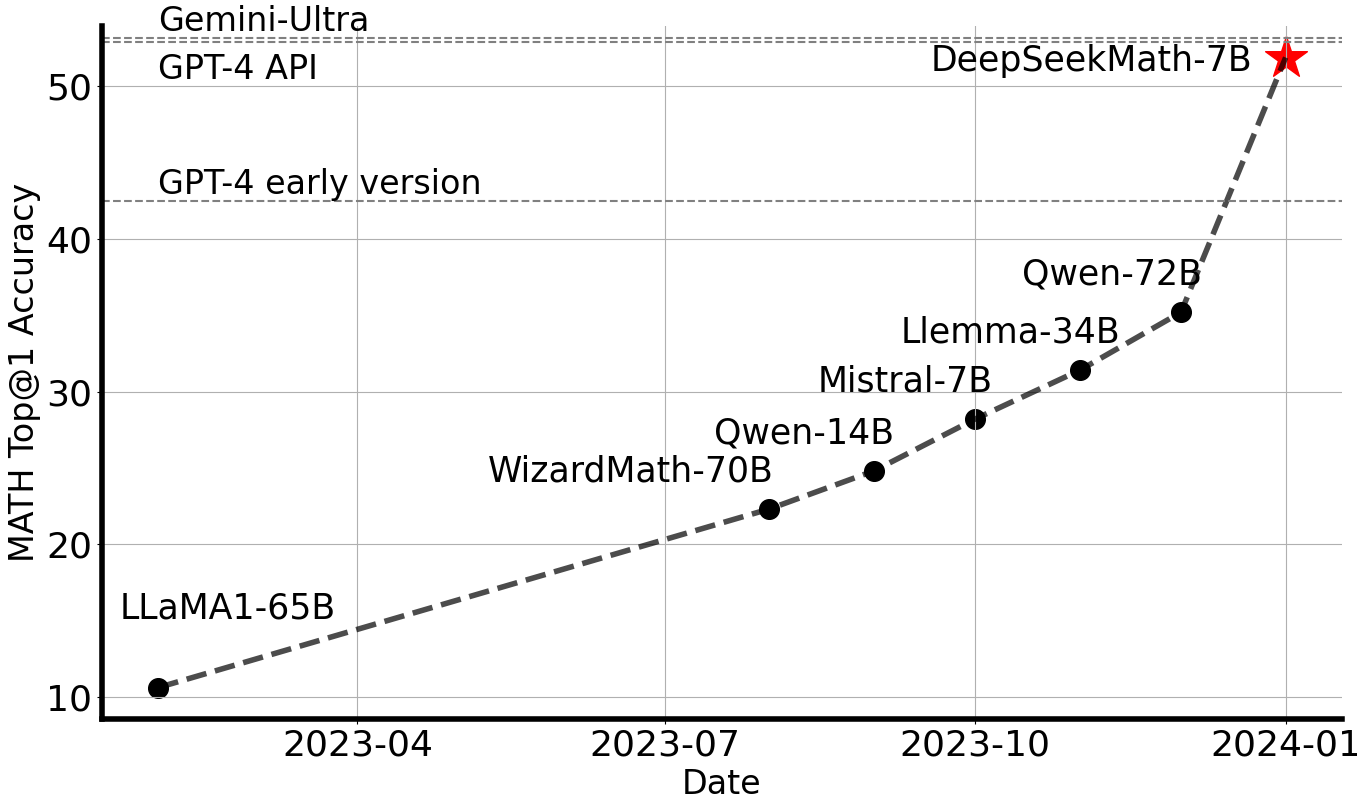
Figure 3: A graph compares the top-1 accuracy of various open-source models on the challenging MATH benchmark.

After instruction tuning, DeepSeekMath-Instruct 7B achieves 46.8% accuracy on MATH, which is further improved to 51.7% through reinforcement learning with GRPO. The authors also evaluate the model's performance on other mathematical reasoning benchmarks, such as GSM8K, SAT, C-Math, and Gaokao, demonstrating its strong generalization ability. The instruction-tuned and RL-optimized models beat all open-source models from 7B to 70B, as well as the majority of closed-source models. The benefits of RL are showcased in Figure 4 and Figure 5.

Figure 4: A performance comparison of the DeepSeekMath-Instruct 1.3B model after training with different methods on GSM8K and MATH benchmarks.

Figure 5: Performance gains from iterative reinforcement learning with DeepSeekMath-Instruct 7B on GSM8K and MATH benchmarks.

Analysis and Discussion

The paper also provides a detailed analysis of factors influencing mathematical reasoning in LLMs. The authors find that code training prior to math training improves models' ability to solve mathematical problems, both with and without tool use. However, contrary to common belief, training on arXiv papers does not lead to notable improvements on mathematical benchmarks.

The authors provide a unified paradigm to analyze different training methods, such as SFT, RFT, DPO, PPO, and GRPO. This paradigm conceptualizes all these methods as either direct or simplified RL techniques. Based on this unified view, the authors explore the reasons behind the effectiveness of reinforcement learning and summarize potential directions for achieving more effective RL of LLMs. RL is shown to primarily enhance the Maj@K performance, rendering the output distribution more robust (Figure 6).

Figure 6: This graph depicts the Maj@K and Pass@K metrics for SFT and RL-enhanced DeepSeekMath 7B on GSM8K and MATH datasets.

Conclusion

The DeepSeekMath paper makes significant contributions to the field of mathematical reasoning in LLMs. The creation of a large, high-quality math corpus and the development of the GRPO algorithm are valuable advancements. The analysis of factors influencing mathematical reasoning provides insights for future research in this area. While DeepSeekMath achieves impressive results on quantitative reasoning benchmarks, the authors acknowledge limitations in geometry and theorem proving. Future work will focus on improving data selection, exploring more effective RL techniques, and scaling up the model size.