How Much Training Data is Memorized in Overparameterized Autoencoders? An Inverse Problem Perspective on Memorization Evaluation (2310.02897v2)

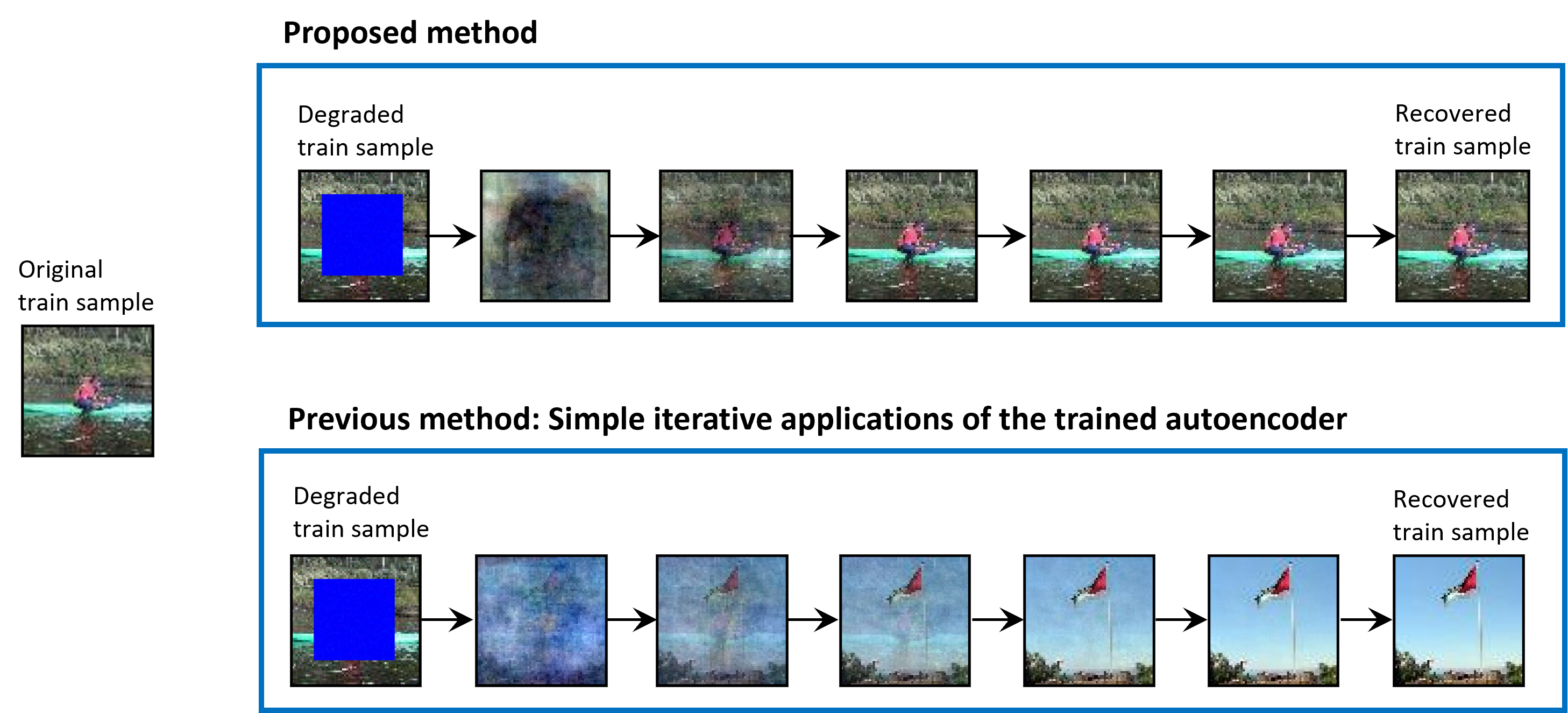
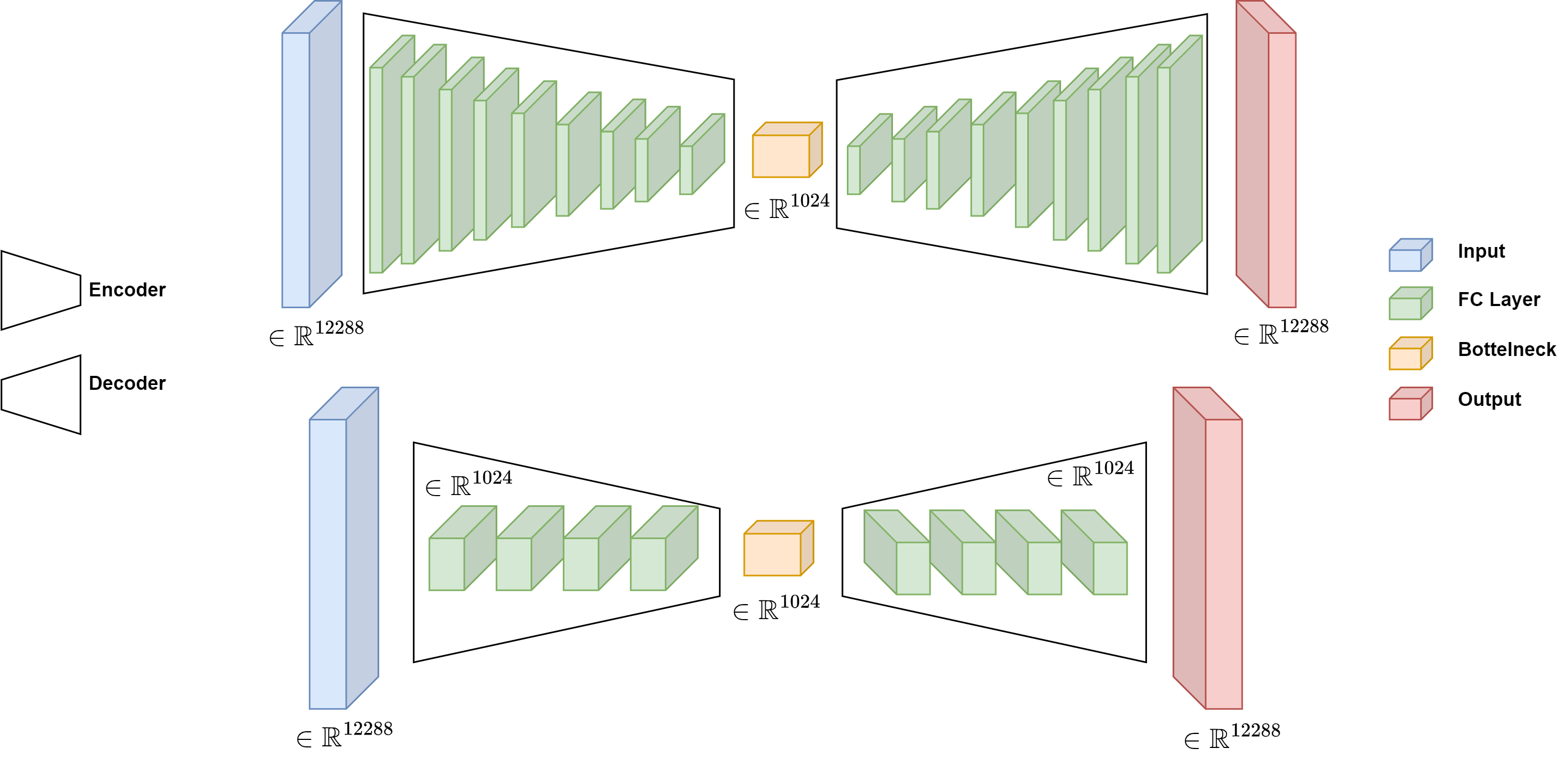
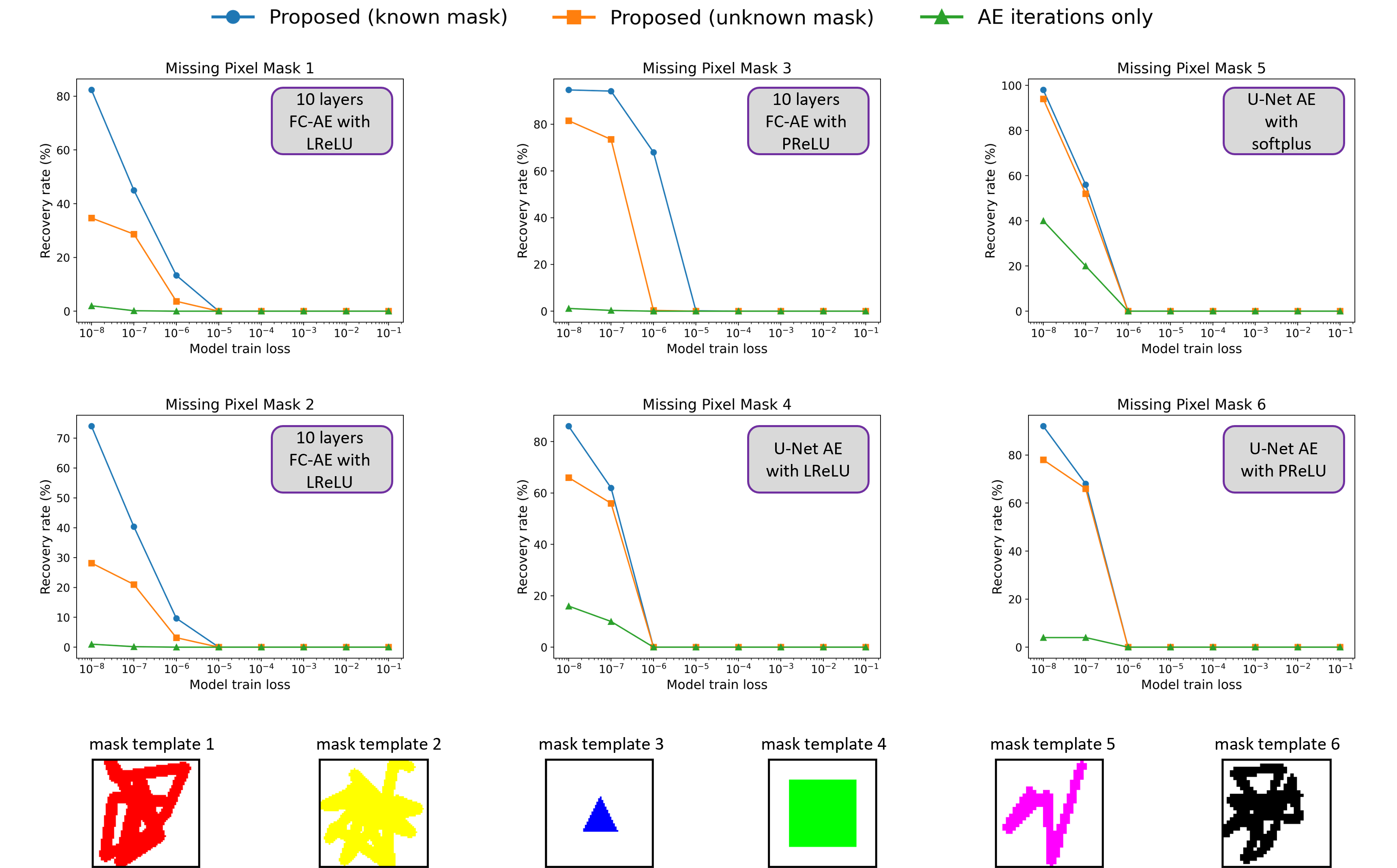
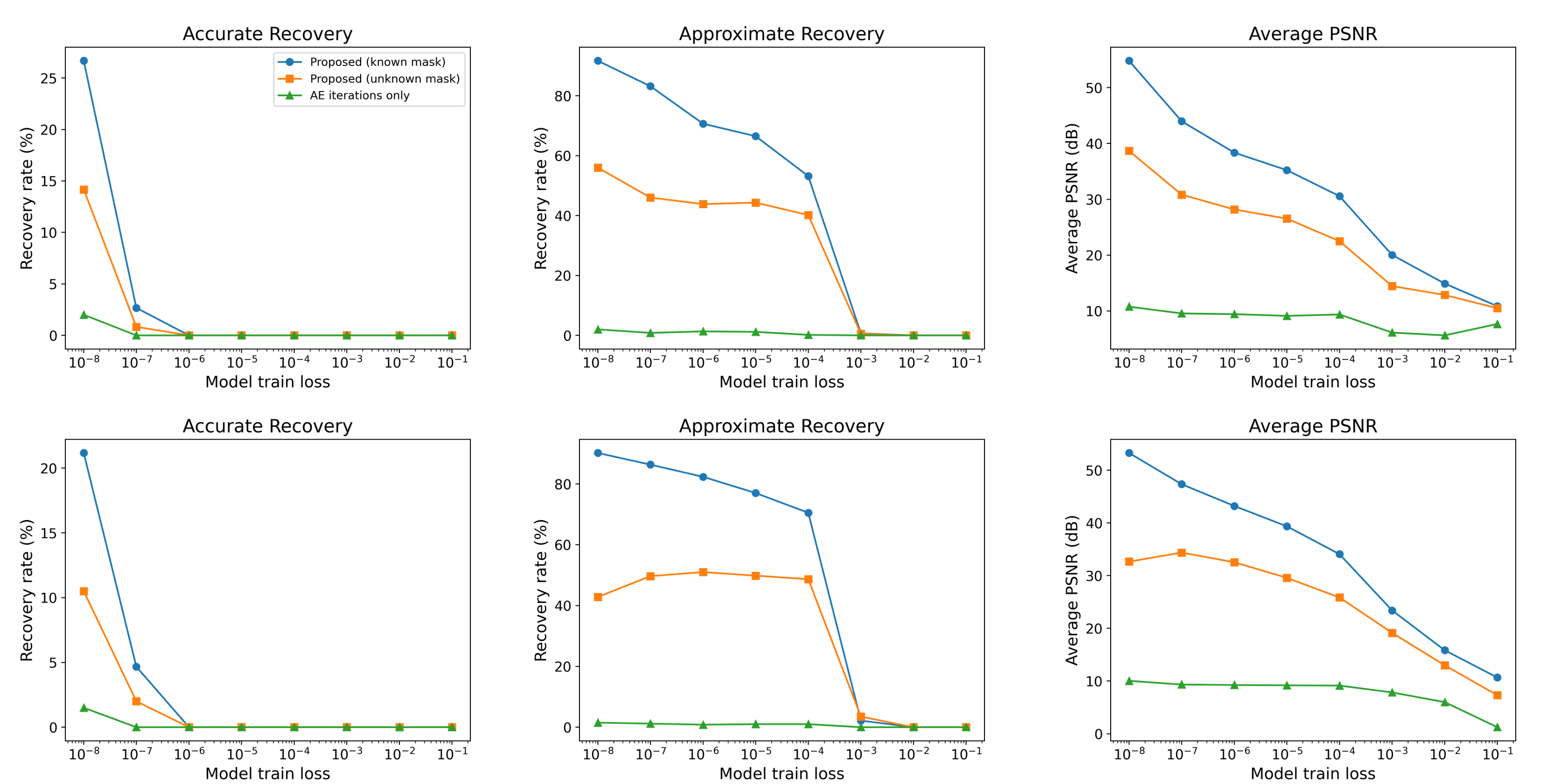
Abstract: Overparameterized autoencoder models often memorize their training data. For image data, memorization is often examined by using the trained autoencoder to recover missing regions in its training images (that were used only in their complete forms in the training). In this paper, we propose an inverse problem perspective for the study of memorization. Given a degraded training image, we define the recovery of the original training image as an inverse problem and formulate it as an optimization task. In our inverse problem, we use the trained autoencoder to implicitly define a regularizer for the particular training dataset that we aim to retrieve from. We develop the intricate optimization task into a practical method that iteratively applies the trained autoencoder and relatively simple computations that estimate and address the unknown degradation operator. We evaluate our method for blind inpainting where the goal is to recover training images from degradation of many missing pixels in an unknown pattern. We examine various deep autoencoder architectures, such as fully connected and U-Net (with various nonlinearities and at diverse train loss values), and show that our method significantly outperforms previous memorization-evaluation methods that recover training data from autoencoders. Importantly, our method greatly improves the recovery performance also in settings that were previously considered highly challenging, and even impractical, for such recovery and memorization evaluation.

• The paper introduces an inverse problem strategy to evaluate memorization by recovering degraded training images using overparameterized autoencoders.
• The paper leverages ADMM and plug-and-play priors to optimize both reconstruction and degradation estimation, outperforming existing methods.
• The paper demonstrates robust recovery and noise resilience across multiple architectures, including fully connected models and U-Net designs.

How Much Training Data is Memorized in Overparameterized Autoencoders? An Inverse Problem Perspective on Memorization Evaluation

Introduction

The paper investigates the phenomenon of memorization in overparameterized autoencoders, focusing on their ability to reconstruct degraded training images. The authors propose an inverse problem perspective, where the recovery of a degraded training image is formulated as an optimization task, using the trained autoencoder to implicitly define a regularizer for the dataset. This approach is tested on various architectures, demonstrating superior performance compared to previous methods.

Inverse Problem Formulation

The core contribution of the paper is the reframing of memorization as an inverse problem. Given a degraded training image, the objective is to recover the original image by minimizing a cost function that balances the reconstruction error and a regularization term. This regularization is implicitly defined by the trained autoencoder, reflecting the degree of memorization inherent in the model.

Figure 1: Iterative recovery of a degraded training image using our proposed approach (top frame) and the method from previous works (bottom frame).

Implementation Details

Algorithmic Approach

The proposed method leverages the Alternating Direction Method of Multipliers (ADMM) combined with plug-and-play priors. The ADMM decomposition enables separate optimization of the image reconstruction and the estimation of the degradation operator. Notably, the framework extends the plug-and-play paradigm, traditionally used with denoisers, to incorporate arbitrary autoencoders.

Architectural Considerations

Experiments are conducted on fully connected and U-Net autoencoders with various nonlinearities. The architectures include:

1. Fully Connected Autoencoders: 10 and 20-layer configurations.
2. U-Net: Applied to CIFAR-10 and SVHN datasets, demonstrating adaptability to various image scales and complexities.

   Figure 2: Architecture of 10 layers and 20 layers fully connected autoencoders for the Tiny ImageNet dataset (a subset of images, at $64 \times 64 \times 3$ pixel size).

Experimental Results

Recovery Performance

The method shows a significant advantage in recovery performance, particularly in scenarios with unknown degradation masks. It achieves high recovery rates even under challenging conditions previously deemed impractical. Figure 3 illustrates that the proposed approach significantly outperforms both autoencoder iterations and generic inpainting techniques, especially in accurate recovery scenarios.

Figure 3: Accurate recovery rates for recovery from degradation due to various missing pixel masks, tested on different architectures.

Noise Robustness

The evaluation also considers additive noise, with results indicating robust recovery capabilities under moderate noise levels. This robustness emphasizes the method's potential in real-world applications, where imaging conditions can often introduce noise.

Figure 4: Recovery results of degraded samples with additive noise.

Conclusion

The paper provides a novel perspective on evaluating memorization in autoencoders by framing it as an inverse problem. The proposed methodological framework significantly enhances recovery rates of training data, thereby offering a more detailed empirical evaluation of memorization phenomena. This approach highlights the potential for further research into the intersection of inverse problems and deep learning, particularly concerning overparameterization and data memorization. Future work may explore extensions to other forms of neural networks and applications beyond image recovery.