Robust PCA for Anomaly Detection and Data Imputation in Seasonal Time Series (2208.01998v1)

Abstract: We propose a robust principal component analysis (RPCA) framework to recover low-rank and sparse matrices from temporal observations. We develop an online version of the batch temporal algorithm in order to process larger datasets or streaming data. We empirically compare the proposed approaches with different RPCA frameworks and show their effectiveness in practical situations.

• The paper introduces an online RPCA method that decomposes seasonal time series into low-rank, sparse, and noise components for effective anomaly detection and data imputation.
• It employs temporal regularization terms and a moving window approach to adaptively handle non-stationary data and improve reconstruction quality.
• Experimental results show that the framework outperforms traditional batch RPCA in real-world scenarios while maintaining competitive performance on synthetic data.

Robust PCA for Time Series Analysis

This paper (2208.01998) introduces a framework employing Robust Principal Component Analysis (RPCA) for anomaly detection and data imputation in seasonal time series. It presents an online version of a batch temporal algorithm to handle large datasets and streaming data, comparing its performance against existing RPCA methods. The key idea is to decompose a time series into low-rank, sparse, and noise components, which allows for the extraction of smooth signals and the identification of anomalies.

Problem Formulation and RPCA Variants

The paper addresses the challenge of analyzing corrupted time series data, where corruptions include missing data, anomalies, and noise. The time series $\mathbf{y}$ is transformed into a matrix $\mathbf{D} \in \mathbb{R}^{T_0 \times n}$, where $T_0$ is the main seasonality and $n$ is the number of periods. This matrix is then decomposed as $\mathbf{D} = \mathbf{X} + \mathbf{A} + \mathbf{E}$, where $\mathbf{X}$ is a low-rank matrix, $\mathbf{A}$ is a sparse anomaly matrix, and $\mathbf{E}$ represents Gaussian noise. The goal is to estimate $\mathbf{X}$ and $\mathbf{A}$ given the observed data $\mathbf{D}$.

The standard RPCA formulation minimizes the following objective function:

$\min_{\substack{ \mathbf{X}, \mathbf{\tilde{A} \ \text{ s.t. } \mathcal{P}_{\Omega} (\mathbf{D}) = \mathcal{P}_{\Omega} (\mathbf{X} + \mathbf{\tilde{A}) } \Vert \mathbf{X} \Vert_* + \lambda_2 \Vert \mathbf{\tilde{A} \Vert_1,$

where $\Omega$ is the set of observed data, $\mathcal{P}_{\Omega}$ is the projection operator onto $\Omega$, $\Vert \cdot \Vert_*$ is the nuclear norm, and $\Vert \cdot \Vert_1$ is the $\ell_1$-norm. $\lambda_2$ is a regularization parameter. The paper argues that this formulation does not explicitly account for temporal dependencies present in time series data.

To address this limitation, the authors introduce temporal regularization terms that penalize differences between columns spaced by specific time lags $T_k$. This leads to the following objective function:

$$\min_{\mathbf{X}, \mathbf{A}} \frac{1}{2} \Vert \mathcal{P}_{\Omega}(\mathbf{D} - \mathbf{X} -\mathbf{A}) \Vert_F^2 + \lambda_1 \Vert \mathbf{X} \Vert_* + \lambda_2 \Vert \mathbf{A} \Vert_1 + \sum_{k=1}^K \eta_k \Vert \mathbf{XH_k} \Vert_F^2$$

where $\Vert \cdot \Vert_F$ is the Frobenius norm, $\mathbf{H_k}$ are Toeplitz matrices encoding the temporal dependencies, and $\eta_k$ are regularization parameters. This formulation can be interpreted as RPCA on a graph, where the $\mathbf{H_k}$ matrices define the neighborhood structure.

Online RPCA Algorithm

The paper also presents an online version of the RPCA algorithm with temporal regularization to address the limitations of batch algorithms, which require storing all data in memory and are not suitable for streaming data. The online algorithm is based on stochastic optimization, where the low-rank matrix $\mathbf{X}$ is represented as a product of two matrices, $\mathbf{L}$ and $\mathbf{Q}$, i.e., $\mathbf{X} = \mathbf{LQ}^\top$. The algorithm iteratively updates $\mathbf{L}$, $\mathbf{Q}$, and $\mathbf{A}$ using stochastic gradient descent.

To handle non-stationary time series, the authors introduce a moving window approach, where the basis $\mathbf{L}$ is updated using only the most recent $n_w$ samples. This allows the algorithm to adapt to changes in the underlying subspace over time.

Experimental Results

The proposed framework is evaluated on both synthetic and real-world time series data. The synthetic data consists of corrupted sine functions, while the real-world data is Automatic Ticket Counting data representing train ticketing validations. The performance of the algorithms is measured in terms of reconstruction error, F1-score, and precision score for anomaly detection.

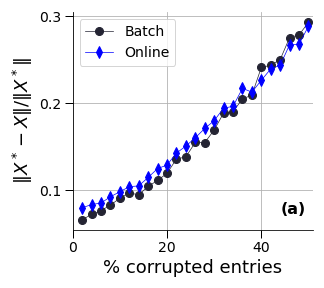
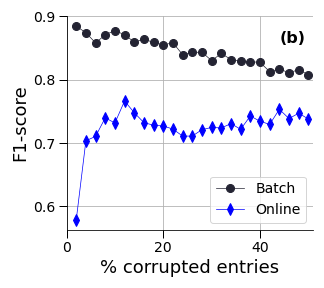
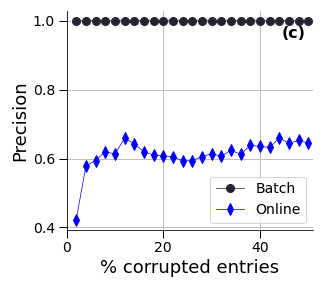
Figure 1: Comparison of two RPCA formulations: batch or online with additional temporal regularisations. (a) reconstruction errors; (b) F1-scores for the anomaly detection and (c) precision scores for the anomaly detection--with respect to the percentage of corrupted data.

The results on synthetic data (Figure 1) show that the batch and online versions achieve similar reconstruction quality, while the batch version outperforms the online version in terms of anomaly detection. However, on the real-world dataset, the online versions, especially the online RPCA with a moving window, perform better than the batch versions. The authors attribute this to the non-stationary nature of the real-world data, where the moving window approach allows the algorithm to adapt to changes in the underlying subspace.

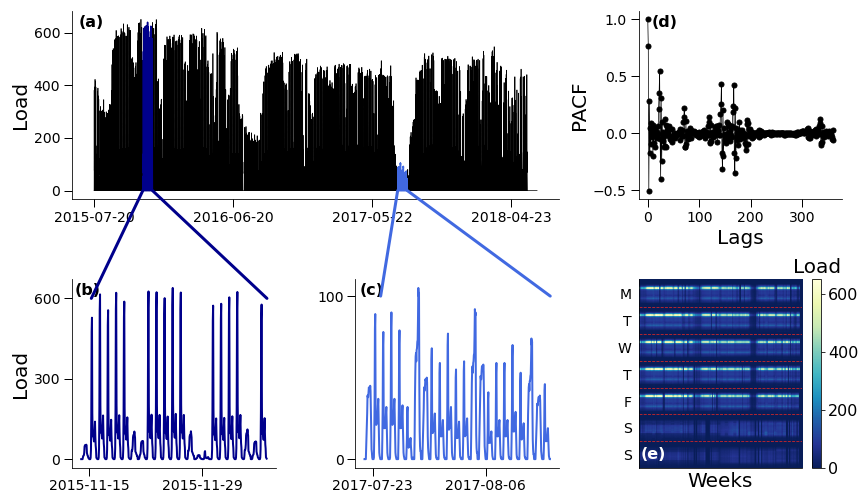
Figure 2: RPCA on a validation profile. (a) Entire time series of ticketing validations at the Athis-Mons station. (b) and (c) Focus on a subpart of the time series. (d) The time series displays a strong weekly seasonality, and to a lesser extent, a daily seasonality. (e) Matrix $\mathbf{D}$ associated to the time series in (a).

Figure 3: Comparison of four RPCA formulations on a validation profile: batch or online and with or without additional temporal regularisations ($T_1=1$, i.e. similarity between consecutive weeks) (a) reconstruction errors and (b) precision scores for the anomaly detection; with respect to the percentage of corrupted data. The online versions offer the best reconstructions whilst the temporal ones are better at avoiding false positives. (c) RPCA filtering on modal decompositions: focus on the first modes computed on the resulting low-rank matrices.

The paper also investigates the impact of RPCA filtering on modal decompositions, showing that applying RPCA before calculating the decomposition leads to smaller differences between the first modes of the original and corrupted data (Figure 3). This demonstrates the effectiveness of RPCA in recovering coherent structures.

Conclusion

The paper presents a comprehensive framework for anomaly detection and data imputation in seasonal time series using RPCA. The introduction of temporal regularization terms and an online algorithm with a moving window are significant contributions. The experimental results demonstrate the effectiveness of the proposed methods on both synthetic and real-world data. The method is fully adaptive and requires little knowledge of the dataset. A cross-validation strategy is also used for hyperparameter tuning.