SymForce: Symbolic Computation and Code Generation for Robotics (2204.07889v2)

Abstract: We present SymForce, a library for fast symbolic computation, code generation, and nonlinear optimization for robotics applications like computer vision, motion planning, and controls. SymForce combines the development speed and flexibility of symbolic math with the performance of autogenerated, highly optimized code in C++ or any target runtime language. SymForce provides geometry and camera types, Lie group operations, and branchless singularity handling for creating and analyzing complex symbolic expressions in Python, built on top of SymPy. Generated functions can be integrated as factors into our tangent-space nonlinear optimizer, which is highly optimized for real-time production use. We introduce novel methods to automatically compute tangent-space Jacobians, eliminating the need for bug-prone handwritten derivatives. This workflow enables faster runtime code, faster development time, and fewer lines of handwritten code versus the state-of-the-art. Our experiments demonstrate that our approach can yield order of magnitude speedups on computational tasks core to robotics. Code is available at https://github.com/symforce-org/symforce.

• The paper presents a novel library that bridges symbolic computation in Python and optimized C++ code generation to accelerate real-time robotics performance.
• It employs algebraic simplification, common subexpression elimination, and sparsity exploitation to achieve order-of-magnitude speedups over traditional methods.
• The approach integrates a tailored optimization framework with tangent-space differentiation and branching-free singularity handling for robust performance.

Symbolic Computation and Code Generation for Robotics

SymForce is presented as a symbolic computation and code generation library designed to bridge the gap between the flexibility of symbolic mathematics in Python and the performance of optimized code in C++ for robotics applications (2204.07889). It enables developers to define problems symbolically, experiment with them, and generate optimized code that can be used in real-time optimization scenarios.

Core Components and Architecture

SymForce's architecture, as illustrated in (Figure 1), comprises three primary components: symbolic computation, code generation, and optimization.

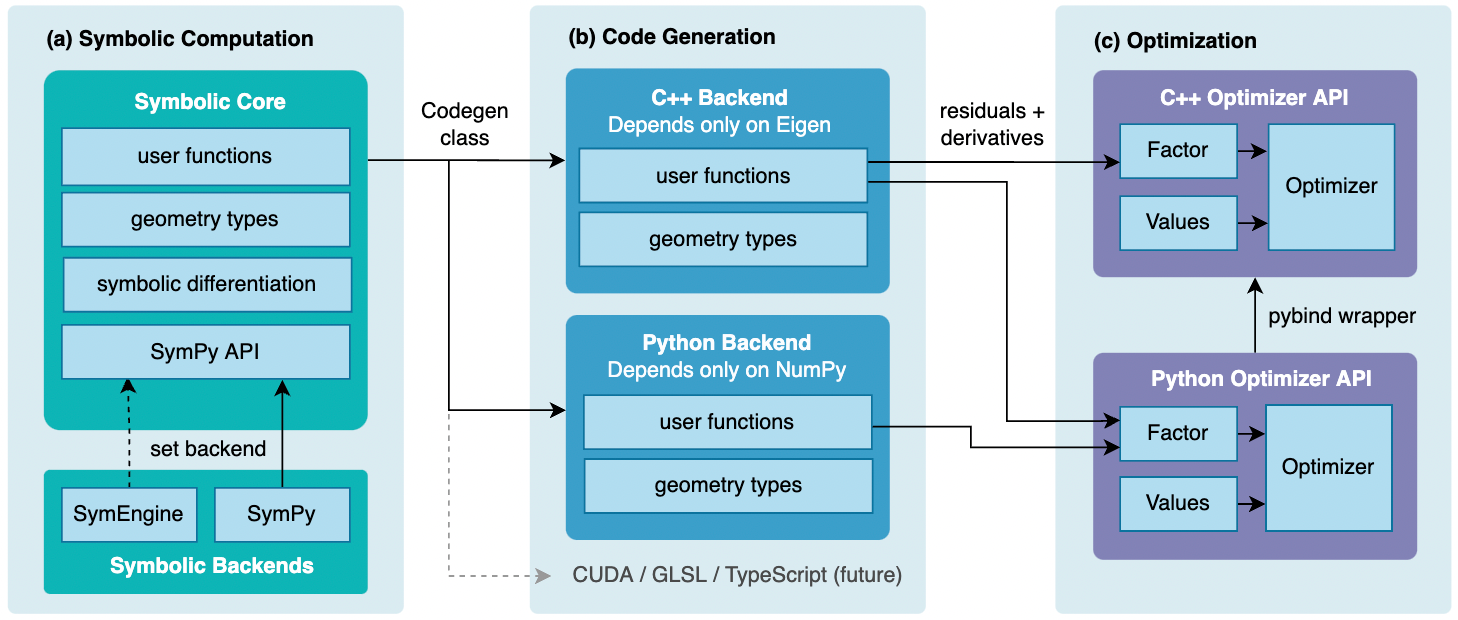
Figure 1: SymForce architecture diagram, outlining the workflow from symbolic expression in Python to autogenerated, optimized C++ code used in a nonlinear optimizer.

Symbolic Computation

At its core, SymForce extends the SymPy API, providing tools for building and analyzing symbolic expressions in Python. This allows for algebraic manipulation of mathematical expressions, facilitating tasks such as substitution, simplification, differentiation, and solving. The library supports both SymPy and SymEngine as symbolic backends, with SymEngine offering faster performance for manipulating large expressions. SymForce also includes symbolic implementations of common robotics types like matrices, rotations, poses, and camera models. These types are defined as Python classes, and fast runtime classes with identical interfaces are autogenerated for target languages like C++. To ensure generic code can operate on all geometry types, SymForce employs a concepts mechanism inspired by GTSAM. This mechanism defines three primary concepts: StorageOps, GroupOps, and LieGroupOps, which enable types to be converted to and from sequences of scalars, registered as mathematical groups, and registered as Lie groups, respectively.

Code Generation

The code generation process in SymForce is facilitated by the Codegen class, which leverages SymPy's code printers and adds support for struct types, Eigen/NumPy matrices, and geometry types. A key step in this process is CSE, which identifies duplicate intermediate terms within a symbolic expression and pulls them out into temporary variables. This results in significant efficiency gains. The paper provides an example of a symbolic function that computes the residual of the position of a point expressed in a local frame to a point expressed in the world frame. The Codegen.function method generates native code for this function, demonstrating the library's ability to produce human-readable and efficient code.

Optimization Framework

SymForce's optimization library, available in both C++ and Python, is designed to work with the code generation tools and Lie group types. It performs tangent space optimization using a factor graph formulation inspired by GTSAM and implements a low-overhead version of the Levenberg-Marquardt algorithm. As an example, the point_residual function can be interpreted as a residual between two points, parameterized by the pose world_T_local. To minimize this residual, a function is generated that computes the Jacobian $J$ of the residual $b$, as well as the Gauss-Newton approximation for the Hessian $J^T J$ and right-hand side $J^T b$. This function is generated automatically from point_residual using Codegen.with_linearization. The library also provides a GncOptimizer subclass of Optimizer that implements GNC, a method for transitioning from a convex cost function to a robust cost function as the optimization converges.

Speed Advantages

The paper highlights three primary ways in which symbolic computation speeds up code execution: function flattening, sparsity exploitation, and algebraic simplification.

Function Flattening

SymForce generates runtime functions that consist of a single chain of instructions that share all common subexpressions. This process of flattening improves cache performance.

Sparsity Exploitation

SymForce leverages sparsity in matrix multiplication by symbolically multiplying matrices and generating code for the result. This significantly reduces the number of operations required.

Algebraic Simplification

SymForce employs algebraic simplification to transform symbolic expressions into forms that are faster to compute. This includes techniques such as expansion, factorization, term collection, and trigonometric identities.

The combination of these three strategies results in substantial performance improvements, particularly in scenarios involving complex expressions and sparse matrices.

Symbolic Differentiation and Singularity Handling

Tangent-Space Differentiation on Lie Groups

The paper introduces two novel methods for automatically computing tangent-space derivatives of Lie group elements: symbolic application of the chain rule and first-order retraction. The first-order retraction method typically outperforms the symbolic chain rule method and is the default approach for computing tangent-space Jacobians in SymForce.

Branching and Singularity Handling

To avoid branches in algorithmic functions, particularly in the context of handling singularity points, the paper suggests using primitives like the sign function, absolute value, floor, min, and max. The library also introduces a novel method for handling removable singularities within symbolic expressions by shifting the input to the function away from the singular point with an infinitesimal variable $\epsilon$. This approach avoids the need for branching and minimizes performance impact.

Experimental Validation

The paper presents benchmark results on a variety of problems, including matrix multiplication, inverse compose, and robot 3D localization. These experiments demonstrate that SymForce can achieve order-of-magnitude speedups compared to alternative approaches, such as Eigen, GTSAM, Sophus, Ceres, and JAX. The matrix multiplication experiments show that SymForce's flattened functions outperform dense and sparse matrix multiplication using Eigen. The inverse compose experiment demonstrates that SymForce's flattened expressions are significantly faster than automatic differentiation approaches. The robot 3D localization example highlights the performance gains that can be achieved by flattening the entire linearization into a single function that shares all computation. (Figure 2) shows that SymForce outperforms sparse and dense matrix multiplication with Eigen.

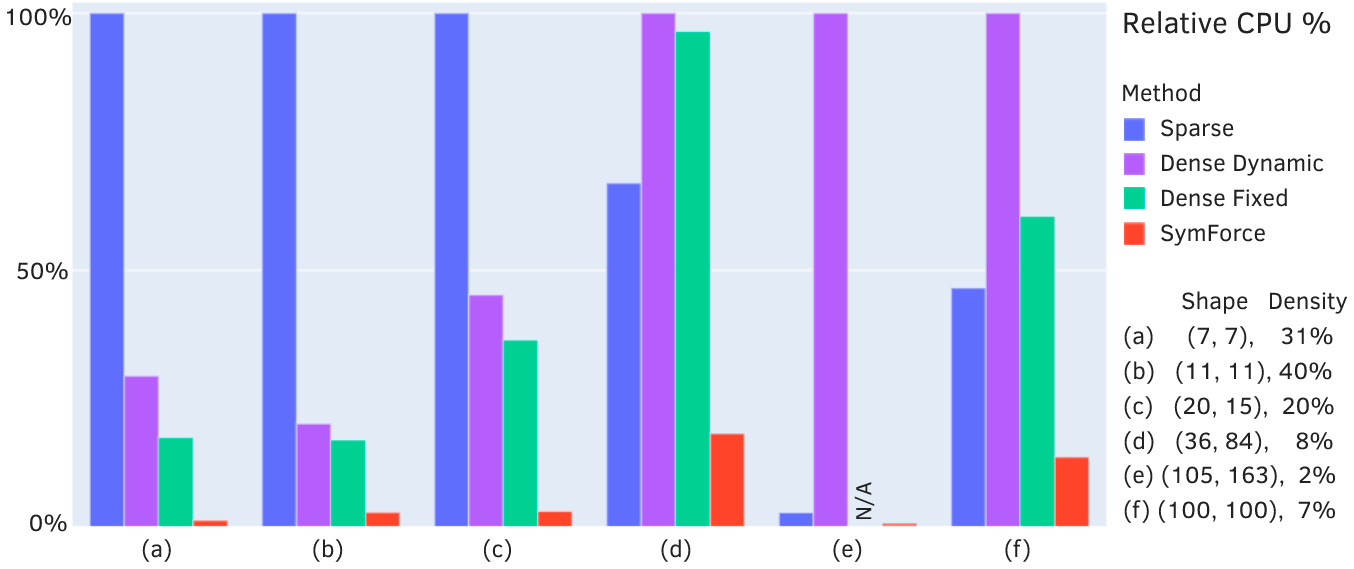
Figure 2: SymForce outperforms sparse and dense matrix multiplication with the Eigen library, sharing common subexpressions and leveraging sparsity with no runtime overhead.

Limitations

The paper identifies several limitations of SymForce. The separation between symbolic and runtime contexts requires a higher level of abstraction, which can be challenging for some users. The method of flattening expressions can become impractical with highly nested expressions, leading to long compile times and poor cache performance. Some symbolic routines, like simplification and factorization, can be slow with large expressions. Finally, SymForce is most suitable for generating functions with up to hundreds of input variables and hundreds of thousands of instructions.

Conclusion

SymForce is presented as a powerful tool for symbolic computation and code generation, particularly for real-time robotics applications. It enables faster runtime code, reduces development time, and requires fewer lines of handwritten code compared to state-of-the-art alternatives. Its performance advantages stem from autogenerating code that flattens across function calls and matrix multiplications, taking advantage of common subexpressions and problem sparsity.