Measuring Mathematical Problem Solving With the MATH Dataset (2103.03874v2)

Abstract: Many intellectual endeavors require mathematical problem solving, but this skill remains beyond the capabilities of computers. To measure this ability in machine learning models, we introduce MATH, a new dataset of 12,500 challenging competition mathematics problems. Each problem in MATH has a full step-by-step solution which can be used to teach models to generate answer derivations and explanations. To facilitate future research and increase accuracy on MATH, we also contribute a large auxiliary pretraining dataset which helps teach models the fundamentals of mathematics. Even though we are able to increase accuracy on MATH, our results show that accuracy remains relatively low, even with enormous Transformer models. Moreover, we find that simply increasing budgets and model parameter counts will be impractical for achieving strong mathematical reasoning if scaling trends continue. While scaling Transformers is automatically solving most other text-based tasks, scaling is not currently solving MATH. To have more traction on mathematical problem solving we will likely need new algorithmic advancements from the broader research community.

• The paper introduces the MATH dataset with 12,500 high school competition problems and detailed step-by-step solutions to measure machine mathematical reasoning.
• It uses exact match scoring to assess GPT-based models, revealing modest performance improvements despite increased model scale.
• The study highlights that integrating partial ground truth solutions enhances logical reasoning, underscoring the need for innovative algorithmic approaches.

Measuring Mathematical Problem Solving With the MATH Dataset

Introduction

The paper "Measuring Mathematical Problem Solving With the MATH Dataset" (2103.03874) provides a comprehensive framework to evaluate mathematical reasoning abilities in machine learning models. This effort aims to bridge the gap in machine numeric capabilities by introducing the MATH dataset, containing $12,500$ competition-style problems, classified by difficulty and subject. The paper proposes that solving such complex mathematical problems requires more than scaled computational resources, emphasizing the need for algorithmic innovations.

MATH Dataset Overview

The MATH dataset comprises high school competition problems, structured to test comprehensive mathematical reasoning across various subjects and difficulties. Problems are tagged by difficulty levels from $1$ (easiest) to $5$ (hardest), covering topics like algebra, geometry, and number theory. Each problem is accompanied by step-by-step solutions in LaTeX, enabling models to learn both final answer derivations and intermediate mathematical reasoning steps.

Figure 1: Problems, step-by-step solutions generated by our GPT-2 1.5B model, and ground truth solutions.

The uniqueness of this dataset lies in its scoring methodology; the answers are assessed using exact match scores, circumventing subjective metrics such as BLEU. This provides a robust mechanism to quantify the actual mathematical problem-solving capacity of models without heuristic biases.

Performance Metrics and Model Evaluation

The paper highlights that even with extensive resources, including auxiliary data for pretraining, the performance of advanced models remains modest. Models based on GPT architectures show sluggish accuracy growth in correlation with increased parameters—a stark contrast to other NLP tasks where larger models tend to achieve significantly better performance.

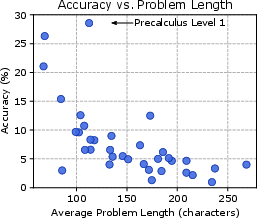
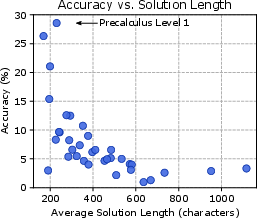
Figure 2: Subject accuracy vs problem length.

Extensive evaluations reveal a negligible performance difference when models are scaled, indicating that existing state-of-the-art architectures might be inadequately equipped for tackling MATH’s complexity.

Auxiliary Mathematics Problems and Solutions (AMPS) Dataset

Complementing the MATH dataset, the paper introduces the AMPS pretraining dataset, comprising structured problems and solutions sourced from educational platforms like Khan Academy. This dataset aims to instill foundational mathematical concepts, enabling models to build upon these to tackle more challenging tasks in MATH.

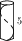
Figure 3: Example of asymptote code and the figure it produces.

Step-by-Step Solutions and Algorithmic Insights

A novel experiment conducted involved generating step-by-step solutions for given problems. Although GPT-2 demonstrated modest coherence in its generated solutions, it often failed to achieve the correct answer, indicating a deficiency in logical consistency and problem-solving timestamping.

Yet, the paper found that models significantly benefit from partial ground truth solutions during training, indicating that step-by-step learning improves the interpretability and decision-making capabilities of neural architectures.

Figure 4: Additional example problems, generated solutions, and ground truth solutions from our MATH dataset.

Conclusion

The introduction of the MATH dataset alongside AMPS presents a new frontier for quantitative machine reasoning tasks. Despite the incremental improvements from existing models, the research underscores the need for the AI community to develop innovative algorithmic solutions to truly harness machine learning for solving complex mathematical problems. Future avenues might involve integrating alternate computational paradigms or hybrid frameworks to cross the current limitations highlighted by the dataset analyses.

The implications for AI research are profound, offering not only an empirical basis for mathematical reasoning capabilities but also providing directions for the seminal work necessary to advance the domain of automated theorem proving and number theory in computational frameworks.