Krylov Complexity for Open Quantum System: Dissipation and Decoherence (2509.14810v1)

Abstract: We investigate Krylov complexity in open quantum systems using Lindblad master equations for bosonic bath models, with particular emphasis on the Caldeira--Leggett model. Krylov complexity is computed from the moments of the two-point function within the standard master equation framework. For the damped harmonic oscillator, the results reveal clear dissipative features in Krylov complexity. In the Caldeira--Leggett model, in the high-temperature limit, we find that Krylov complexity saturates in the full system and reproduces the expected dissipative behavior when the decoherence term is suppressed in the master equation. Conversely, when the dissipative term is suppressed, the contribution from decoherence exhibits the familiar oscillatory dynamics of the coherent system, along with additional novel features. However, Krylov complexity appears insensitive to the onset of decoherence, as no clear distinctive signature is observed. We attribute this to the fact that Krylov complexity is defined in the Krylov basis, which does not coincide with the conventional basis typically used to study decoherence.

• The paper demonstrates that Krylov complexity effectively captures dissipative dynamics, revealing clear saturation in damped harmonic oscillators.
• It employs the bi-Lanczos algorithm and moments method to quantify operator growth, simplifying analysis of high-dimensional systems.
• The study finds that Krylov complexity is relatively insensitive to decoherence, emphasizing basis choice in diagnosing quantum information dynamics.

Krylov Complexity in Open Quantum Systems: Dissipation and Decoherence

Introduction

This paper presents a systematic paper of Krylov complexity in open quantum systems, focusing on the interplay between dissipation and decoherence. The analysis is conducted using Lindblad master equations for bosonic bath models, with particular emphasis on the Caldeira–Leggett model. Krylov complexity, defined via the moments of the two-point function, is evaluated for both the damped harmonic oscillator and the Caldeira–Leggett system. The work aims to clarify whether Krylov complexity is sensitive to decoherence, as is known for circuit complexity, and to delineate its behavior under dissipative dynamics.

Krylov Complexity: Formalism and Computation

Krylov complexity quantifies operator growth in the Krylov subspace, constructed from nested commutators of the Liouvillian superoperator with a chosen operator. The evolution of the operator in this basis is governed by a Schrödinger-like equation parameterized by Lanczos coefficients, which encode the system's dynamical properties. For open quantum systems, the non-Hermitian nature of the Lindbladian necessitates the use of the bi-Lanczos algorithm, yielding a tridiagonal matrix with complex off-diagonal elements. A similarity transformation is employed to symmetrize these off-diagonals, facilitating the computation of moments and, consequently, Krylov complexity.

The moments method, based on derivatives of the autocorrelation function, provides a practical route to extract the Lanczos coefficients. This approach is particularly advantageous for high-dimensional systems, as it reduces the complexity of the problem to a one-dimensional chain.

Damped Harmonic Oscillator: Dissipative Dynamics

The damped harmonic oscillator serves as a prototypical example of dissipation in open quantum systems. The Lindblad master equation, with a single jump operator proportional to the annihilation operator, models photon emission into a zero-temperature bath. Krylov complexity is computed using the moments method, revealing rapid initial growth followed by decay to a low saturation value. This behavior is in stark contrast to the closed harmonic oscillator, where complexity exhibits periodic oscillations due to coherent evolution.

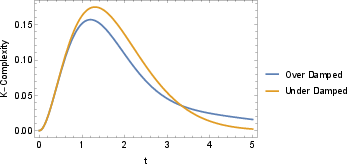
Figure 1: Time evolution of Krylov complexity (K-complexity) for under-damped ($\omega = 1$, $\gamma = 0.1$) and over-damped ($\omega = 1$, $\gamma = 0.9$) systems.

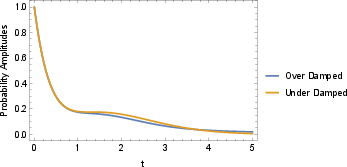
Figure 2: Time evolution of probability amplitudes for under-damped and over-damped systems, illustrating the slower decay in the underdamped regime.

The numerical results confirm that dissipation leads to reduced complexity and lower saturation values. In the overdamped regime, the operator explores only a limited portion of the system space before dissipating into the bath, while in the underdamped regime, a larger portion is explored prior to loss.

Caldeira–Leggett Model: Dissipation and Decoherence

The Caldeira–Leggett model describes a Brownian particle coupled to a thermal bath, with dynamics governed by a master equation containing distinct terms for dissipation and decoherence. The decoherence term, proportional to temperature, induces loss of phase coherence, while the dissipative term damps momentum expectation values.

The decoherence function, which tracks the decay of off-diagonal elements in the reduced density matrix, is evaluated and shown to saturate as the system reaches the maximum coherence length of the environment.

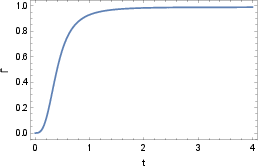
Figure 3: Time evolution of decoherence function $\Tilde{\Gamma}$ for $\omega = 1$ and $\gamma = 0.1$, demonstrating saturation at late times.

Krylov complexity in the Caldeira–Leggett model exhibits initial oscillatory behavior with secondary frequency modes ("anti-oscillations") and ultimately saturates at late times, reflecting the interplay between dissipation and decoherence.

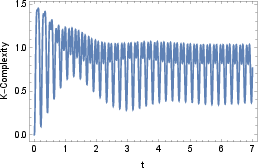
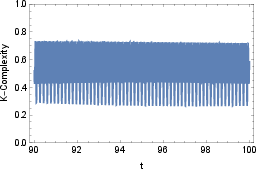
Figure 4: Time evolution of Krylov complexity for the Caldeira–Leggett master equation with $\omega = 1$ and $\gamma = 1/10$; right panel shows late-time saturation.

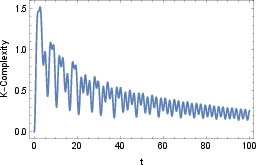
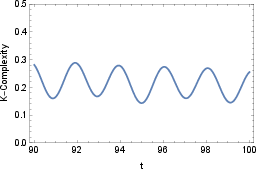
Figure 5: Krylov complexity for $\omega = 1/10$ and $\gamma = 1/20$, with clear saturation at late times.

The saturation value is significantly lower than in closed systems, and the timescale for saturation depends on the relative strengths of dissipation and decoherence.

Decomposition of Master Equation: Isolating Effects

To disentangle the contributions of dissipation and decoherence, the master equation is decomposed by selectively suppressing individual terms. When the dissipative term is turned off, Krylov complexity exhibits persistent oscillations without saturation, indicating that dissipation is responsible for the decay and eventual saturation.

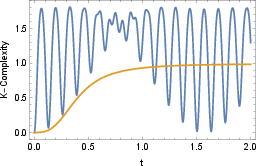
Figure 6: Left: Krylov complexity for $\omega = 1$, $\gamma = 1/100$ with dissipation suppressed. Right: Overlay of Krylov complexity and decoherence function, showing lack of clear correlation.

Conversely, suppressing the decoherence term by choosing an appropriate operator (e.g., $O = x^2$) recovers the dissipative behavior observed in the damped harmonic oscillator, with sharp initial growth and oscillatory decay.

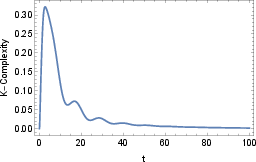
Figure 7: Krylov complexity and probability amplitudes for the Caldeira–Leggett master equation with $O = x^2$, $\omega = 1$, and $\gamma = 1/10$.

Comparison with Circuit Complexity and Basis Dependence

A key finding is that Krylov complexity does not exhibit clear signatures of the onset of decoherence, in contrast to circuit complexity, which is sensitive to the transition to mixedness. This insensitivity is attributed to the choice of basis: the Krylov basis does not coincide with the preferred basis for studying decoherence, where off-diagonal elements of the density matrix decay. As a result, Krylov complexity primarily reflects operator growth and dissipation, rather than the decay of system–bath correlations.

Implications and Future Directions

The results demonstrate that Krylov complexity is a robust probe of dissipative dynamics in open quantum systems, with clear numerical signatures of saturation and reduced complexity. However, its utility as a diagnostic for decoherence is limited by basis dependence. This suggests that future work should explore operator growth in the preferred basis to enhance sensitivity to decoherence phenomena.

Extensions to curved-space models and the paper of recoherence are promising avenues for further research. Additionally, the interplay between Krylov and circuit complexity in various open system models warrants deeper investigation, particularly in the context of quantum information processing and quantum thermodynamics.

Conclusion

This paper provides a comprehensive analysis of Krylov complexity in open quantum systems, elucidating its behavior under dissipation and decoherence. Krylov complexity effectively captures dissipative effects, with clear numerical signatures of saturation and reduced operator growth. However, it is relatively insensitive to the onset of decoherence, highlighting the importance of basis choice in complexity diagnostics. The findings have significant implications for the paper of quantum information dynamics, operator growth, and the characterization of open quantum systems. Future work should focus on refining the basis for complexity measures and exploring their applications in more general settings.