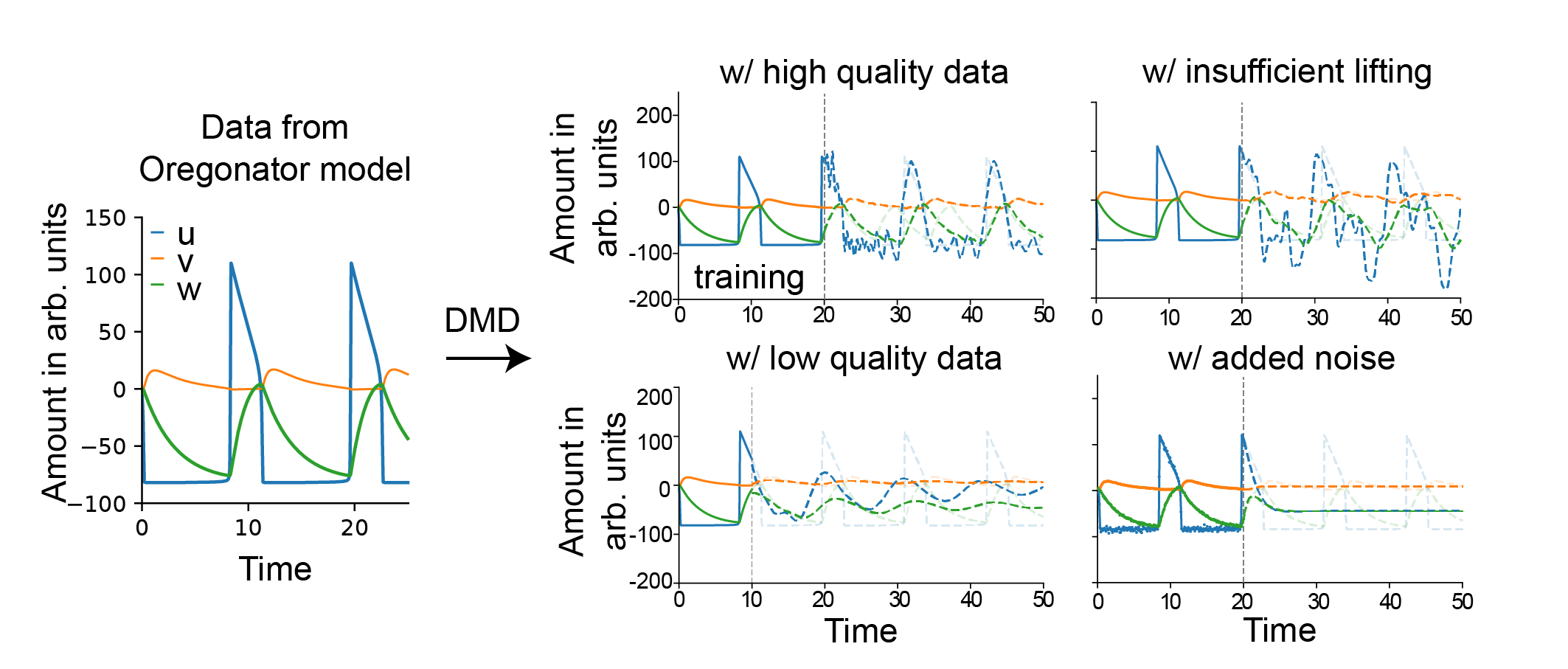Data-driven discovery of dynamical models in biology (2509.06735v1)

Abstract: Dynamical systems theory describes how interacting quantities change over time and space, from molecular oscillators to large-scale biological patterns. Such systems often involve nonlinear feedbacks, delays, and interactions across scales. Classical modeling derives explicit governing equations, often systems of differential equations, by combining mechanistic assumptions, experimental observations, and known physical laws. The growing complexity of biological processes has, however, motivated complementary data-driven methods that aim to infer model structure directly from measurements, often without specifying equations a priori. In this review, we survey approaches for model discovery in biological dynamical systems, focusing on three methodological families: regression-based methods, network-based architectures, and decomposition techniques. We compare their ability to address three core goals: forecasting future states, identifying interactions, and characterizing system states. Representative methods are applied to a common benchmark, the Oregonator model, a minimal nonlinear oscillator that captures shared design principles of chemical and biological systems. By highlighting strengths, limitations, and interpretability, we aim to guide researchers in selecting tools for analyzing complex, nonlinear, and high-dimensional dynamics in the life sciences.

• The paper demonstrates that regression-based methods can accurately recover governing equations under ideal conditions but are sensitive to noise and incomplete data.
• It benchmarks neural network methods, highlighting their flexibility in modeling complex dynamics while noting challenges in interpretability and generalization.
• The review emphasizes hybrid approaches leveraging Koopman theory to balance interpretability with predictive power in data-driven biological modeling.

Data-Driven Discovery of Dynamical Models in Biology

Introduction and Motivation

The paper "Data-driven discovery of dynamical models in biology" (2509.06735) provides a comprehensive review and critical assessment of methodologies for inferring dynamical models directly from biological time series data. The authors focus on the challenge of extracting mechanistic or predictive models from complex, nonlinear, and often high-dimensional biological systems, where classical approaches based on first-principles modeling are increasingly infeasible. The review is structured around three methodological families: regression-based methods, network-based (neural) architectures, and decomposition techniques, all unified under the operator-theoretic perspective of Koopman theory. The paper systematically benchmarks these approaches using the Oregonator model, a canonical nonlinear oscillator from chemical kinetics, and discusses their strengths, limitations, and interpretability in the context of biological data.

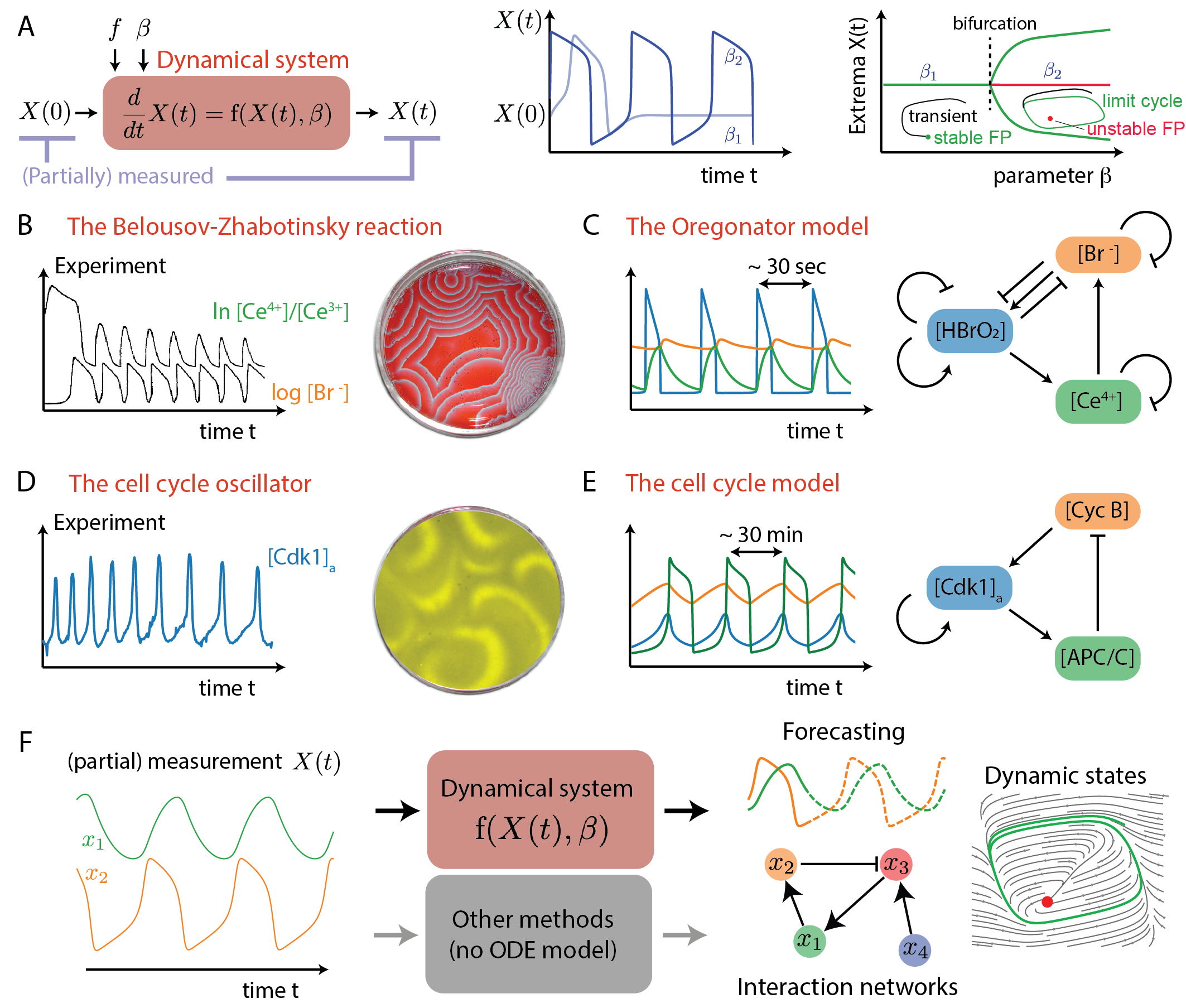
Figure 1: From data to dynamical systems in chemistry and biology, illustrating the transition from raw measurements to mechanistic or data-driven models, with examples from chemical and biological oscillators.

Theoretical Framework: Koopman Operator and Methodological Taxonomy

The review adopts Koopman operator theory as a unifying mathematical framework. In this perspective, nonlinear dynamical systems can be represented as linear (but infinite-dimensional) operators acting on observables, and the central challenge is to discover suitable finite-dimensional approximations or embeddings from data. This operator-theoretic view clarifies the relationships and trade-offs between different data-driven approaches:

• Regression-based methods seek explicit, often symbolic, representations of the governing equations or interaction networks, typically via sparse regression or symbolic regression.
• Network-based methods (e.g., neural networks) act as universal function approximators, learning nonlinear mappings or latent representations directly from data, but often at the expense of interpretability.
• Decomposition methods (e.g., Dynamic Mode Decomposition, DMD) extract dominant spatiotemporal modes and approximate the Koopman operator in a data-driven manner, providing low-dimensional linear representations of the dynamics.

This taxonomy is motivated by methodological constraints rather than philosophical distinctions (e.g., "white-box" vs. "black-box"), emphasizing the practical implications for forecasting, interaction inference, and state identification.

Regression-Based Approaches: Capabilities and Limitations

Regression-based methods are grouped into three main classes: causality inference, polynomial regression, and evolutionary (symbolic) regression.

• Causality methods (e.g., Granger causality, GOBI) infer directed interactions from time series but are limited in nonlinear or oscillatory regimes, often producing spurious results in synchronously coupled systems.
• Polynomial methods (e.g., NARMAX, SINDy) reconstruct explicit dynamical equations by fitting sparse polynomial expansions to the data. SINDy, in particular, is highlighted for its ability to recover the exact governing equations under ideal conditions (full observability, low noise, rich library), but its performance degrades rapidly with noise, partial observability, or incomplete basis functions.

  Figure 3: SINDy applied to Oregonator data demonstrates exact recovery of the model under ideal conditions, but fails with noise, partial observability, or incomplete libraries.

• Evolutionary methods (e.g., Symbolic Regression, AI-Feynman) search for both structure and parameters of candidate models using genetic programming or physics-inspired constraints. These methods are flexible and can rediscover known laws, but are computationally intensive and prone to overfitting without strong priors.

The review emphasizes that regression-based methods provide interpretable models but are highly sensitive to data quality, require full state observability, and do not scale well to high-dimensional systems. The Oregonator benchmark demonstrates that even moderate noise or missing variables can render these methods ineffective.

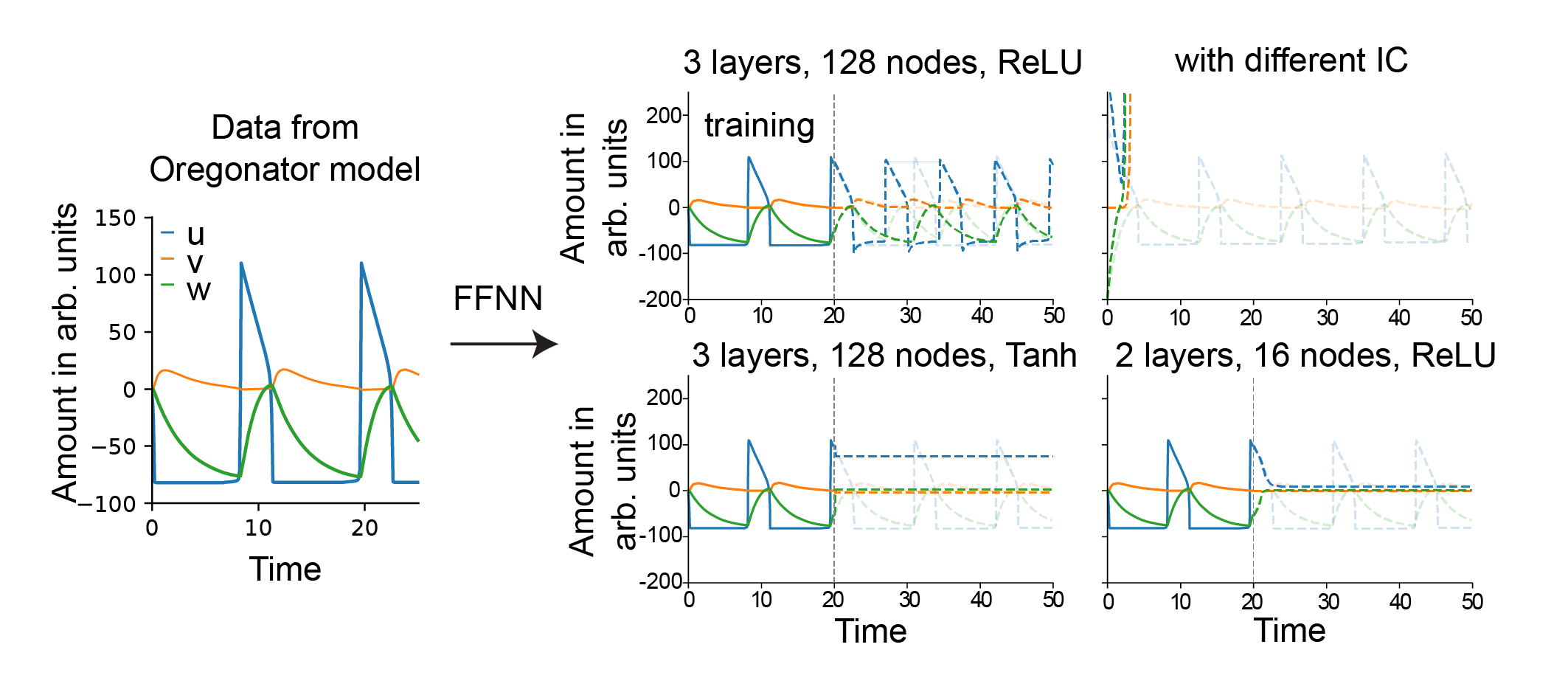
Network-Based Methods: Expressivity and Generalization

Neural network-based approaches, including feed-forward neural networks (FFNNs), recurrent neural networks (RNNs), and autoencoders (AEs), are discussed as flexible, high-capacity function approximators for dynamical systems.

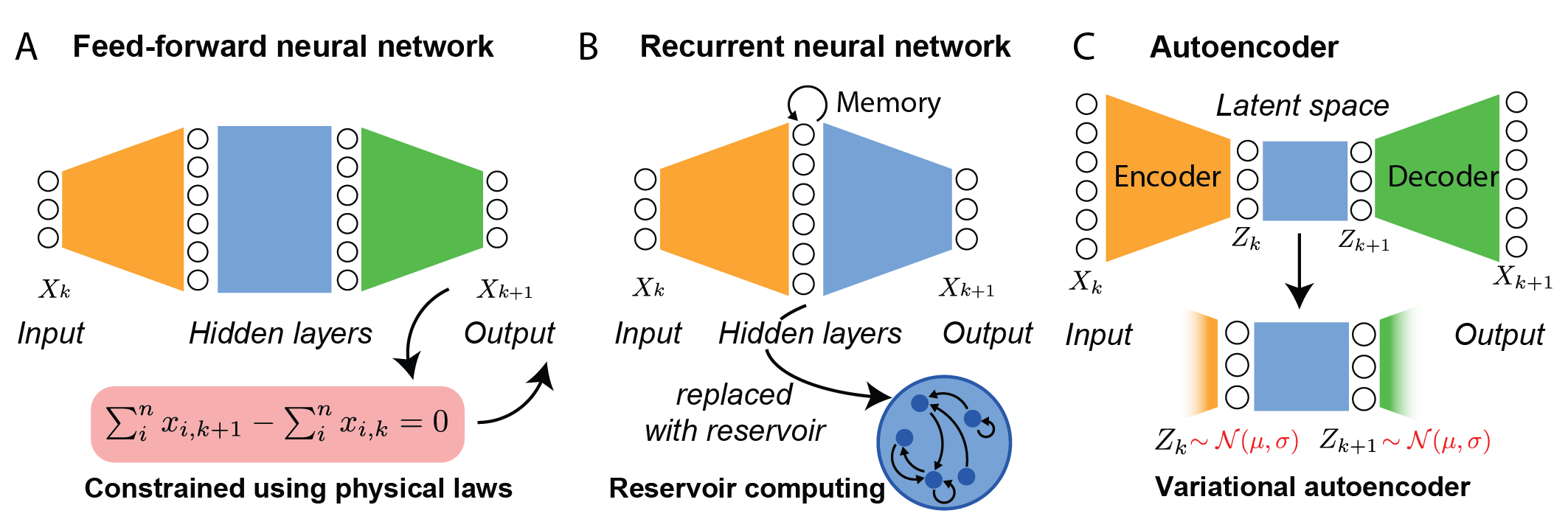
Figure 5: Schematic overview of neural network architectures for dynamical systems, including FFNNs, RNNs, and AEs, and their connections to physical or biological constraints.

• FFNNs can learn state-to-state mappings and are capable of reproducing complex dynamics within the training domain. However, they exhibit poor generalization to unseen initial conditions and are sensitive to architectural choices and data coverage.

  Figure 2: FFNNs trained on Oregonator data reproduce oscillatory dynamics within the training domain but fail to generalize to new initial conditions or with suboptimal architectures.

• RNNs and reservoir computing architectures incorporate memory and are well-suited for temporal data, but their interpretability is limited and they require large datasets for robust training.
• Autoencoders and variational autoencoders (VAEs) provide nonlinear dimensionality reduction and can learn latent representations that approximate Koopman-invariant coordinates, facilitating model reduction and analysis of high-dimensional data.

The main limitations of network-based methods are their lack of interpretability, dependence on hyperparameter tuning, and limited extrapolation beyond the training regime. Domain-informed variants (e.g., PINNs, BINNs) and hybrid approaches are proposed to mitigate these issues.

Decomposition Methods: Koopman-Based Linearization

Decomposition techniques, particularly DMD and its extensions (eDMD), are presented as direct data-driven approximations of the Koopman operator. These methods extract dominant spatiotemporal modes and provide linear representations of nonlinear dynamics in lifted feature spaces.

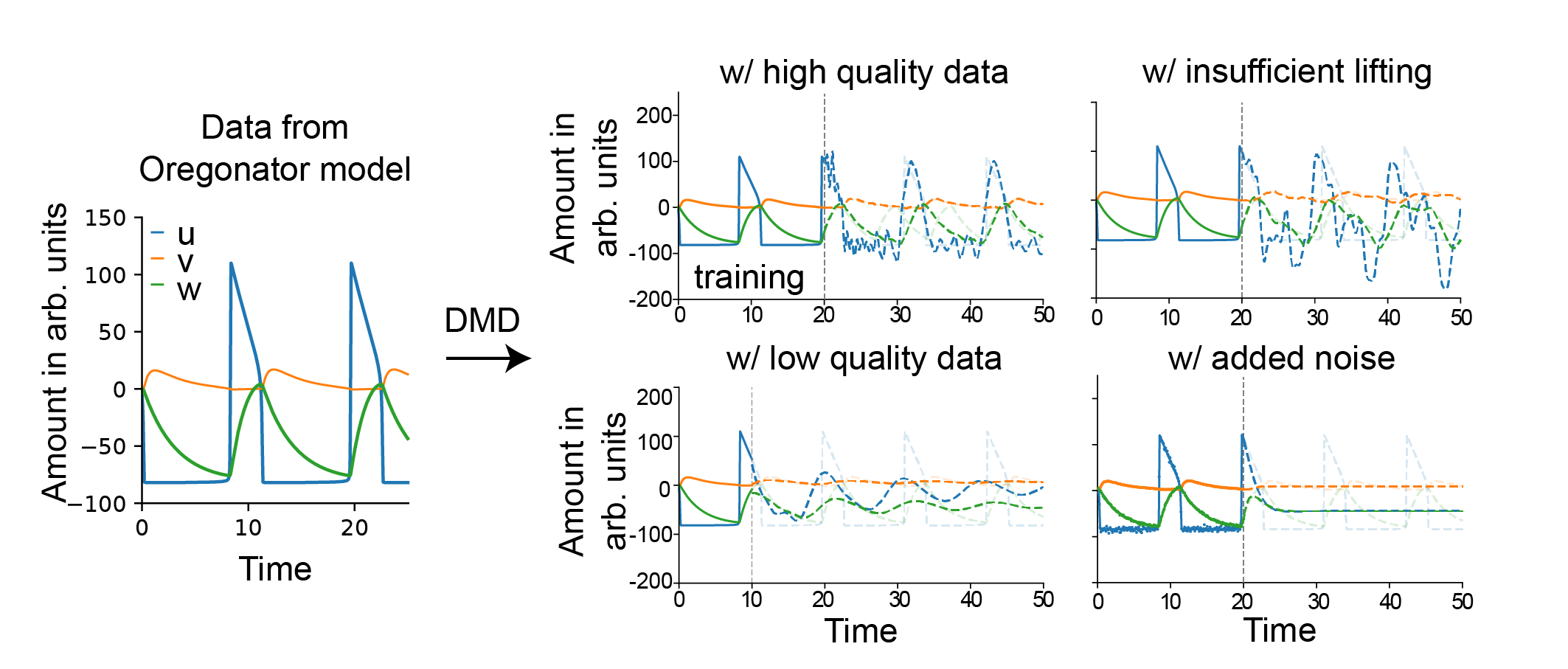
Figure 8: eDMD applied to Oregonator data captures oscillatory dynamics under ideal conditions with sufficient lifting, but fails with insufficient basis functions, low-quality data, or noise.

The review demonstrates that eDMD can accurately reproduce the qualitative behavior of the Oregonator model when provided with high-resolution, noise-free data and a sufficiently rich set of lifting functions. However, its performance deteriorates with limited data, noise, or inadequate feature selection, mirroring the challenges faced by regression-based methods.

Hybrid and Emerging Approaches

A major theme of the review is the emergence of hybrid methods that combine the strengths of regression-based and network-based approaches. Examples include:

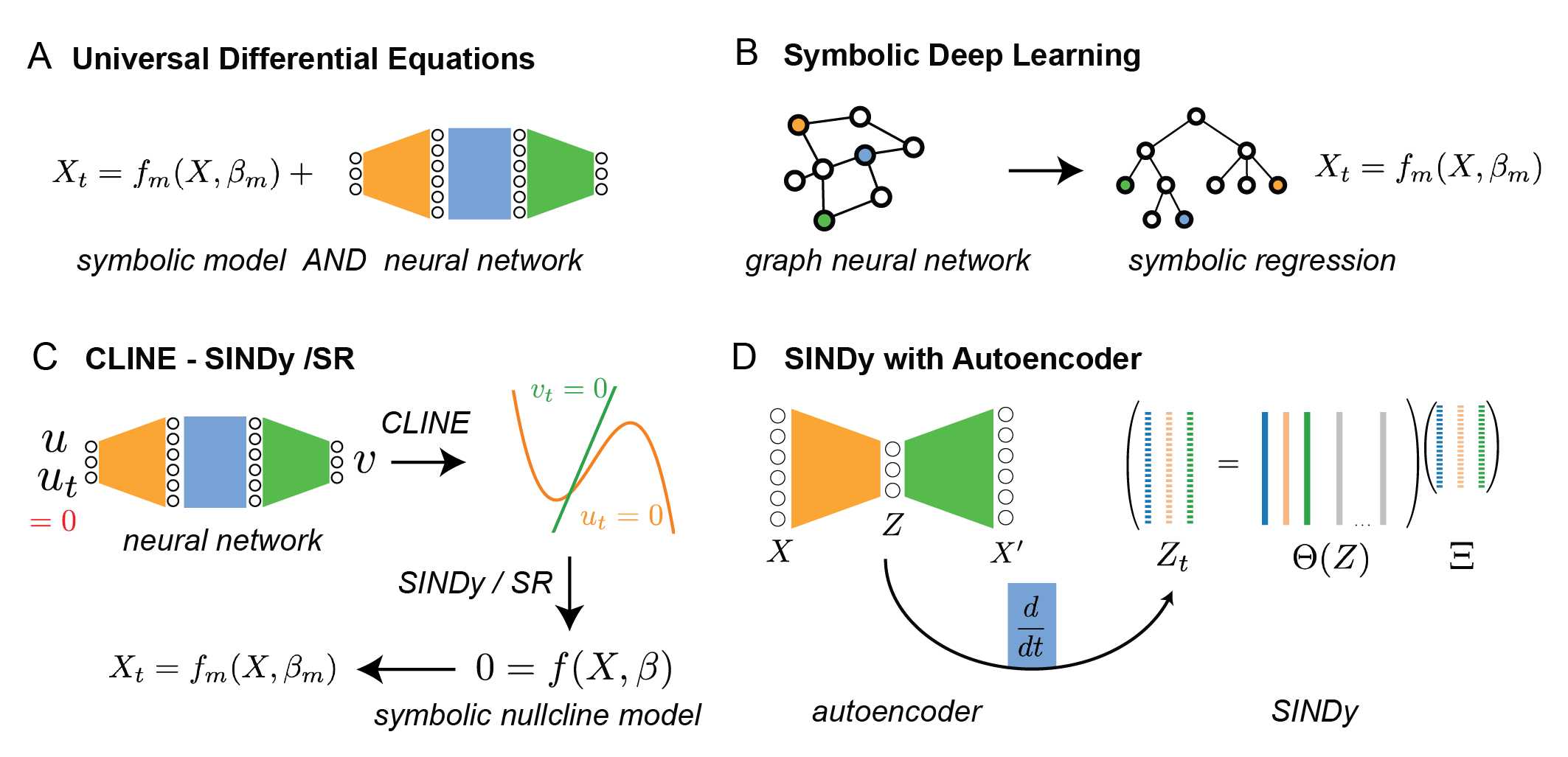
Figure 4: Hybrid methods integrate regression and network-based methodologies, such as UDEs, SDL, CLINE-SINDy/SR, and SINDy with autoencoders, to balance interpretability and flexibility.

• Universal Differential Equations (UDEs): Embed neural networks within mechanistic ODEs, allowing known components to be modeled explicitly and unknown components to be learned from data.
• Symbolic Deep Learning (SDL): Translate trained neural networks into symbolic expressions via symbolic regression, enhancing interpretability.
• CLINE-SINDy/SR: Use neural networks to identify geometric phase-space features (e.g., nullclines), which are then converted into explicit equations via SINDy or symbolic regression.
• SINDy with Autoencoders: Combine autoencoder-based dimensionality reduction with sparse regression in the latent space, enabling interpretable modeling of high-dimensional systems.

These hybrid approaches are positioned as promising solutions for overcoming the limitations of pure regression or network-based methods, particularly in the context of noisy, high-dimensional, and partially observed biological data.

Implications, Practical Considerations, and Future Directions

The review highlights several key implications for the application of data-driven modeling in biology:

• Data Quality and Experimental Design: High temporal resolution, low noise, and full state observability are critical for successful model discovery. Advances in experimental techniques (e.g., live-cell imaging, multi-omics) are expanding the scope of feasible applications.
• Interpretability vs. Predictive Power: There is an inherent trade-off between the interpretability of symbolic models and the predictive power of flexible neural architectures. Hybrid methods offer a pathway to balance these objectives.
• Scalability and Generalization: Most current methods struggle with high-dimensional systems and generalization beyond the training domain. Dimensionality reduction, domain-informed priors, and operator-theoretic embeddings are active areas of research.
• Integration with Probabilistic and Bayesian Frameworks: While not the focus of this review, probabilistic modeling and uncertainty quantification remain essential for robust inference in biological systems.

The authors argue that the ultimate goal is to enable the automated or semi-automated discovery of mechanistically interpretable, predictive models that can guide experimental design and hypothesis generation in biology. The convergence of symbolic regression, neural networks, and operator-theoretic methods is expected to drive future advances, with increasing emphasis on hybrid, interpretable, and data-efficient algorithms.

Conclusion

This review provides a rigorous and critical synthesis of data-driven methods for dynamical model discovery in biology, grounded in operator-theoretic principles and benchmarked on canonical nonlinear systems. The analysis reveals that while regression-based and decomposition methods can yield interpretable models under ideal conditions, their applicability is severely constrained by data quality and system complexity. Neural network-based approaches offer greater flexibility but at the cost of interpretability and generalization. Hybrid methodologies that integrate symbolic, neural, and geometric insights represent a promising direction for future research, particularly as experimental capabilities continue to advance. The paper sets a clear agenda for the development of robust, interpretable, and scalable data-driven modeling frameworks in the life sciences.