Conformal bootstrap: from Polyakov to our times (2509.02779v1)

Abstract: We trace the history of conformal bootstrap from its early days to our times - a great example of unity of physics. We start by describing little-known details about the origins of conformal field theory in the study of strong interactions and critical phenomena in the 1960s and 1970s. We describe similarities and differences between approaches and results of the main groups in Moscow, Rome, and Sofia. Then come the breakthroughs in the 1980s and the 1990s, in particular 2D CFT and holography. Finally, we describe the genesis of the numerical conformal bootstrap, from the conformal technicolor bounds in the 2000s, to the determination of the 3D Ising critical exponents in the 2010s. We conclude with some outstanding challenges. We stress that conformal invariance is a symmetry of nature.

• The paper’s main contribution is a comprehensive review of the conformal bootstrap, detailing its evolution from Polyakov’s early proposals to current numerical methods.
• It illustrates the transition from analytic approaches in 2D CFTs to advanced semidefinite programming techniques that yield precise bounds on operator dimensions.
• The methodology emphasizes the use of analytic functionals and highlights open challenges such as uniqueness proofs and applications to higher-dimensional gauge theories.

Conformal Bootstrap: Historical Development, Methodology, and Future Directions

Introduction

The conformal bootstrap program has evolved from its origins in the paper of critical phenomena and strong interactions in the 1960s and 1970s to a central tool in modern theoretical physics, enabling nonperturbative analysis of conformal field theories (CFTs) in diverse dimensions. This essay provides a technical overview of the historical trajectory, methodological advances, and current challenges in the conformal bootstrap, as presented in "Conformal bootstrap: from Polyakov to our times" (2509.02779). The discussion is organized chronologically, highlighting key conceptual breakthroughs, the development of numerical techniques, and the implications for both statistical physics and quantum field theory.

Early History: Scale and Conformal Invariance

The initial motivation for conformal symmetry arose from attempts to understand scale invariance in high-energy hadronic interactions and critical phenomena. The seminal works of Migdal, Polyakov, and others established the relevance of anomalous scaling dimensions and the operator product expansion (OPE) in critical systems. Polyakov's 1970 paper introduced the explicit form of conformal three- and four-point functions and argued for conformal invariance at criticality, providing a nontrivial check against the 2D Ising model.

However, the "old bootstrap" approach, based on skeleton expansions consistent with conformal symmetry, was soon superseded by the renormalization group (RG) paradigm, which offered a systematic framework for critical exponents via the $\epsilon$-expansion and large-$N$ techniques. The limitations of the skeleton expansion—primarily its lack of convergence and dependence on microscopic details—were recognized by Polyakov and Wilson.

Birth of the Modern Conformal Bootstrap

Polyakov's 1974 "Non-Hamiltonian approach" marked a conceptual shift, postulating that the spectrum and OPE coefficients of primary operators should be determined by crossing symmetry of four-point functions, independent of any underlying Hamiltonian. This approach anticipated the modern conformal bootstrap, where the consistency of OPE associativity and crossing symmetry is elevated to a dynamical principle. Polyakov's implementation, based on dispersion relations and the construction of "unitary amplitudes," was technically distinct from the conformal block formalism that would later dominate.

Concurrently, the Rome group (Ferrara, Gatto, Grillo, Parisi) developed the shadow formalism and explicit conformal block expansions, emphasizing the role of crossing symmetry and positivity constraints. Mack and the Sofia group contributed rigorous classification of unitary representations and harmonic analysis on the conformal group, laying the mathematical foundation for later developments.

Two-Dimensional CFT and the BPZ Revolution

The breakthrough of Belavin, Polyakov, and Zamolodchikov (BPZ) in 1984 established the infinite-dimensional Virasoro algebra as the symmetry of 2D CFTs, enabling exact solutions for minimal models via the conformal bootstrap. The BPZ approach demonstrated that crossing symmetry, combined with the structure of Virasoro primaries and degenerate representations, yields exact scaling dimensions and OPE coefficients for models such as the 2D Ising CFT. The rationality of minimal models allowed for finite solutions to the bootstrap equations, but the extension to irrational CFTs and higher dimensions remained challenging.

Higher-Dimensional CFTs and the Advent of Numerical Bootstrap

The absence of infinite-dimensional symmetry in $d>2$ precluded exact solutions, but the development of the numerical conformal bootstrap in the 2000s revitalized the field. Motivated by phenomenological questions in particle physics (e.g., conformal technicolor), Rattazzi, Rychkov, Tonni, and Vichi introduced a method to bound operator dimensions in unitary CFTs by discretizing the crossing equations and employing linear programming techniques.

The key methodological advance was the expansion of four-point functions in global conformal blocks and the imposition of crossing symmetry via Taylor expansion around the symmetric point $z=\bar{z}=1/2$. The positivity of OPE coefficients enabled rigorous exclusion of regions in the space of scaling dimensions, leading to nontrivial bounds on operator gaps (Figure 1).

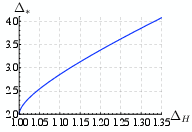
Figure 1: The bound from Rattazzi et al. [Rattazzi:2008pe], showing numerical constraints on scalar operator dimensions in 4D CFTs.

Subsequent work extended these techniques to mixed correlators, superconformal theories, and higher-order derivative expansions, culminating in the precise determination of critical exponents for the 3D Ising model.

The 3D Ising Model and Precision Bootstrap

The numerical bootstrap achieved a milestone with the isolation of the 3D Ising CFT via the identification of a "kink" in the bound on the second scalar operator, corresponding to the known critical exponents (Figure 2, Figure 3).

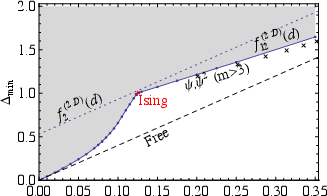
Figure 2: The $d=2$ bound from Rychkov & Vichi [Rychkov:2009ij], exhibiting a kink at the 2D Ising CFT.

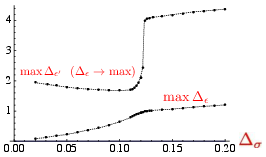
Figure 3: The bound on the second scalar with the first at the gap [Rychkov:2011et], revealing the transition from relevant to irrelevant at the kink.

The implementation of semidefinite programming and the inclusion of multiple correlators (e.g., $\langle \sigma \sigma \sigma \sigma \rangle$, $$\langle \epsilon \epsilon \epsilon \epsilon \rangle$$) led to the emergence of "islands" in parameter space, tightly constraining the allowed values of scaling dimensions and OPE coefficients (Figure 4).

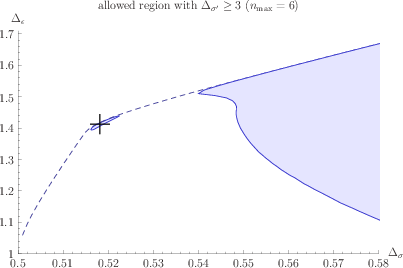
Figure 4: The first 3D Ising island [Kos:2014bka], demonstrating the power of mixed correlator bootstrap and semidefinite programming.

The accuracy of bootstrap-derived critical exponents now surpasses that of Monte Carlo and RG methods, with determinations of $\eta$ and $\nu$ at the $10^{-7}$–$10^{-8}$ level (see Table below).

Approach	$\eta$	$\nu$
Experiments	0.04(1)	0.63(1)
RG (6-loop)	0.0362(6)	0.6292(5)
Monte Carlo	0.03627(10)	0.63002(10)
CFT Bootstrap	0.036297612(48)	0.62997097(12)

Methodological Advances: Analytic Functionals and Large $\Delta$ Problem

Recent work has focused on improving the convergence of bootstrap bounds for operators with large scaling dimensions. The standard derivative functional basis exhibits slow convergence for large $\Delta$, motivating the development of analytic functionals constructed via contour integrals in the unit disk variables (Figure 5, Figure 6).

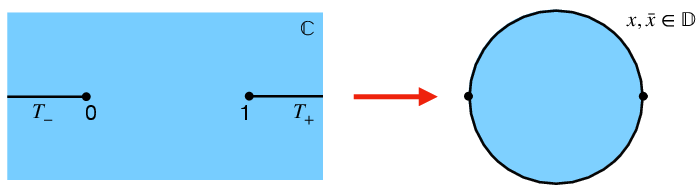
Figure 5: Analytic structure of the four-point function in $z,\bar{z}$ and $x,\bar{x}$ variables.

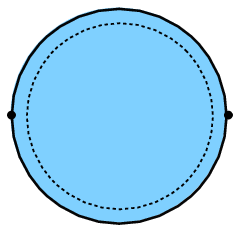
Figure 6: Contour integration yields linear functionals on analytic functions, providing a more efficient basis for the bootstrap.

The use of analytic functionals, particularly in 1D and 2D, has led to rapid convergence and improved bounds for high-dimension operators (Figure 7).

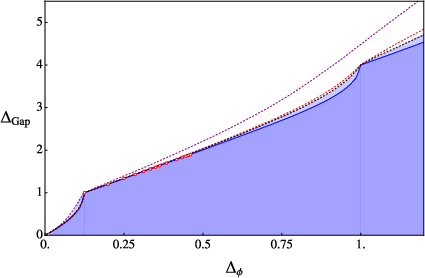
Figure 7: The 2D gap maximization bound using analytic functionals [Ghosh:2023onl], demonstrating superior convergence at large $\Delta_\phi$.

Extension to higher dimensions is ongoing, with promising preliminary results in $d=3$.

Open Problems and Future Directions

Several outstanding challenges remain:

• Uniqueness: Proving the uniqueness of the 3D Ising CFT within the allowed "island" remains open, as does the exclusion of masquerading theories with similar symmetry.
• Nonexistence: Demonstrating the absence of CFTs corresponding to first-order transitions (e.g., 3D 3-state Potts model) via bootstrap constraints is an active area.
• Gauge Theories: Bootstrapping 3D conformal gauge theories (e.g., QED$_3$) is complicated by large operator dimensions and slow convergence.
• Large $\Delta$: Systematic resolution of the large $\Delta$ problem via analytic functionals and improved numerical techniques is a key technical frontier.

Implications and Speculation

The conformal bootstrap has established conformal invariance as an emergent symmetry in nature, with experimental and numerical data for critical exponents in diverse universality classes matching bootstrap predictions to high precision. The methodology is now central to both statistical physics and quantum field theory, with applications ranging from condensed matter to particle phenomenology and holography.

Future developments are likely to include:

• Automated classification and isolation of CFTs via high-dimensional bootstrap.
• Extension of analytic functional techniques to $d>2$ and spinning correlators.
• Rigorous proofs of uniqueness and nonexistence for universality classes.
• Integration with machine learning and optimization for large-scale bootstrap computations.

Conclusion

The conformal bootstrap program, from its origins in the 1970s to its current status as a precision tool for nonperturbative quantum field theory, exemplifies the unity of physics and the power of symmetry principles. The interplay between historical insight, mathematical rigor, and computational innovation continues to drive progress, with the bootstrap poised to address fundamental questions about the structure and classification of quantum field theories.