First Principles Quantization of a Non-Conservative Scalar Field (2509.01403v1)

Abstract: We present the first-principles quantization of a damped scalar field within the framework of classical action principle of non-conservative systems using doubled dynamical variables. We consider a non-conservative potential term constructed to describe a linear damping of the scalar field for quantization using canonical and path-integral formalisms, and derive the two-point Green's function along with the spectral function, which are consistent with known results from the well-known in-in formalism.

• The paper presents a novel first-principles quantization using a doubled-variables action principle to address non-conservative, dissipative dynamics.
• It derives both the path integral and canonical quantization approaches, yielding a Hermitian Hamiltonian and consistent Green's functions.
• The framework accurately describes finite lifetimes for quasi-scalar bosons, bridging classical dissipative behavior with quantum coherence.

First-Principles Quantization of a Non-Conservative Scalar Field

Introduction and Motivation

The quantization of non-conservative systems, particularly those exhibiting dissipation, remains a fundamental challenge in both classical and quantum field theory. Traditional action principles and canonical quantization procedures are inherently time-symmetric and thus ill-suited for systems with explicit time-asymmetry, such as those with linear damping. While effective approaches—such as the Lindblad formalism and phenomenological modifications to the Lagrangian—have been widely used, they lack a rigorous first-principles foundation and often fail to preserve unitarity or the uncertainty principle. The work under discussion addresses this gap by providing a first-principles quantization of a damped scalar field, leveraging the doubled-variables action principle introduced by Galley, and systematically deriving the quantum theory using both path-integral and canonical approaches.

Classical Framework: Doubling of Variables and Non-Conservative Action

The starting point is the classical action principle for non-conservative systems, which requires doubling the field degrees of freedom: $\Phi \rightarrow (\Phi_1, \Phi_2)$. The action is constructed as

$$S[\Phi_a] = \int d^4x\,\Lambda(\Phi_a, \partial_\mu\Phi_a), \quad a=1,2,$$

where the Lagrangian density $\Lambda$ contains both conservative and non-conservative contributions:

$$\Lambda(\Phi_a, \partial_\mu\Phi_a) = \mathcal{L}(\Phi_1, \partial_\mu\Phi_1) - \mathcal{L}(\Phi_2, \partial_\mu\Phi_2) + \mathcal{K}(\Phi_{1,2}, \partial_\mu\Phi_{1,2}).$$

The non-conservative term $\mathcal{K}$ is constructed to yield the correct dissipative dynamics in the physical limit, where $\Phi_1 = \Phi_2$. For a real scalar field with linear damping, the model Lagrangian is

$$\Omega(\phi_{1,2}, \partial_\mu\phi_{1,2}) = \frac{1}{2}\partial_\mu\phi_1\partial^\mu\phi_1 - \frac{1}{2}m^2\phi_1^2 - \left(\frac{1}{2}\partial_\mu\phi_2\partial^\mu\phi_2 - \frac{1}{2}m^2\phi_2^2\right) - \frac{\gamma}{2}(\phi_1 - \phi_2)(\partial_0\phi_1 + \partial_0\phi_2).$$

This construction leads to the damped Klein-Gordon equation:

$$\partial_t^2\phi(x,t) - \nabla^2\phi(x,t) + m^2\phi(x,t) + \gamma\partial_t\phi(x,t) = 0.$$

Path Integral Quantization and Green's Functions

The path integral formulation is facilitated by transforming to the $(\phi_+, \phi_-)$ basis, where $\phi_+ = (\phi_1 + \phi_2)/2$ and $\phi_- = \phi_1 - \phi_2$. The action in momentum space becomes quadratic:

$$S[\tilde\phi_+, \tilde\phi_-] = \int \frac{d^4k}{(2\pi)^4} \tilde\phi_+(k)[k^2 - m^2 - i\gamma k^0]\tilde\phi_-(-k).$$

The resulting kernel $M(k)$ is off-diagonal, and its inverse yields the retarded and advanced Green's functions:

$$\tilde G_{\mathrm{ret}}(k) = \frac{1}{k^2 - m^2 + i\gamma k^0}, \qquad \tilde G_{\mathrm{adv}}(k) = \frac{1}{k^2 - m^2 - i\gamma k^0}.$$

The dissipative term $i\gamma k^0$ shifts the poles of the propagator off the real axis, encoding the causal structure and finite lifetime of excitations.

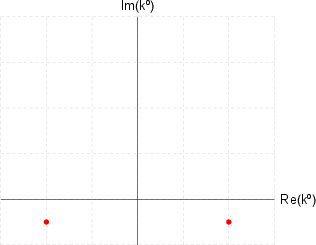
Figure 1: (a) The pole of the retarded Green's function is shifted just below the real axis; (b) the pole of the advanced Green's function is shifted just above the real axis.

The spectral function,

$$\rho(k^2) = \frac{1}{\pi} \frac{\gamma k^0}{[(k^0)^2 - E_{\vec{k}}^2]^2 + \gamma^2 (k^0)^2},$$

peaks at $k^0 \approx E_{\vec{k}}$ with width $\gamma$, corresponding to a quasi-scalar boson with lifetime $\tau \sim 1/\gamma$. In the limit $\gamma \to 0$, the standard free-field spectral function is recovered.

Canonical Quantization and Fock Space Structure

Canonical quantization proceeds by promoting the fields and their conjugate momenta to operators and imposing equal-time commutation relations. The mode expansions for the physical ($\phi_+$) and auxiliary ($\phi_-$) fields are \begin{align*} \phi_+(x) &= e^{-\frac{\gamma}{2}t} \int \frac{d^3\mathbf{k}}{(2\pi)^3\sqrt{\omega_k}} [b(\mathbf{k})e^{-ik\cdot x} + b^\dagger(\mathbf{k})e^{ik\cdot x}], \ \phi_-(x) &= e^{+\frac{\gamma}{2}t} \int \frac{d^3\mathbf{k}}{(2\pi)^3\sqrt{\omega_k}} [a(\mathbf{k})e^{-ik\cdot x} + a^\dagger(\mathbf{k})e^{ik\cdot x}], \end{align*} with $\omega_{\vec{k}}^2 = \vec{k}^2 + m^2 - \gamma^2/4$. The only non-vanishing commutators are $$[a(\mathbf{k}), b^\dagger(\mathbf{p})] = (2\pi)^3\delta^3(\mathbf{k} - \mathbf{p})$$ and its Hermitian conjugate, reflecting the mixing of physical and auxiliary sectors.

The normal-ordered Hamiltonian is

$$:H: = \int \frac{d^3p}{(2\pi)^3} \left[(\omega_{\vec{p}} + i\frac{\gamma}{2}) b^\dagger(\vec{p}) a(\vec{p}) + (\omega_{\vec{p}} - i\frac{\gamma}{2}) a^\dagger(\vec{p}) b(\vec{p})\right],$$

which is manifestly Hermitian. The time evolution of the physical creation operator is

$$b^\dagger(\vec{k}, t) = e^{i\omega_{\vec{k}} t} e^{-\frac{\gamma}{2} t} b^\dagger(\vec{k}, 0),$$

implying that physical one-particle states decay exponentially with lifetime $1/\gamma$.

Physical and Auxiliary States

Physical states are constructed by acting with $b^\dagger$ on the vacuum, while auxiliary states are generated by $a^\dagger$. The normalization condition involves both sectors:

$$\langle \vec{k}_- | \vec{p}_+ \rangle = (2\pi)^3 \delta^3(\vec{k} - \vec{p}).$$

The auxiliary sector is essential for normalization and the preservation of probability, but does not correspond to observable excitations. The physical sector describes quasi-scalar bosons with finite lifetimes, a direct quantum analog of classical dissipative decay.

Implications and Future Directions

This work provides a rigorous, first-principles quantization of a non-conservative scalar field, establishing consistency with the Schwinger-Keldysh (in-in) formalism and clarifying the structure of dissipative quantum field theories. The explicit construction of the Hamiltonian, Green's functions, and spectral properties demonstrates that dissipation can be incorporated without ad hoc modifications or loss of unitarity at the operator level. The distinction between physical and auxiliary sectors is crucial for both normalization and the interpretation of decay processes.

The formalism is directly applicable to a range of problems in nonequilibrium quantum field theory, open quantum systems, and cosmology, where dissipative effects are significant. The approach also provides a foundation for the systematic paper of more complex non-conservative interactions, including those relevant to inflationary dynamics and quantum gravity. Future work may extend these methods to tensor fields, gauge theories, and systems with nonlinear dissipation, as well as explore the interplay between dissipation and quantum coherence in early-universe scenarios.

Conclusion

The first-principles quantization of a damped scalar field using the doubled-variables action principle yields a consistent quantum theory of dissipation, with well-defined Green's functions, spectral properties, and a Hermitian Hamiltonian. The formalism bridges classical and quantum treatments of non-conservative systems and provides a robust framework for further theoretical and phenomenological investigations of dissipative quantum field dynamics.