Flat Space Holography via AdS/BCFT (2509.00652v1)

Abstract: In this paper, we study a new class of AdS/BCFT setups, where the world-volumes of end-of-the-world branes (EOW branes) are given by flat spaces, to explore flat space holography from an AdS bulk. We show that they provide gravity duals of CFTs in the presence of null boundaries. Our holographic calculations lead to many new predictions on entanglement entropy, correlation functions and partition functions for CFTs with null boundaries. By considering a bulk region between two EOW branes, we present an AdS/BCFT explanation that the flat space gravity is dual to a Carrollian CFT (CCFT), including the swing surface calculation of entanglement entropy.

• The paper introduces a novel methodology embedding flat space holography into the AdS/BCFT framework via flat EOW branes to enable controlled calculations of entanglement entropy and correlation functions.
• It analyzes three setups (Type I, II, III) that reveal distinct holographic dualities, including a non-unitary dual with complex entanglement entropy and a correspondence to Carrollian CFTs.
• The work bridges field theory and gravity by matching holographic calculations with BCFT behavior on null boundaries, paving the way for deeper studies in flat space and celestial holography.

Flat Space Holography via AdS/BCFT: A Technical Analysis

Introduction and Motivation

The paper "Flat Space Holography via AdS/BCFT" (2509.00652) develops a new approach to flat space holography by embedding it within the AdS/BCFT framework. The central innovation is the use of end-of-the-world (EOW) branes with flat worldvolumes in AdS, which, via brane-world holography, provide a controlled setting to paper the duality between gravity in flat spacetime and field theories on null boundaries. This construction enables explicit holographic calculations of entanglement entropy, correlation functions, and partition functions for CFTs with null boundaries, and clarifies the relationship between flat space gravity and Carrollian CFTs (CCFTs).

AdS/BCFT with Flat EOW Branes: Geometric Construction

The AdS/BCFT correspondence posits that a $d$-dimensional BCFT is dual to a region of AdS$_{d+1}$ bounded by the conformal boundary and an EOW brane. The EOW brane's tension $T$ determines its induced geometry: AdS, dS, or flat. The focus here is on the flat case, $|T| = \frac{d-1}{R}$, where the brane is dual to a null boundary in the BCFT.

The explicit embedding of the flat EOW brane is constructed in both Poincaré and global AdS coordinates. In Poincaré coordinates, the brane is simply $z = z_0$, yielding a flat induced metric. In global coordinates, the brane's intersection with the AdS boundary defines a diamond-shaped region bounded by null surfaces.

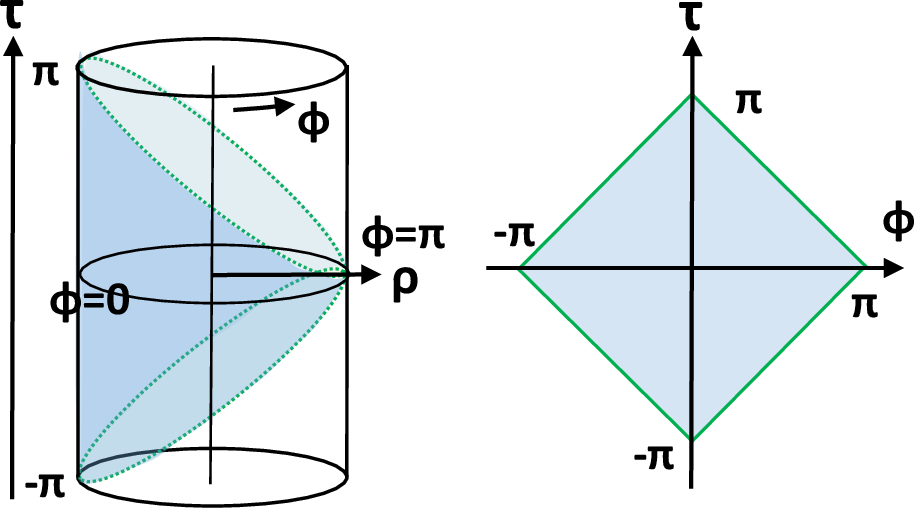
Figure 1: A sketch of Poincaré AdS inside global AdS (left) and the boundary of Poincaré AdS (right) in the $(\tau, \phi)$ coordinate.

Figure 2: Profile of a flat EOW brane in Lorentzian (left) and Euclidean (right) global AdS. $R > z_0$ is assumed.

Three Holographic Setups: Type I, II, and III

Three distinct configurations are analyzed:

• Type I: The AdS region between the conformal boundary and a single flat EOW brane ($0 < z < z_0$). The dual is a CFT on a diamond with null boundaries, interpreted as final state projections.
• Type II: The AdS region outside the flat EOW brane ($z > z_0$). The dual is a CFT coupled to flat space gravity on the diamond, realizing the Flat/CCFT correspondence.
• Type III: The region between two flat EOW branes ($z_1 < z < z_2$), isolating the null boundaries. The dual is a CCFT living on the null edges, corresponding to wedge holography.

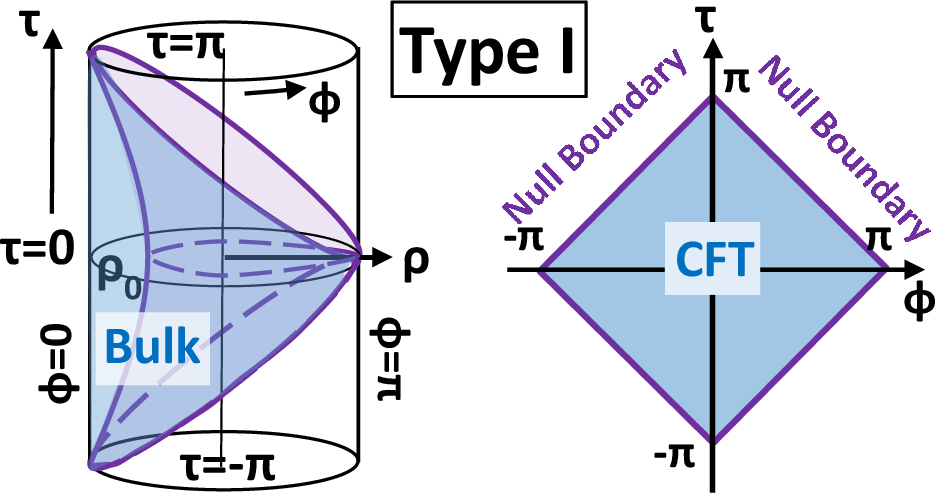
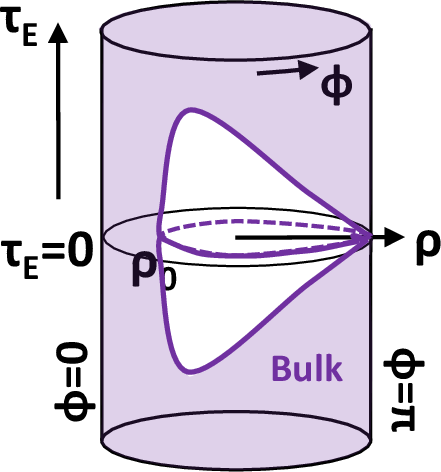
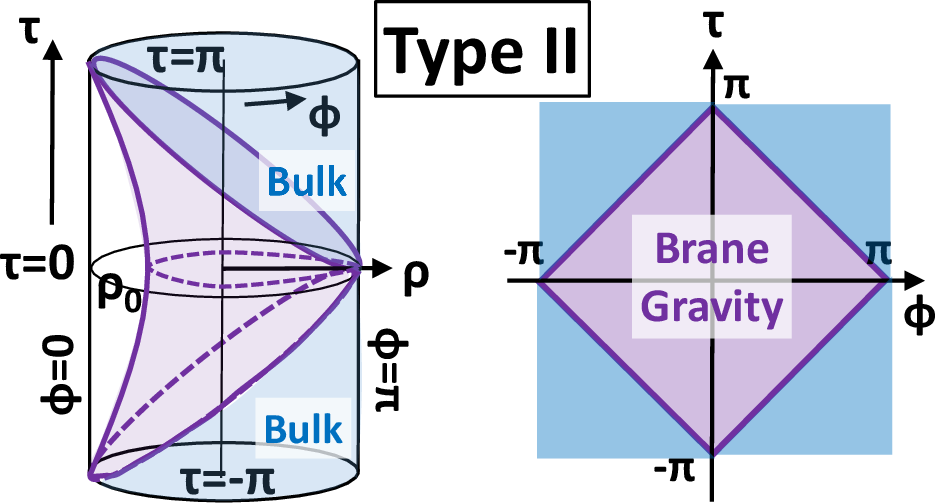
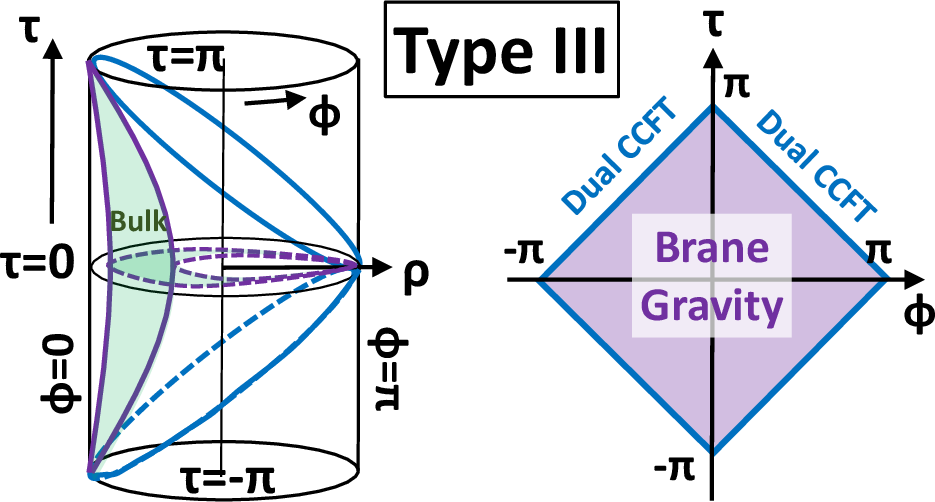
Figure 3: Sketches of the three setups: type I, II, and III. Left: gravity dual regions in global AdS. Middle: dual 2D theories. Right: Euclidean setups.

Holographic Entanglement Entropy

The entanglement entropy is computed using the Ryu-Takayanagi prescription, with extremal surfaces allowed to end on the EOW brane. Two classes of extremal surfaces arise: connected (anchored on the entangling surface) and disconnected (anchored on both the entangling surface and the EOW brane).

Figure 4: Holographic entanglement entropy in type I (left) and type II (right) setups for AdS$_3$. Connected (green) and disconnected (red) geodesics are shown.

• Type I: The disconnected geodesic is always spacelike, and the entanglement entropy is real. The minimal surface is determined by comparing the connected and disconnected contributions.
• Type II: The disconnected geodesic generically includes both spacelike and timelike segments, leading to a complex-valued (pseudo) entropy. The imaginary part is $\frac{\pi}{2G_N}i$, analogous to time-like entanglement entropy, and signals a non-Hermitian dual density matrix. This is a strong claim: the dual theory for flat space gravity on the brane is non-unitary, despite the unitarity of the bulk gravity theory.

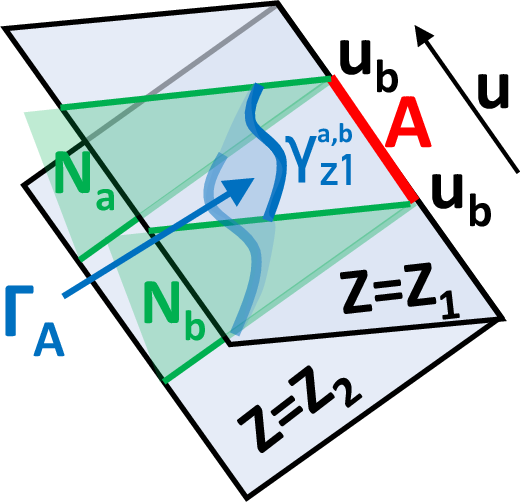
  Figure 5: Holographic entanglement entropy in type III. Two EOW branes at $z=z_1$ and $z=z_2$ intersect at the AdS boundary; the extremal surface $\Gamma_A$ stretches between null surfaces $N_a$ and $N_b$, reproducing the swing surface prescription for CCFT.

• Type III: The entanglement entropy reduces to the swing surface prescription of Flat/CCFT holography, with the extremal surface determined by null modular flow and area minimization. The result matches the expected CCFT$_2$ entanglement structure, with $c_L = 0$ and $c_M = \frac{3}{G_N}(\frac{1}{z_1} - \frac{1}{z_2})$.

Holographic Correlation Functions

Two-point and one-point functions are computed using bulk-to-boundary propagators, with boundary conditions imposed on the EOW brane.

• Type I: Dirichlet or Neumann conditions at $z = z_0$ yield modified two-point functions. For Dirichlet, the two-point function decays exponentially as one operator approaches the null boundary, indicating that the null boundary acts as a final state projection, removing degrees of freedom.
• Type II: The two-point function differs from type I by an overall phase $e^{2\pi i \nu}$, but the real-space structure is otherwise identical. The one-point function also acquires a phase $e^{\pi i \Delta}$ compared to type I.

The saddle point approximation for large conformal dimension $\Delta$ shows that the disconnected geodesic contribution to entanglement entropy matches the leading behavior of the one-point function of the twist operator, confirming the consistency of the holographic and field-theoretic calculations.

Bulk Spectrum and Flat Space Reduction

In type III, the spectrum of a bulk scalar field with Neumann conditions at $z_1$ and $z_2$ is quantized as $q_n = \frac{n\pi}{L}$ for AdS$_4$, with $L = z_2 - z_1$. This demonstrates that the bulk theory reduces to a tower of massive fields in flat space, matching expectations from flat space holography and CCFT correspondence.

On-Shell Action and Partition Functions

The Euclidean on-shell action is computed in Poincaré AdS$_3$ with a flat EOW brane, regularized by either a deformed cutoff surface or by approaching the flat brane as a limit of AdS branes. The result is

$$I_{tot} = -\frac{1}{4G_N} \log \frac{z_0}{\epsilon}$$

for both type I and II, up to sign. This matches the expected behavior of the boundary entropy (the $g$-function) in the $T \to \pm 1$ limit, where $\log g \to \mp \infty$.

Euclidean Flat Space Holography

In the Euclidean setup, the flat EOW brane intersects the AdS boundary at a single point. The dual theory is localized on a $d$-dimensional ball of vanishing size, and the on-shell action scales as $e^{\frac{d}{2}\rho_\infty}$, suggesting a duality between flat space gravity on a ball and a point-like theory. This is a novel realization of flat space holography in the Euclidean context.

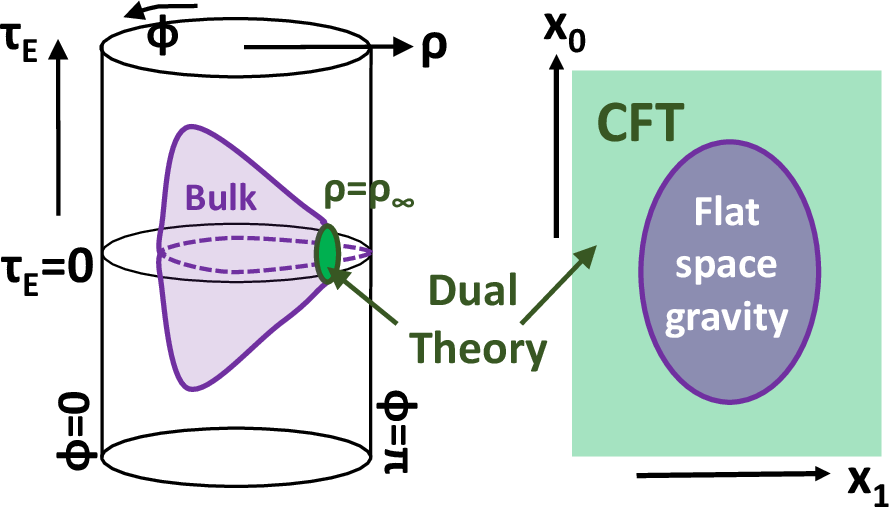
Figure 6: Euclidean type II setup with a UV cutoff (left) and its dual field theory description via double holography (right) in Poincaré coordinates.

Field Theory Analysis: Null Boundaries in BCFT

Appendix A provides a field-theoretic analysis of BCFTs with null boundaries. For a free scalar, the one-point function vanishes and the two-point function reduces to the bulk CFT result, confirming that null boundaries act as final state projections. Analytical continuation and moving mirror setups further corroborate this behavior.

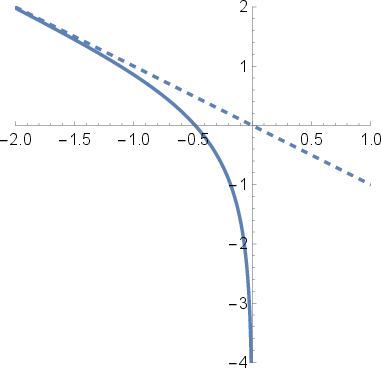
Figure 7: The solid line is the location of the moving mirror, while the dashed line is the null boundary.

Implications and Future Directions

This work provides a systematic, calculable framework for flat space holography within the well-understood AdS/BCFT paradigm. The explicit construction of flat EOW branes and the associated holographic dictionary yield several strong results:

• Non-unitarity of the dual theory for flat space gravity on the brane, as evidenced by complex entanglement entropy.
• Precise matching between holographic and field-theoretic calculations for entanglement and correlation functions in the presence of null boundaries.
• Reduction to CCFTs in the type III setup, justifying the Flat/CCFT correspondence from a top-down AdS perspective.
• Euclidean realization of flat space holography as a duality between flat space gravity and a point-like theory.

Potential future developments include a deeper analysis of the non-unitary structure of the dual theory, the role of complex geodesics in entanglement calculations, and connections to celestial holography and other approaches to flat space holography.

Conclusion

By embedding flat space holography into the AdS/BCFT framework with flat EOW branes, this work provides a concrete, calculable realization of holography for gravity in flat spacetime. The results clarify the structure of dual field theories with null boundaries, establish the connection to CCFTs, and open new avenues for the paper of non-unitary holographic dualities and the interplay between AdS and flat space holography.