AdaptFlow: Adaptive Workflow Optimization via Meta-Learning (2508.08053v1)

Abstract: Recent advances in LLMs have sparked growing interest in agentic workflows, which are structured sequences of LLM invocations intended to solve complex tasks. However, existing approaches often rely on static templates or manually designed workflows, which limit adaptability to diverse tasks and hinder scalability. We propose AdaptFlow, a natural language-based meta-learning framework inspired by model-agnostic meta-learning (MAML). AdaptFlow learns a generalizable workflow initialization that enables rapid subtask-level adaptation. It employs a bi-level optimization scheme: the inner loop refines the workflow for a specific subtask using LLM-generated feedback, while the outer loop updates the shared initialization to perform well across tasks. This setup allows AdaptFlow to generalize effectively to unseen tasks by adapting the initialized workflow through language-guided modifications. Evaluated across question answering, code generation, and mathematical reasoning benchmarks, AdaptFlow consistently outperforms both manually crafted and automatically searched baselines, achieving state-of-the-art results with strong generalization across tasks and models. The source code and data are available at https://github.com/microsoft/DKI_LLM/tree/AdaptFlow/AdaptFlow.

• The paper introduces a bi-level meta-learning framework that refines LLM-based workflows via symbolic textual feedback and binary update signals.
• It employs K-Means clustering and structured prompt engineering to enable subtask-specific adaptation and robust meta-optimization.
• It outperforms static and manual baseline methods, demonstrating state-of-the-art accuracy on math benchmarks while ensuring model-agnostic deployment.

AdaptFlow: Adaptive Workflow Optimization via Meta-Learning

Introduction and Motivation

AdaptFlow introduces a meta-learning framework for agentic workflow optimization, targeting the automation and generalization of LLM-based workflows across heterogeneous tasks. The motivation stems from the limitations of static or manually designed agentic workflows, which lack adaptability and scalability when deployed on diverse datasets. Prior approaches, such as ADAS and AFLOW, either generate a single static workflow or rely on coarse-grained updates, resulting in suboptimal generalization and convergence issues in code-based search spaces. AdaptFlow addresses these challenges by leveraging principles from Model-Agnostic Meta-Learning (MAML), enabling rapid subtask-level adaptation and robust meta-optimization in symbolic code spaces.

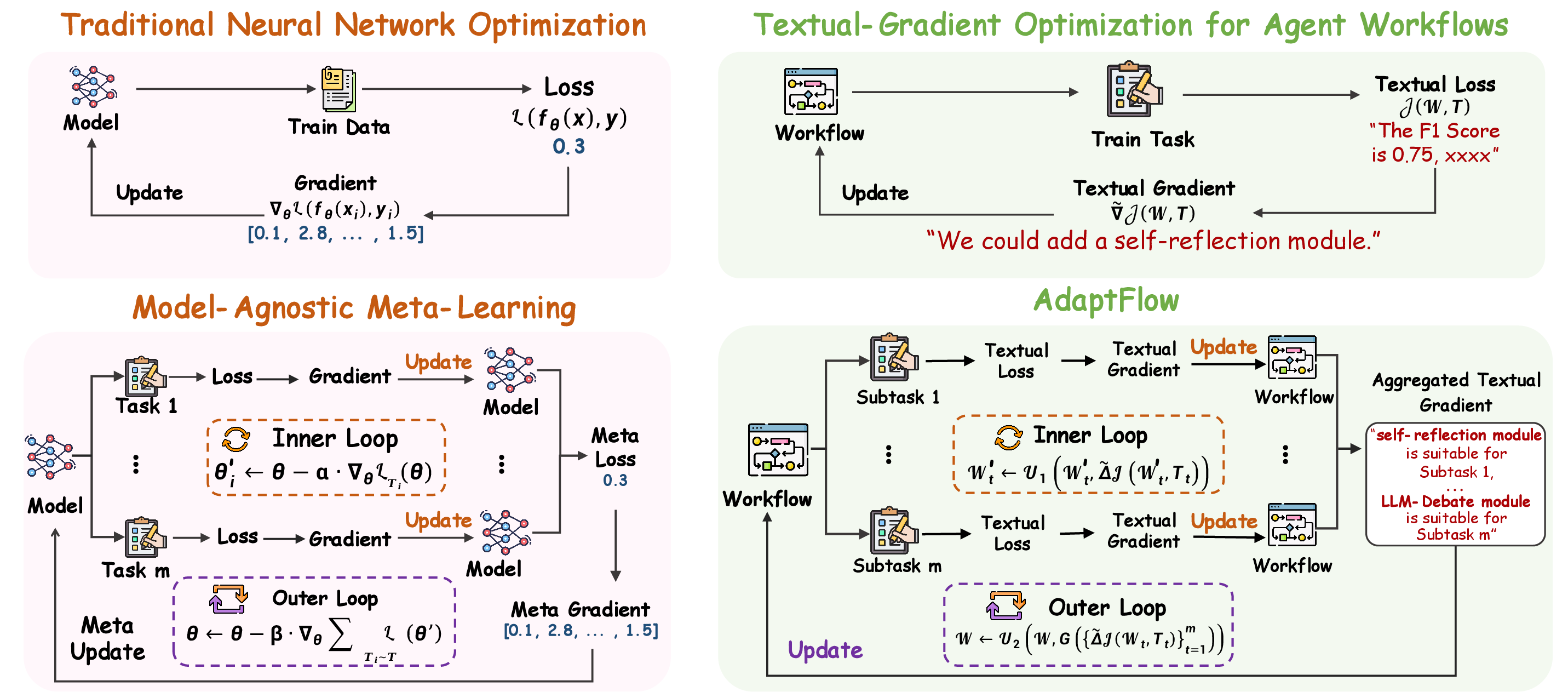
Figure 1: An analogy between Neural Network Optimization and Workflow Optimization, as well as between MAML and AdaptFlow.

Methodology

Bi-Level Meta-Optimization Framework

AdaptFlow operates via a bi-level optimization scheme:

• Inner Loop: For each semantically clustered subtask, the workflow is iteratively refined using LLM-generated textual feedback, which serves as a symbolic gradient. Updates are applied only if a binary continuation signal indicates non-trivial performance improvement, mitigating instability from long-context accumulation.
• Outer Loop: Aggregates subtask-level improvements into a shared workflow initialization. A reflection step revisits failure cases, generating further refinement suggestions to enhance robustness and convergence.

This design enables both effective subtask-specific adaptation and stable convergence in discrete code spaces.

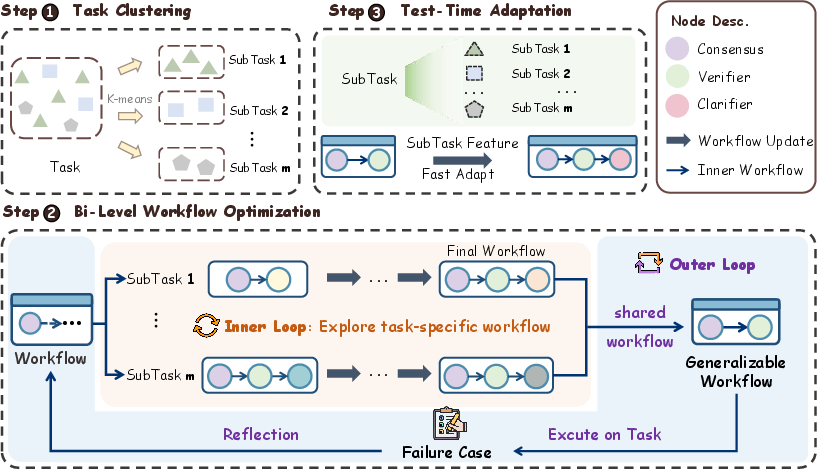
Figure 2: Illustration of the AdaptFlow framework, consisting of three stages: task clustering, bi-level workflow optimization, and test-time adaptation.

Task Clustering

Training tasks are partitioned into semantically coherent subtasks using K-Means clustering over instruction embeddings (all-MiniLM-L6-v2). This decomposition supports focused workflow specialization and stable learning.

Test-Time Adaptation

At inference, unseen tasks are clustered, and subtask-level semantic descriptions are generated from input prompts. The global workflow is rapidly adapted via LLM-guided symbolic updates, leveraging these descriptions for specialization without access to ground-truth answers.

Prompt Engineering

AdaptFlow employs structured prompt templates for inner loop, outer loop, reflection, and test-time adaptation, ensuring reliable and interpretable workflow updates. Prompts are designed to elicit actionable feedback and complete code snippets for agentic modules.

Experimental Results

Benchmarks and Baselines

AdaptFlow is evaluated on eight public datasets spanning question answering, code generation, and mathematical reasoning. Baselines include manually designed workflows (Vanilla, CoT, Reflexion, LLM Debate, Step-back Abstraction, Quality Diversity, Dynamic Assignment) and automated methods (ADAS, AFLOW).

Performance

AdaptFlow achieves the highest overall average score (68.5) across all domains, outperforming both manual and automated baselines. Notably, it delivers substantial gains on mathematics benchmarks, demonstrating superior handling of complex symbolic and multi-step reasoning.

Ablation Studies

• Reflection Module: Incorporating reflection in the outer loop yields consistent performance improvements (final accuracy 61.5 vs. 60.2 without reflection).
• Test-Time Adaptation: Removing adaptation results in a drop in accuracy across all math subtasks, with the largest gain in Number Theory (68.3 to 73.9).

Convergence Analysis

The inner loop exhibits fluctuations due to long-context dependencies and the large workflow search space, but the constrained update mechanism maintains reasonable performance. The outer loop shows steady improvement by aggregating best-performing workflows, ensuring stable meta-level updates.

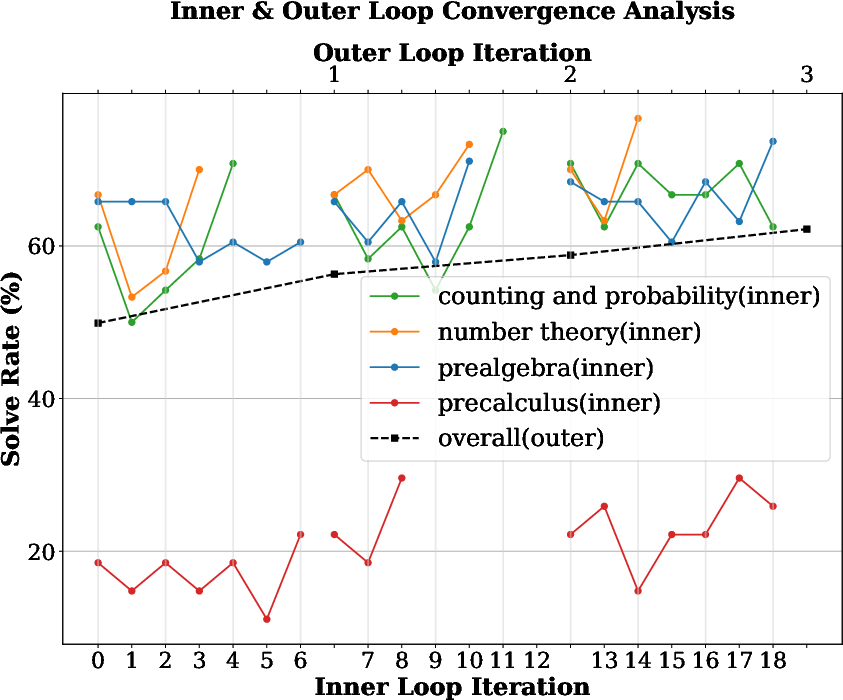
Figure 3: Convergence behavior of the inner and outer optimization loops on the MATH dataset. The inner loop fluctuates, while the outer loop steadily improves overall performance.

Model-Agnostic Generalization

AdaptFlow demonstrates strong robustness across multiple LLM backbones (GPT-4o-mini, GPT-4o, Claude-3.5-Sonnet, DeepSeek-V2.5), consistently outperforming all baselines without model-specific customization.

Case Study: Modular Workflow Design

Analysis of module usage across MATH subtasks reveals a shared front-end (Diverse Agents, Answer Extraction, Consensus) and selective introduction of task-specific modules (e.g., Approximation Detector for Prealgebra, Value Tracker for Number Theory). The outer loop consolidates subtask-specific refinements into a generalizable workflow, supporting both generalization and specialization.

Implementation Considerations

Computational Requirements

AdaptFlow requires repeated LLM queries for feedback generation and workflow execution, incurring non-trivial computational costs. Decoupling optimization and execution allows for flexible deployment across different LLM backbones.

Limitations

• The precision of symbolic updates is contingent on the quality of LLM-generated feedback, which may be insufficiently detailed for complex failure cases.
• The meta-optimization process is resource-intensive due to frequent LLM invocations.

Deployment Strategies

AdaptFlow's modular architecture and prompt-driven update mechanism facilitate integration into existing agentic systems. The framework is model-agnostic and can be adapted to new domains by retraining on relevant subtasks and customizing prompt templates.

Theoretical and Practical Implications

AdaptFlow generalizes meta-learning principles to symbolic workflow optimization, bridging the gap between differentiable model training and discrete agentic system design. The use of textual gradients and bi-level optimization enables interpretable, scalable, and adaptive workflow construction. Practically, AdaptFlow offers a robust solution for automating LLM workflow design, supporting rapid adaptation to diverse tasks and strong generalization across models.

Future Directions

Potential avenues for improvement include:

• Enhancing feedback granularity via structured or programmatic LLM outputs.
• Reducing computational overhead through more efficient adaptation strategies, such as batch updates or feedback caching.
• Extending the framework to multi-agent collaboration and tool integration scenarios.

Conclusion

AdaptFlow presents a principled meta-learning approach for adaptive agentic workflow optimization, achieving state-of-the-art results across multiple domains and demonstrating strong generalization and robustness. Its bi-level optimization, modular design, and model-agnostic architecture position it as a scalable solution for automating LLM workflow construction in real-world applications.