Computing with Canonical Microcircuits (2508.06501v1)

Abstract: The human brain represents the only known example of general intelligence that naturally aligns with human values. On a mere 20-watt power budget, the brain achieves robust learning and adaptive decision-making in ways that continue to elude advanced AI systems. Inspired by the brain, we present a computational architecture based on canonical microcircuits (CMCs) - stereotyped patterns of neurons found ubiquitously throughout the cortex. We implement these circuits as neural ODEs comprising spiny stellate, inhibitory, and pyramidal neurons, forming an 8-dimensional dynamical system with biologically plausible recurrent connections. Our experiments show that even a single CMC node achieves 97.8 percent accuracy on MNIST, while hierarchical configurations - with learnable inter-regional connectivity and recurrent connections - yield improved performance on more complex image benchmarks. Notably, our approach achieves competitive results using substantially fewer parameters than conventional deep learning models. Phase space analysis revealed distinct dynamical trajectories for different input classes, highlighting interpretable, emergent behaviors observed in biological systems. These findings suggest that neuromorphic computing approaches can improve both efficiency and interpretability in artificial neural networks, offering new directions for parameter-efficient architectures grounded in the computational principles of the human brain.

• The paper introduces a novel architecture that models canonical microcircuits with biologically plausible dynamics and neural ODEs to achieve high accuracy (97.8% on MNIST).
• It employs second-order differential equations and nODE solvers to simulate interactions among spiny stellate, inhibitory, and pyramidal neurons, mirroring cortical processes.
• Experimental results demonstrate parameter efficiency and dynamic phase space trajectories, highlighting class-specific attractors in visual data processing.

Computing with Canonical Microcircuits

Introduction

This paper introduces a novel computational architecture inspired by the human brain using Canonical Microcircuits (CMCs) framed as Neural Ordinary Differential Equations (nODEs). CMCs are ubiquitous neural patterns within the cortex, and this framework models them as biologically plausible dynamical systems incorporating spiny stellate, inhibitory, and pyramidal "neurons." Unlike conventional deep learning models, which often abstract biological details, this approach embeds neurobiological principles, potentially enhancing efficiency and interpretability in AI systems.

Neural Dynamics and Model Implementation

The foundational model employs canonical microcircuit dynamics using second-order differential equations to simulate different neuronal populations, including spiny stellate cells, inhibitory interneurons, and pyramidal cells. Each neuronal population's post-synaptic membrane potential is described by discrete equations with recurrent connectivity:

$$\ddot{v}_1 + 2\kappa_e\dot{v}_1 = \kappa_1 H_e(-\gamma_2\delta(v_4) + \gamma_1\delta(v_1) - \gamma_5\delta(v_2) + I)$$

This model is trained using nODE solvers, initially utilizing a 4th-order Runge-Kutta method, though simpler methods like Euler's are also experimented with to optimize computational efficiency.

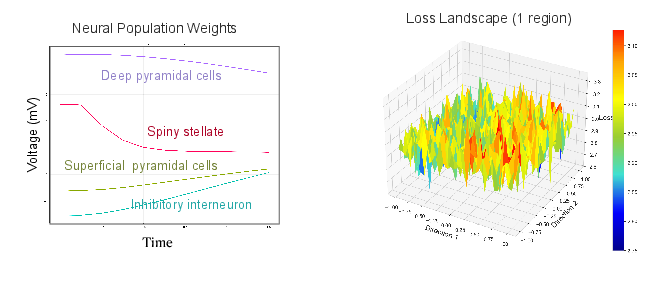
Figure 1: Single CMC node. Voltage dynamics over time, and 3D loss landscape for a single-region CMC model on MNIST.

Hierarchical Visual Processing

Visual data processing in this architecture begins with a retinal preprocessing model designed to biologically simulate early-stage processing observed in the human eye. This includes center-surround receptive fields and parallel ON/OFF pathways. Further visual processing is modeled through a hierarchy of CMCs replicating regions like V1 to V5 in the visual cortex, with configurable connectivity patterns allowing adaptive inter-node signal interactions.

Experimental Validation

Experiments conducted on MNIST and CIFAR-10 datasets illustrate that a single CMC node achieves notable accuracy (97.8% on MNIST). Hierarchical configurations further improve performance through enhanced abstract feature representation across visual tasks. Parameter efficiency is a primary strength, showcasing competitive accuracy with significantly fewer parameters than conventional deep learning architectures (Figure 2).

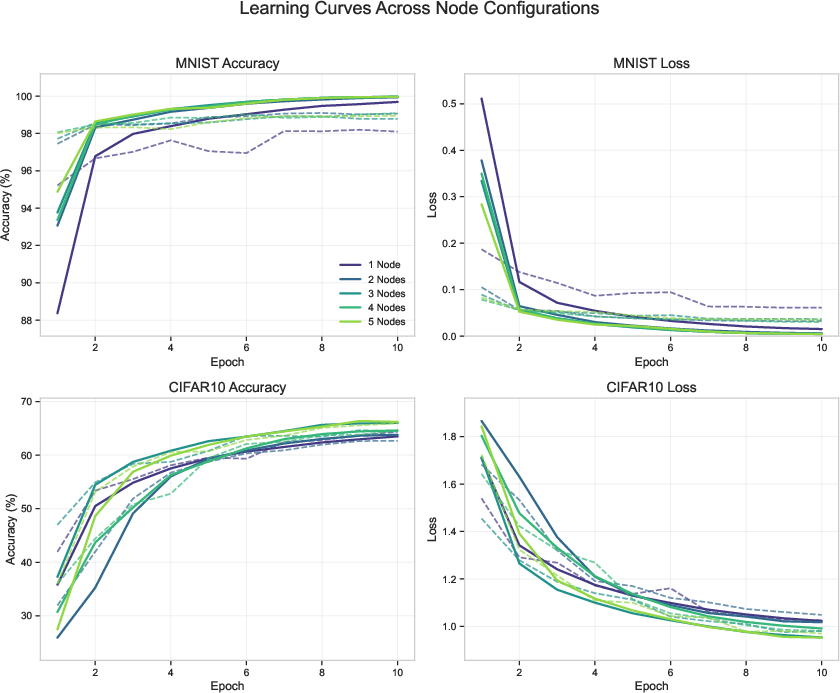
Figure 2: Top row: Accuracy and learning curves for CMC models with 1–5 regions on MNIST and CIFAR-10.

The paper performs rigorous ablation analyses, evaluating the impact of various neuron populations and recurrent connections on performance. Results show that removing recurrent connections leads to rugged loss surfaces, highlighting the importance of dynamic inter-regional connectivity for robust feature extraction (Figures 10 and 11).

Phase Space Analysis and Dynamic Representations

Phase space analysis of the model’s dynamics reveals distinct trajectories for different input classes. These emergent behaviors correlate with biological systems, where neural activity converges on class-specific attractors. The model replicates the progression of voltage activity during training, moving from random fluctuations to structured, class-dependent patterns indicative of learned representations.

Figure 3: Phase portraits of superficial pyramidal cell activity for digits 1 (blue) and 3 (orange) across different CMC node counts (1-5).

Future Directions

The architecture signals pathways forward in AI by integrating neuromodulation and extending to biologically plausible training mechanisms, such as local Hebbian updates. Expanding the model to incorporate additional sub-cortical processing stages could further mirror human visual efficiencies. The framework’s modularity permits potential extensions into more complex neural ODE formulations, such as augmented or controlled differential equations, enhancing computational capabilities.

Conclusion

This research demonstrates the viability of biologically-inspired neural architectures in yielding efficient, interpretable models competitive across standard vision benchmarks. The paper offers substantial contributions to the AI community, positing CMC-based neural dynamics as integral components in modern deep learning task frameworks, opening avenues for interdisciplinary explorations between AI and neuroscience.