Decomposing Representation Space into Interpretable Subspaces with Unsupervised Learning (2508.01916v1)

Abstract: Understanding internal representations of neural models is a core interest of mechanistic interpretability. Due to its large dimensionality, the representation space can encode various aspects about inputs. To what extent are different aspects organized and encoded in separate subspaces? Is it possible to find these natural'' subspaces in a purely unsupervised way? Somewhat surprisingly, we can indeed achieve this and find interpretable subspaces by a seemingly unrelated training objective. Our method, neighbor distance minimization (NDM), learns non-basis-aligned subspaces in an unsupervised manner. Qualitative analysis shows subspaces are interpretable in many cases, and encoded information in obtained subspaces tends to share the same abstract concept across different inputs, making such subspaces similar tovariables'' used by the model. We also conduct quantitative experiments using known circuits in GPT-2; results show a strong connection between subspaces and circuit variables. We also provide evidence showing scalability to 2B models by finding separate subspaces mediating context and parametric knowledge routing. Viewed more broadly, our findings offer a new perspective on understanding model internals and building circuits.

• The paper presents the Neighbor Distance Minimization (NDM) algorithm that decomposes neural representations into orthogonal, interpretable subspaces with Gini coefficients often above 0.6.
• It employs an orthogonal transformation and iterative mutual information merging to ensure that each subspace distinctly captures mutually exclusive features.
• Empirical validation on both toy and large language models (e.g., GPT-2, 2B-scale models) demonstrates reliable alignment of subspaces with mechanistic circuits and improved interpretability.

Decomposing Neural Representation Space into Interpretable Subspaces via Unsupervised Learning

Introduction and Motivation

The paper introduces a novel unsupervised approach for decomposing the high-dimensional representation spaces of neural networks into interpretable, non-basis-aligned subspaces. The motivation is rooted in mechanistic interpretability: understanding how neural models encode and process information internally, beyond mere behavioral analysis. The central hypothesis is that neural representations, especially in LLMs, are organized such that distinct, abstract aspects of the input are encoded in approximately independent subspaces. This is motivated by the prevalence of mutual exclusivity in real-world features (e.g., a token can only be one word at a time), which, under certain conditions, should induce orthogonal subspace structure in the learned representations.

Methodology: Neighbor Distance Minimization (NDM)

The core contribution is the Neighbor Distance Minimization (NDM) algorithm, which learns an orthogonal transformation of the representation space such that the resulting subspaces are as independent as possible. The method operates as follows:

• Orthogonal Partitioning: An orthogonal matrix $\mathbf{R}$ is learned to rotate the representation space. The rotated space is then partitioned into contiguous subspaces of specified dimensions.
• Objective: For each subspace, the algorithm minimizes the average distance to the nearest neighbor (in the subspace) across a large set of activations. The intuition is that, under a correct partition, activations within a subspace will cluster tightly if they encode mutually exclusive features.
• Subspace Configuration: The number and dimensionality of subspaces are determined adaptively. Mutual information (MI) between subspaces is estimated using the KSG estimator, and subspaces with high MI are merged iteratively until all pairs are sufficiently independent.
• Optimization: The orthogonality of $\mathbf{R}$ is enforced via parameterization (e.g., using PyTorch's orthogonal matrix support), and the loss is minimized via gradient descent.

This approach is justified both by the geometry of superposition in toy models and by the information-theoretic perspective of minimizing total correlation among subspaces.

Empirical Validation in Toy Models

The method is first validated in controlled toy settings, where the ground-truth feature groups and their orthogonal structure are known. The experiments demonstrate that NDM reliably recovers the correct subspace partitioning, even when the number of features and groups is large and the dimensionality is limited. The learned orthogonal transformation aligns subspaces with the true feature groups, as evidenced by the block-diagonal structure in the transformed weight matrices.

Application to LLMs

Quantitative Evaluation

NDM is applied to the residual stream activations of GPT-2 Small and larger models (Qwen2.5-1.5B, Gemma-2-2B). The evaluation leverages known mechanistic circuits (e.g., the IOI and Greater-than circuits) and employs subspace activation patching: selectively replacing subspace activations with those from counterfactual inputs and measuring the effect on model outputs.

• Metric: The concentration of causal effect in subspaces is quantified using the Gini coefficient over patching effects. High Gini values indicate that specific information (e.g., previous token, position, subject name) is localized to a small number of subspaces.
• Results: NDM achieves Gini coefficients significantly above 0.6 (often >0.7), indicating strong concentration and interpretability, outperforming baselines such as random partitions and PCA-based subspaces.

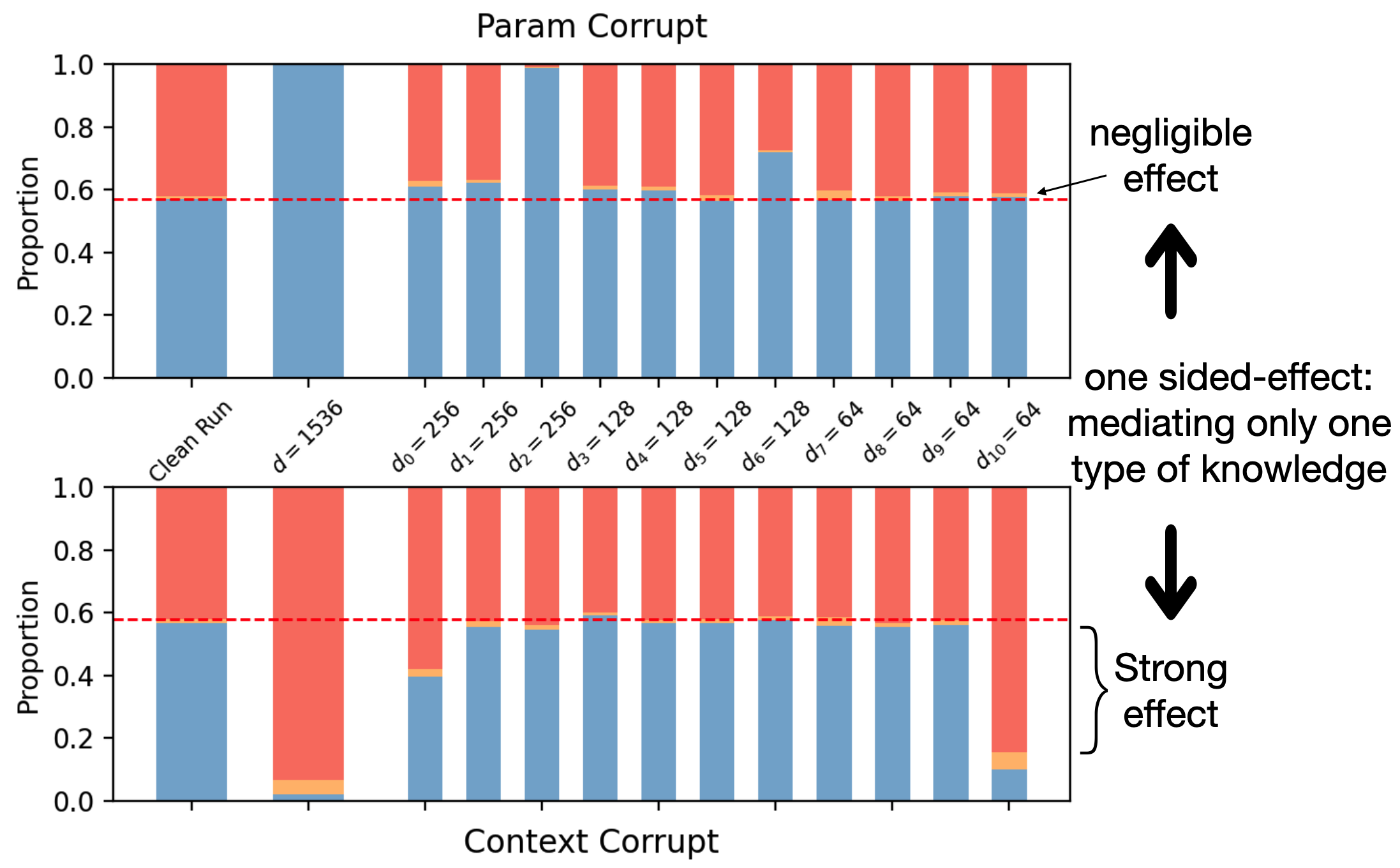
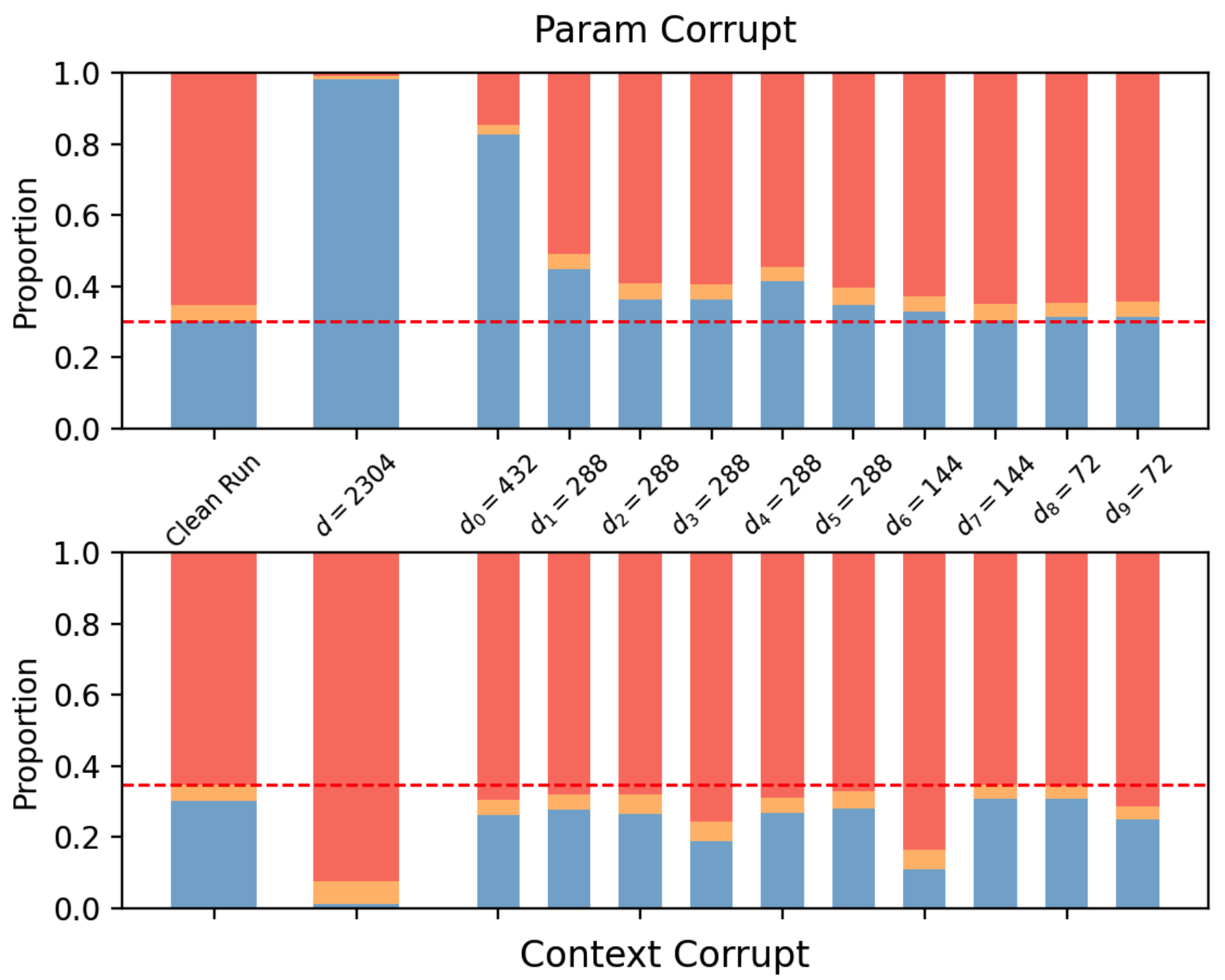
Figure 1: Subspace patching effect in Qwen2.5-1.5B and Gemma-2-2B, showing that NDM identifies subspaces mediating either parametric or context knowledge routing, with minimal cross-effect.

Qualitative Analysis

Using the InversionView method, the authors interpret subspace activations by retrieving input contexts that produce similar activations in a given subspace. This analysis reveals that:

• Different subspaces consistently encode distinct aspects of the input, such as the current token, previous token, position, or topic.
• The interpretation of a subspace is stable across inputs, supporting the hypothesis that subspaces function as "variables" in the model's computation.

  Figure 2: Clean and counterfactual inputs used in knowledge conflict experiments, illustrating how patching with activations from different sources can selectively increase the probability of context or parametric answers.

Scaling to Larger Models and Knowledge Routing

NDM is shown to scale to 2B-parameter models. In knowledge conflict experiments (e.g., when context and parametric knowledge disagree), NDM identifies subspaces that mediate either context-based or parametric knowledge routing, as demonstrated by selective patching effects. In contrast, baseline partitions do not exhibit this separation, with patching effects correlated across subspaces.

Theoretical and Practical Implications

Theoretical Implications

• Subspace Circuits: The findings support the view that neural models internally organize information into approximately independent subspaces, which can serve as the basic units for circuit analysis. This enables the construction of input-independent, weight-based circuit diagrams, potentially bridging the gap between distributed representations and symbolic computation.
• Superposition and Feature Groups: The results provide empirical support for the multi-dimensional superposition hypothesis, where mutually exclusive feature groups are encoded in orthogonal subspaces.

Practical Implications

• Interpretability: NDM provides a scalable, unsupervised tool for decomposing representation spaces, facilitating mechanistic analysis without requiring human-specified supervision or modification of model computation.
• Model Analysis and Debugging: By identifying subspaces corresponding to specific variables or mechanisms, practitioners can more effectively analyze, intervene, and potentially control model behavior.
• Scalability: The method is computationally tractable for large models, with training times on the order of hours per layer on modern hardware.

Limitations and Future Directions

• Granularity: The current merging-based approach may not recover very fine-grained (e.g., low-dimensional) subspaces, potentially missing small but important variables.
• Optimization Challenges: The orthogonal matrix optimization can get stuck in local minima, especially as dimensionality increases.
• Interpretability of All Subspaces: Not all discovered subspaces are easily interpretable; some may encode abstract or distributed control signals.
• Alternative Approaches: The paper discusses split-based and minimax (MINE-based) alternatives, but these were less effective empirically.

Future work could explore hierarchical subspace structures, more flexible dimension search, and integration with causal discovery methods. There is also potential for industry-scale application, leveraging larger datasets and compute.

Conclusion

This work demonstrates that unsupervised learning of orthogonal subspace partitions via neighbor distance minimization yields interpretable, independent subspaces in neural representation spaces. The approach is validated both in toy models and real LLMs, with strong quantitative and qualitative evidence for the interpretability and functional alignment of the discovered subspaces. The method opens new avenues for mechanistic interpretability, circuit analysis, and the development of input-independent, variable-based explanations of neural computation.