Could Living Cells Use Phase Transitions to Process Information? (2507.23384v1)

Abstract: To maintain homeostasis, living cells process information with networks of interacting molecules. Traditional models for cellular information processing have focused on networks of chemical reactions between molecules. Here, we describe how networks of physical interactions could contribute to the processing of information inside cells. In particular, we focus on the impact of biomolecular condensation, a structural phase transition found in cells. Biomolecular condensation has recently been implicated in diverse cellular processes. Some of these are essentially computational, including classification and control tasks. We place these findings in the broader context of physical computing, an emerging framework for describing how the native dynamics of nonlinear physical systems can be leveraged to perform complex computations. The synthesis of these ideas raises questions about expressivity (the range of problems that cellular phase transitions might be able to solve) and learning (how these systems could adapt and evolve to solve different problems). This emerging area of research presents diverse opportunities across molecular biophysics, soft matter, and physical computing.

• The paper proposes that phase transitions in biomolecular condensates enable living cells to process information similarly to neural network decision boundaries.
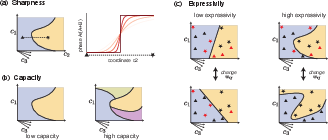
• It quantifies computational metrics such as sharpness, capacity, and expressivity, drawing parallels between phase separation and artificial computation.
• The study highlights the rapid, energy-efficient reorganization in cells through condensation, suggesting a compact mechanism for integrated sensing and control.

Phase Transitions as a Mechanism for Cellular Information Processing

Introduction

The paper "Could Living Cells Use Phase Transitions to Process Information?" (2507.23384) presents a comprehensive perspective on the role of biomolecular condensates and phase separation in cellular information processing. The authors propose that, beyond traditional chemical reaction networks, the physical interactions underlying phase transitions in multicomponent systems can endow living cells with computational capabilities such as classification and control. This framework is contextualized within the broader paradigm of physical computing, where the native dynamics of nonlinear physical systems are harnessed for computation.

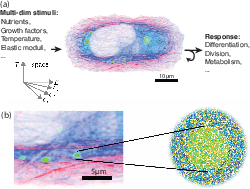
Figure 1: Living cells integrate diverse chemical and physical stimuli, potentially using biomolecular condensates such as stress granules to compute biological responses.

Biomolecular Condensates: Structure and Phase Behavior

Biomolecular condensates are non-membrane-bound compartments formed via phase separation, typically enriched in specific proteins and nucleic acids. These structures, such as stress granules, exhibit compositional diversity and are implicated in various cellular processes. The formation and dissolution of condensates are governed by the interplay of molecular interactions and entropy, which can be described by phase diagrams.

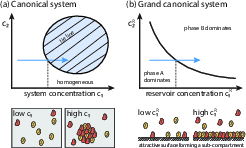
Figure 2: Phase diagrams illustrate the conditions under which biomolecular condensates form, with phase boundaries delineating transitions in component concentrations.

The canonical ensemble describes systems with conserved total material, leading to coexistence of multiple phases. In contrast, the grand canonical ensemble models compartments coupled to a reservoir, resulting in sharp phase boundaries and discontinuous transitions in composition. These physical principles underpin the ability of condensates to rapidly reorganize cellular components in response to environmental or internal cues.

Condensation as Computation: Classification and Control

The authors draw a formal analogy between phase boundaries in multicomponent systems and decision boundaries in classification tasks. In neural networks, synaptic weights $w_{ij}$ are tuned to position decision boundaries in input space. Similarly, the interaction parameters $w_{ij}$ in molecular mixtures determine the location of phase boundaries, enabling the system to map high-dimensional chemical inputs to discrete output states.

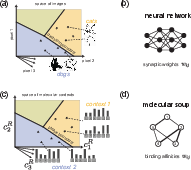
Figure 3: Phase boundaries in multicomponent systems function as decision boundaries, analogous to those in neural networks, enabling classification of molecular inputs.

This analogy extends to control tasks, where phase separation can buffer fluctuations in component concentrations, maintaining homeostasis without explicit separation of sensing, computation, and actuation. The rapid and energy-efficient reorganization afforded by condensation is exemplified in stress granule formation, transcriptional regulation, and immune cell activation.

Physical Computing vs. Modular Systems Engineering

The paper contrasts the traditional "separation of concerns" approach—where computation is modularized into sensing, processing, and actuation—with physical computing, which exploits the intrinsic dynamics of the system for computation. Physical computing solutions are compact and energy-efficient, as the input signal often drives the computation directly. However, these solutions are inherently tied to the physics of the system and lack the portability of abstract, modular designs.

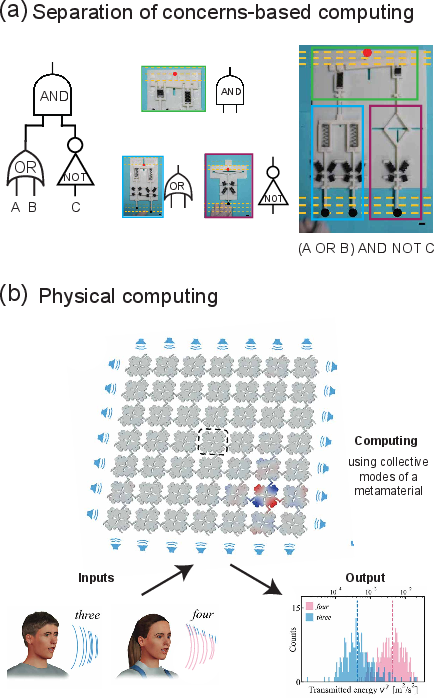
Figure 4: Comparison of modular logic gate-based computation with physical computing approaches that leverage the native dynamics of mechanical or molecular systems.

Quantifying Computational Capabilities of Phase Separation

The authors introduce metrics to assess the computational power of phase-separating systems:

• Sharpness: The maximal slope of the response across a phase boundary, determining the precision of decision-making.
• Capacity: The number of distinct phases (output categories) supported by the system.
• Expressivity: The ability to classify diverse input patterns by tuning interaction parameters.

  Figure 5: Computational metrics for phase diagrams—sharpness, capacity, and expressivity—quantify the ability of phase-separating systems to solve classification tasks.

These metrics parallel those used in neural network theory, such as VC dimension and attractor capacity. The paper highlights that hidden molecular components can function analogously to hidden neurons, enhancing expressivity by modulating effective interactions. Furthermore, kinetic phenomena such as nucleation and competitive growth can sharpen decision boundaries and increase expressivity beyond equilibrium limits.

Physical Determinants and Learning Mechanisms

The computational abilities of condensates are shaped by both equilibrium and non-equilibrium dynamics. Kinetic competition, resource depletion, and active processes (e.g., ATP-driven reactions) can enhance sharpness and control. Temporal information processing is enabled by transient phenomena such as Ostwald ripening and nucleation delays, which are exploited in biological contexts like DNA damage response and T cell activation.

The paper speculates on mechanisms for learning in condensate-based systems. Post-translational modifications and regulation of hidden component expression can reconfigure phase behavior, enabling adaptation without genetic changes. Hebbian-like updates may arise if phase separation influences the expression of scaffolding proteins, providing a route to local, non-genetic learning.

Implications and Future Directions

The perspective advanced in this paper has significant implications for both theoretical and experimental research. It suggests that phase separation offers a compact, efficient, and robust mechanism for cellular computation, integrating sensing, processing, and actuation. This challenges the prevailing modular view in systems biology and opens new avenues for understanding the computational capabilities of living matter.

Future work will require the development of tractable model systems, precise control of input and output signals, and systematic exploration of the physical determinants of computational metrics. Theoretical advances will be needed to relate kinetic and active processes to expressivity, capacity, and sharpness in multicomponent systems.

Conclusion

This paper articulates a formal framework for understanding phase separation as a mechanism for information processing in living cells. By leveraging the physics of biomolecular condensates, cells may achieve classification, control, and learning in a manner analogous to artificial neural networks, but with distinct advantages in efficiency and integration. The synthesis of physical computing and molecular biophysics promises to deepen our understanding of cellular regulation and inspire novel approaches in synthetic biology and active matter research.