Physics-informed, boundary-constrained Gaussian process regression for the reconstruction of fluid flow fields (2507.17582v1)

Abstract: Gaussian process regression techniques have been used in fluid mechanics for the reconstruction of flow fields from a reduction-of-dimension perspective. A main ingredient in this setting is the construction of adapted covariance functions, or kernels, to obtain such estimates. In this paper, we derive physics-informed kernels for simulating two-dimensional velocity fields of an incompressible (divergence-free) flow around aerodynamic profiles. These kernels allow to define Gaussian process priors satisfying the incompressibility condition and the prescribed boundary conditions along the profile in a continuous manner. Such physical and boundary constraints can be applied to any pre-defined scalar kernel in the proposed methodology, which is very general and can be implemented with high flexibility for a broad range of engineering applications. Its relevance and performances are illustrated by numerical simulations of flows around a cylinder and a NACA 0412 airfoil profile, for which no observation at the boundary is needed at all.

• The paper presents a novel method using spectral projection to construct divergence-free GP priors that enforce slip boundary conditions without explicit data on the boundary.
• It validates the approach by accurately reconstructing velocity fields around cylinders and airfoils, demonstrating effectiveness at Reynolds numbers of 3×10³ and 2.7×10³ respectively.
• The framework offers a meshfree and flexible solution that improves accuracy and reduces computational cost compared to traditional discrete constraint methods.

Physics-Informed, Boundary-Constrained Gaussian Process Regression for Fluid Flow Field Reconstruction

Introduction and Motivation

The paper presents a rigorous framework for reconstructing two-dimensional incompressible fluid flow fields around aerodynamic profiles using Gaussian Process Regression (GPR) with physics-informed, boundary-constrained kernels. The approach addresses the challenge of enforcing both incompressibility and slip boundary conditions in a continuous manner, without requiring explicit observations on the profile boundary. This is achieved by constructing Gaussian process (GP) priors that are divergence-free and satisfy homogeneous Dirichlet conditions on arbitrary compact sets, leveraging a spectral projection methodology. The resulting framework is meshfree, geometrically flexible, and suitable for data assimilation in fluid dynamics, particularly in scenarios with limited or heterogeneous data.

Mathematical Framework

Gaussian Process Regression and Constraints

The foundation of the method is the classical GPR framework, where a scalar-valued GP $Z(\mathbf{x}) \sim (0, G)$ is defined over a domain $\Omega \subset \mathbb{R}^d$ with covariance kernel $G$. Standard GPR provides closed-form expressions for the posterior mean and covariance given observations, and can be extended to include derivative information via linear operators.

To enforce continuous constraints (e.g., boundary conditions), the paper employs a spectral approach based on the Karhunen-Loève expansion. For a compact set $\Gamma \subset \Omega$, the GP is projected such that the resulting process vanishes on $\Gamma$ (homogeneous Dirichlet condition). The constrained kernel is constructed as

$$K_0(\mathbf{x}, \mathbf{x}') = G(\mathbf{x}, \mathbf{x}') - \sum_{n=0}^{\infty} \lambda_n \phi_n^*(\mathbf{x}) \phi_n^*(\mathbf{x}'),$$

where $(\lambda_n, \phi_n)$ are the eigenpairs of the integral operator associated with $G$ restricted to $\Gamma$, and $\phi_n^*$ are their liftings to $\Omega$. This construction ensures that the GP sample paths satisfy the constraint everywhere on $\Gamma$.

Parameterized and Manifold Boundaries

The method generalizes to parameterized compact manifolds, such as the boundaries of cylinders or airfoils, by appropriately choosing the measure in the spectral expansion (e.g., uniform or surface measure). The eigenproblem is discretized using Nyström quadrature, and the kernel is approximated by truncating the spectral series, with convergence controlled by a spectral accuracy threshold.

Computational Considerations

The computational bottleneck is the offline construction of the constrained kernel, which involves solving a generalized eigenvalue problem. However, this cost is amortized over multiple GPR queries, and the online complexity is dominated by Gram matrix inversion, scaling as $\mathcal{O}(N^3)$ for $N$ observations. The method is more efficient than enforcing constraints via discrete collocation points, which increases the Gram matrix size and computational cost.

Physics-Informed Kernels for Incompressible Flows

Divergence-Free and Boundary-Constrained Priors

For incompressible 2D flows, the velocity field $\mathbf{u}$ is modeled as the curl of a scalar stream function $\psi$, i.e., $\mathbf{u} = \nabla^\perp \psi$. By modeling $\psi$ as a boundary-constrained GP, the resulting velocity field is divergence-free by construction and satisfies the slip boundary condition on the profile boundary. The covariance of the velocity field is obtained by applying differential operators to the constrained kernel:

$$K_{\mathbf{u}}(\mathbf{x}, \mathbf{x}') = \nabla^\perp \otimes \nabla^{\perp'} K_0(\mathbf{x}, \mathbf{x}').$$

GPR Observation Design

The GPR framework accommodates observations of velocity at arbitrary locations, including domain boundaries and the interior, without requiring data on the profile boundary. The posterior mean provides an estimate of the velocity field that is physically consistent everywhere. The method also enables direct reconstruction of derived quantities such as vorticity and the stream function.

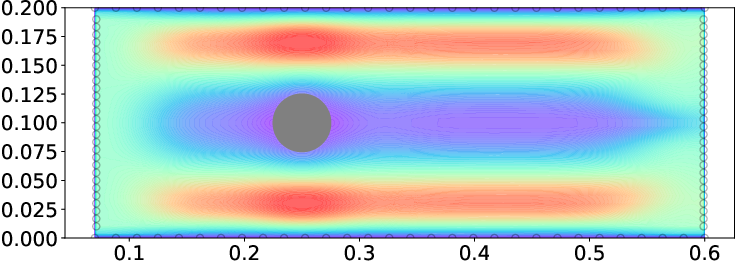
Figure 2: Schematic of the computational domain and GPR observation design, illustrating boundary, inlet/outlet, and interior observation points, with no points on the profile boundary.

Numerical Implementation and Algorithmic Details

Spectral Discretization and Kernel Evaluation

The constrained kernel is computed by discretizing the profile boundary and solving the associated eigenproblem. The number of spectral modes is chosen to meet a prescribed accuracy, and the kernel and its derivatives are evaluated using the truncated expansion. The method supports both uniform and surface measures for the spectral expansion, ensuring flexibility for arbitrary geometries.

Derivatives and Regularity

The approach supports computation of kernel derivatives up to the regularity of the base kernel, enabling the evaluation of velocity and vorticity fields. The derivatives are computed analytically from the spectral expansion, without requiring derivatives of the eigenfunctions themselves.

Empirical Results: Flow Around Cylinder and Airfoil

Cylinder Profile

The method is validated on the reconstruction of flow around a cylinder at $Re = 3 \times 10^3$, using ground-truth data from OpenFOAM. The BCGP-based GPR achieves accurate reconstruction of the velocity field, enforcing the slip boundary condition continuously without any observations on the profile boundary.

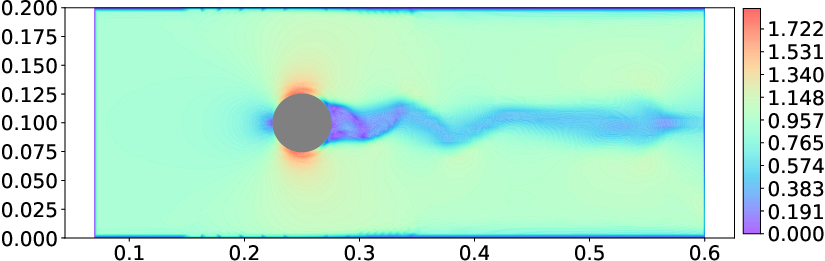
Figure 4: Ground truth velocity field of an incompressible fluid flow around a cylinder profile in a wind-tunnel setting.

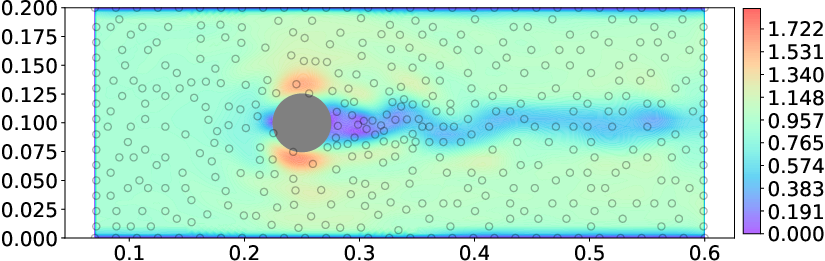
Figure 3: Physics-informed GPR reconstruction of the velocity field around a cylinder using 415 observations, with no design points on the profile boundary.

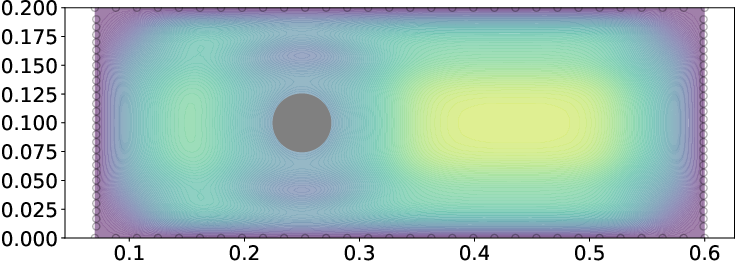
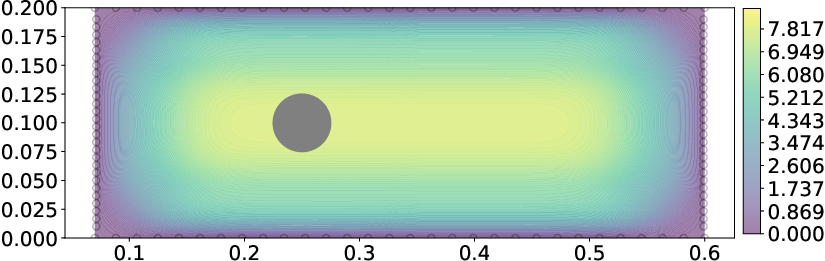
Figure 1: Total standard deviation of the velocity field reconstructed by GPR with (left) and without (right) BCGP kernels, showing reduced uncertainty near the profile boundary when using BCGP.

A convergence paper demonstrates that the spectral truncation achieves high accuracy in enforcing the boundary condition, with the $L^1$ norm of the stream function on the profile boundary reaching $10^{-7}$ for a spectral accuracy bound of $10^{-12}$.

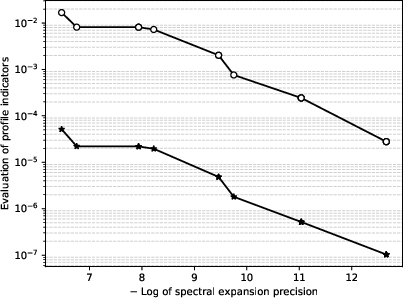
Figure 6: Convergence of physical constraint indicators on the profile boundary with respect to spectral expansion accuracy.

Comparison with a discrete constraint approach (enforcing the slip condition at collocation points) shows that the BCGP method achieves superior enforcement of the boundary condition and lower relative error for the same observation budget.

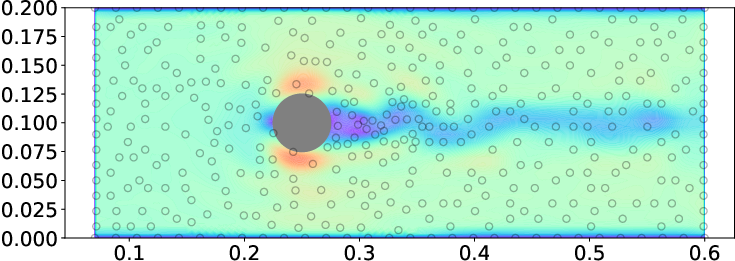
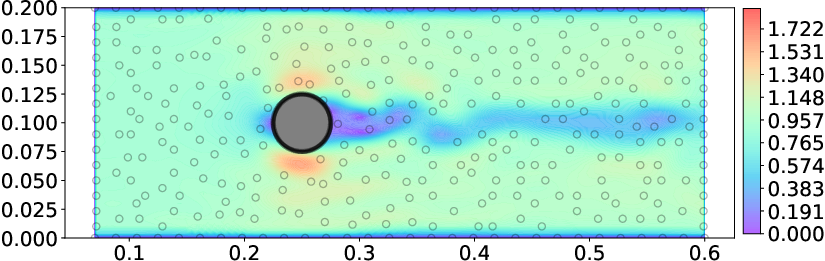
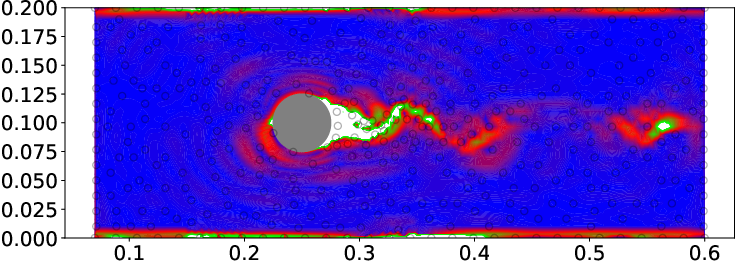
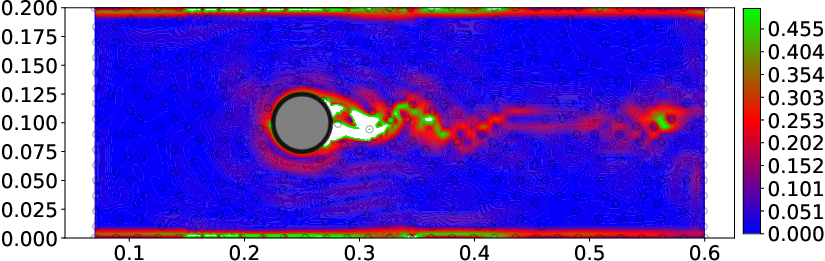
Figure 5: Velocity and relative error fields for BCGP (left) and discrete constraint (right) approaches, with observation points indicated.

NACA 0412 Airfoil

The method is further validated on flow around a NACA 0412 airfoil at $Re = 2.7 \times 10^3$, using high-fidelity data from the AirfRANS dataset. An additive anisotropic Gaussian kernel is used to capture multi-scale flow features. The BCGP-based GPR achieves accurate reconstruction of the velocity field, with the slip boundary condition enforced continuously.

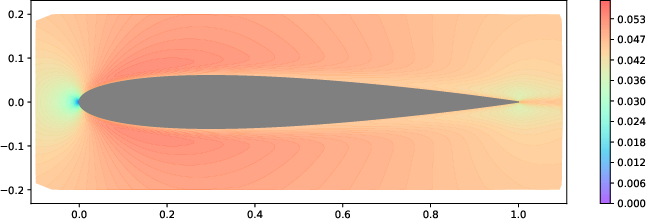
Figure 7: Ground truth velocity field of an incompressible fluid flow around the NACA 0412 airfoil.

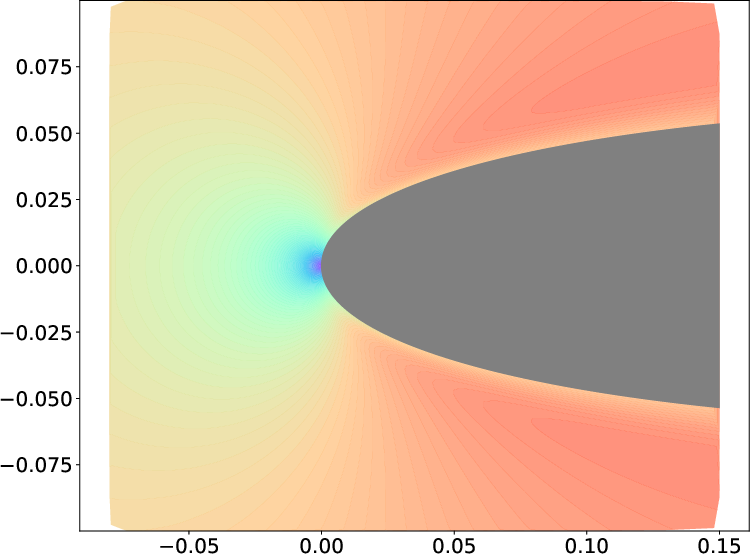
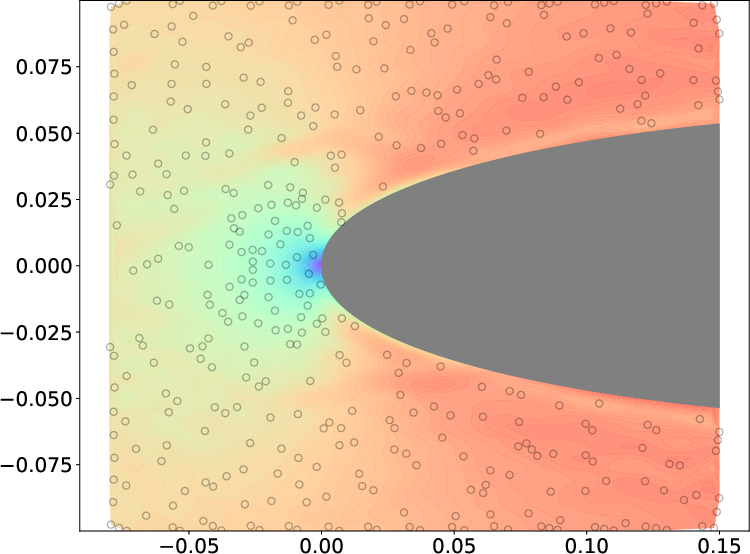
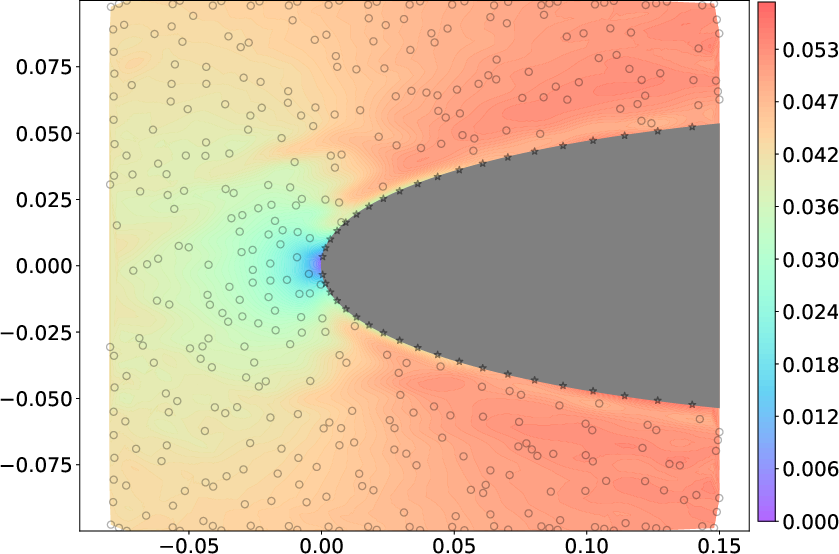
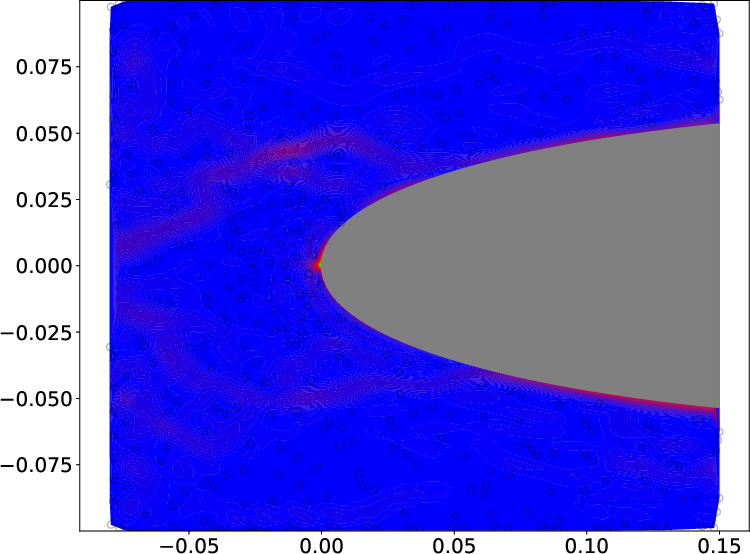
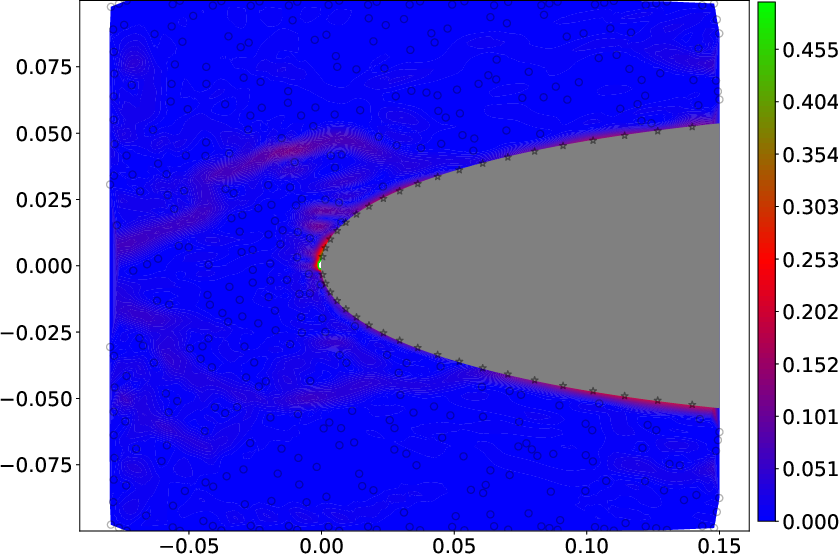
Figure 8: GPR velocity field estimates for the NACA 0412 airfoil: (a) ground truth, (b) BCGP-based, (c) discrete constraint, and (d,e) corresponding relative error fields.

A convergence paper confirms that the BCGP approach achieves comparable or better enforcement of the boundary condition compared to the discrete approach, without requiring any profile boundary observations.

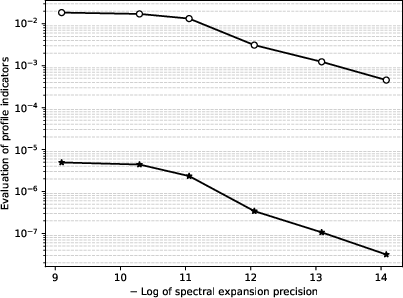
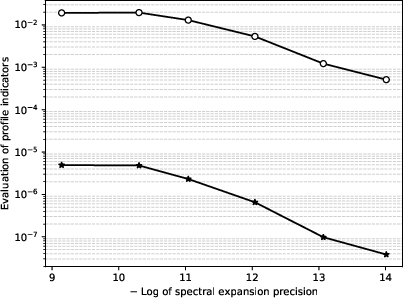
Figure 9: Convergence of physical constraint indicators for the NACA 0412 airfoil with respect to spectral expansion accuracy, for both pushforward and surface measures.

Discussion and Implications

The proposed framework provides a principled and efficient method for reconstructing incompressible flow fields with strong physical guarantees. By enforcing constraints in the prior, the method avoids the need for collocation points on the profile boundary, allowing the observation budget to be allocated to more informative locations. The spectral approach is general and can be applied to arbitrary geometries and base kernels, supporting a wide range of engineering applications.

The method is particularly advantageous in data-scarce regimes and for data assimilation tasks, as it enables the integration of heterogeneous data sources while maintaining physical consistency. The meshfree nature and flexibility in kernel design make it suitable for integration with Lagrangian particle methods and for extension to more complex physical constraints.

Potential future developments include the use of sparse GP approximations to improve scalability, adaptive experimental design for optimal observation placement, and joint inference of multiple physical quantities (e.g., velocity, vorticity, pressure). The framework is also amenable to integration with operator learning and foundation models for PDEs, providing a bridge between kernel methods and modern deep learning approaches.

Conclusion

The paper establishes a robust methodology for physics-informed, boundary-constrained GPR in fluid dynamics, enabling accurate and physically consistent reconstruction of incompressible flow fields around complex profiles. The spectral construction of constrained kernels ensures continuous enforcement of boundary conditions, outperforming discrete constraint methods in both accuracy and computational efficiency. The approach is broadly applicable, scalable, and provides a foundation for further advances in physics-informed machine learning for scientific computing.