AutoHFormer: Efficient Hierarchical Autoregressive Transformer for Time Series Prediction (2506.16001v1)

Abstract: Time series forecasting requires architectures that simultaneously achieve three competing objectives: (1) strict temporal causality for reliable predictions, (2) sub-quadratic complexity for practical scalability, and (3) multi-scale pattern recognition for accurate long-horizon forecasting. We introduce AutoHFormer, a hierarchical autoregressive transformer that addresses these challenges through three key innovations: 1) Hierarchical Temporal Modeling: Our architecture decomposes predictions into segment-level blocks processed in parallel, followed by intra-segment sequential refinement. This dual-scale approach maintains temporal coherence while enabling efficient computation. 2) Dynamic Windowed Attention: The attention mechanism employs learnable causal windows with exponential decay, reducing complexity while preserving precise temporal relationships. This design avoids both the anti-causal violations of standard transformers and the sequential bottlenecks of RNN hybrids. 3) Adaptive Temporal Encoding: a novel position encoding system is adopted to capture time patterns at multiple scales. It combines fixed oscillating patterns for short-term variations with learnable decay rates for long-term trends. Comprehensive experiments demonstrate that AutoHFormer 10.76X faster training and 6.06X memory reduction compared to PatchTST on PEMS08, while maintaining consistent accuracy across 96-720 step horizons in most of cases. These breakthroughs establish new benchmarks for efficient and precise time series modeling. Implementations of our method and all baselines in hierarchical autoregressive mechanism are available at https://github.com/lizzyhku/Autotime.

• The paper introduces AutoHFormer, a novel hierarchical autoregressive transformer that integrates dynamic windowed attention and adaptive temporal encoding for efficient time series prediction.
• It demonstrates sub-quadratic computational complexity with up to 10.76× faster training and significant memory reductions on diverse real-world datasets.
• The method ensures temporal causality and robust multi-scale pattern recognition, validated by theoretical guarantees and comprehensive experimental results.

Efficient Hierarchical Autoregressive Transformer for Time Series Prediction

The paper introduces AutoHFormer, a novel hierarchical autoregressive transformer architecture designed for efficient and accurate time series prediction (2506.16001). This architecture addresses the challenges of simultaneously achieving temporal causality, sub-quadratic complexity, and multi-scale pattern recognition. AutoHFormer employs a hierarchical temporal modeling approach, dynamic windowed attention, and adaptive temporal encoding to overcome limitations in existing time series forecasting models.

Addressing Limitations of Existing Approaches

Traditional Transformer architectures suffer from anti-causal attention flows, violating the principle of temporal causality (Figure 1). RNN-Transformer hybrids enforce causality through sequential processing but introduce computational bottlenecks. AutoHFormer addresses these limitations by combining causal attention within a sliding window, exponentially decaying attention weights, and $\mathcal{O}(LW)$ complexity through windowed parallel processing. This approach maintains temporal causality while enabling efficient parallel computation.

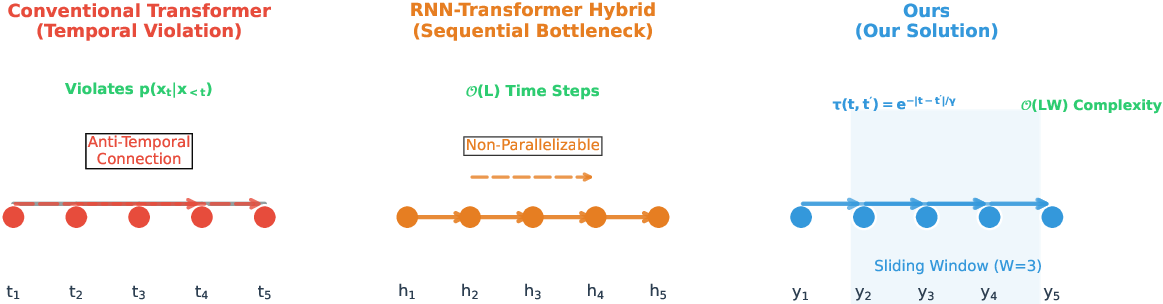
Figure 1: Architectural comparison of time series modeling approaches, highlighting how AutoHFormer maintains temporal causality with efficient parallel computation.

AutoHFormer Architecture and Innovations

The AutoHFormer architecture (Figure 2) comprises three key innovations:

1. Hierarchical Temporal Modeling: The architecture decomposes predictions into segment-level blocks processed in parallel, followed by intra-segment sequential refinement. This dual-scale approach maintains temporal coherence while enabling efficient computation. Layer-normalized residual updating and moving average smoothing are proposed to enable stable prediction within segments.
2. Dynamic Windowed Attention: The attention mechanism employs learnable causal windows with exponential decay, reducing complexity while preserving temporal relationships. The window size $W$ acts as a hyperparameter controlling the trade-off between context range and efficiency. The trainable parameter $\gamma$ automatically adapts to dataset characteristics.
3. Adaptive Temporal Encoding: A novel position encoding system is adopted to capture time patterns at multiple scales. It combines fixed oscillating patterns for short-term variations with learnable decay rates for long-term trends.

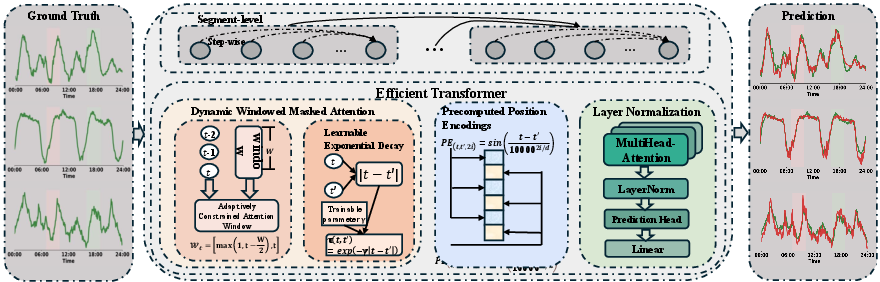
   Figure 2: An overview of the AutoHFormer architecture, showcasing its hierarchical autoregressive mechanism, dynamic windowed attention, and adaptive temporal encoding.

Implementation Details

Dynamic Windowed Masked Attention (DWMA)

The DWMA mechanism employs adaptively constrained attention windows defined as $$\mathcal{W}_t = \left[\max\left(1, t-\frac{W}{2}\right), t\right]$$, establishing dynamic receptive fields that maintain strict causality while enabling $\mathcal{O}(LW)$ computational complexity. Position-sensitive weighting is introduced via $\tau(t,t') = \exp\left(-\gamma|t-t'|\right)$, where the trainable parameter $\gamma$ automatically adapts to dataset characteristics.

Precomputed Position Encodings (PPE)

PPE explicitly encode the relative positions of all pairs of time steps $(t, t')$ using sinusoidal functions. The encoding for dimension $i$ is defined as: $PE_{(t, t', 2i)} = \sin\left(\frac{t - t'}{10000^{2i/d}\right)$, $PE_{(t, t', 2i+1)} = \cos\left(\frac{t - t'}{10000^{2i/d}\right)$.

These encodings are precomputed and stored in a lookup table $\mathbf{PE} \in \mathbb{R}^{L \times L \times d}$, avoiding redundant computations during training and inference. During the attention computation, the relative position encodings $\mathbf{PE}_{t, t'}$ are added to the query-key dot product: $A_{t,t'} = \text{softmax}\left(\frac{Q_t(K_{t'} + \mathbf{PE}_{t,t'})^\top \cdot \tau_{\text{time}(t,t')}{\sqrt{d_k}\right)$, where $\tau(t,t') = \exp(-\gamma|t-t'|)$ implements the learnable decay kernel.

Experimental Results

Comprehensive experiments on benchmark datasets demonstrate the superior performance of AutoHFormer compared to state-of-the-art baselines. AutoHFormer achieves 10.76$\times$ faster training and 6.06$\times$ memory reduction compared to PatchTST on PEMS08, while maintaining consistent accuracy across 96-720 step horizons in most cases. Table 2 presents comprehensive results of AutoHFormer and baselines on various datasets in the autoregressive setting. The lookback length $L$ is fixed at 336, and the forecast length $T$ varies across 96, 192, 336, and 720. AutoHFormer consistently ranks among the top performers in most evaluations across six diverse real-world datasets.

Scalability Study

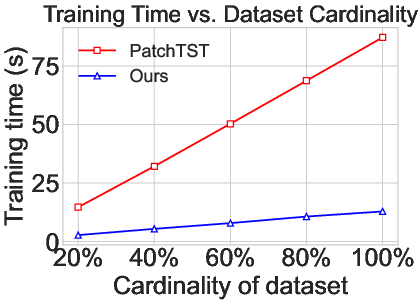
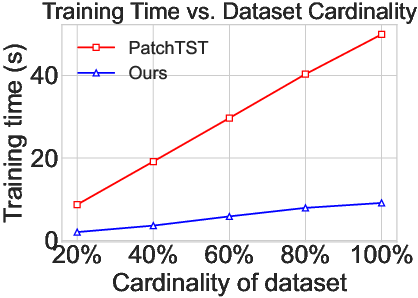
Figure 3: A scalability paper demonstrating the training time of PatchTST and AutoHFormer on PEMS04 and PEMS08 datasets with varying cardinalities.

The scalability of AutoHFormer is evaluated in terms of training data size (Figure 3). The results demonstrate that AutoHFormer maintains lower training times compared to PatchTST as dataset cardinality increases from 20% to 100%. This indicates that AutoHFormer's architectural innovations effectively address scalability limitations present in conventional approaches.

Case Study

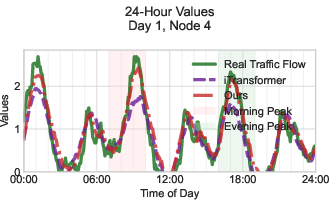
Figure 4: Case paper of AutoHFormer and iTransformer on ETTm1 in terms of temporal patterns and short transients.

A case paper comparing AutoHFormer and iTransformer on the ETTm1 dataset (Figure 4) reveals that AutoHFormer demonstrates superior alignment with ground truth measurements, achieving more accurate peak magnitude variations, precise temporal alignment of traffic surges, and accurate capture of both short transients and daily periodicity.

Theoretical Guarantees

The paper provides theoretical guarantees for the proposed method, ensuring its effectiveness in capturing temporal dependencies and causal relationships in time series data.

Theorem 1: The Dynamic Windowed Masked Attention (DWMA) mechanism converges to an optimal attention distribution as the sequence length $L \to \infty$, provided the time decay factor $\gamma$ is chosen appropriately.

Theorem 2: The Precomputed Position Encodings (PPE) reduce the computational complexity of positional encoding from $\mathcal{O}(L^2 \cdot d)$ to $\mathcal{O}(L \cdot d)$ during inference.

Conclusion

AutoHFormer introduces a hierarchical autoregressive transformer that advances time series forecasting by addressing the challenges of causality, efficiency, and multi-scale pattern recognition. The architecture's innovations, including hierarchical processing, dynamic windowed attention, and hybrid temporal encodings, enable it to outperform existing approaches in terms of training speed, memory reduction, and prediction accuracy. The theoretical guarantees and comprehensive experimental results validate AutoHFormer as a promising solution for industrial applications requiring both efficiency and precision.