Opinion dynamics on biased dynamical networks: beyond rare opinion updating (2404.02913v1)

Abstract: Opinion dynamics is of paramount importance as it provides insights into the complex dynamics of opinion propagation and social relationship adjustment. It is assumed in most of the previous works that social relationships evolve much faster than opinions. This is not always true in reality. We propose an analytical approximation to study this issue for arbitrary time scales between opinion adjustment and network evolution. To this end, the coefficient of determination in statistics is introduced and a one-dimensional stable manifold is analytically found, i.e., the most likely trajectory. With the aid of the stable manifold, we further obtain the fate of opinions and the consensus time, i.e., fixation probability and fixation time. We find that for in-group bias, the more likely individuals are to adopt the popular opinion, the less likely the majority opinion takes over the population, i.e., conformity inhibits the domination of popular opinions. This counter-intuitive result can be interpreted from a game perspective, in which in-group bias refers to a coordination game and rewiring probability refers to a rescaling of the selection intensity. Our work proposes an efficient approximation method to foster the understanding of opinion dynamics in dynamical networks.

• The paper presents an analytical framework that allows arbitrary time scales between opinion updating and social network evolution, establishing a one-dimensional stable manifold for consensus prediction.
• It demonstrates that when opinion dynamics are balanced, the fixation probability is linearly proportional to the initial opinion share and independent of update speed.
• It shows that in-group and out-group biases can skew the expected diffusion, with conformity sometimes counterintuitively hindering majoritarian dominance.

Opinion Dynamics on Biased Dynamical Networks

Introduction

The paper "Opinion dynamics on biased dynamical networks: beyond rare opinion updating" investigates the co-evolution of opinions and social relationships on networks, proposing an analytical framework to explore the interplay between opinion propagation and dynamic network structures. Previous models often assume rapid social relationship adjustments compared to opinion changes, which oversimplifies some real-world dynamics. This work offers an analytical approach allowing for arbitrary time scales between opinion and network evolution, providing a broader understanding of how opinions stabilize or shift over time in social networks.

Stable Manifold and Opinion Dynamics

The authors introduce a one-dimensional stable manifold as a theoretical construct within which the network dynamics aligns, irrespective of initial conditions. This manifold represents the most probable trajectory towards consensus, described by the variables $u$, $v$, and $w$, which capture the proportions of homogeneous edges and the imbalance between two competing opinions. The stability of this manifold (Figure 1) implies that under diverse initial conditions, the system will consistently converge to a specific trajectory encapsulated within this stable manifold. This convergence results in a predictable diffusion process on a one-dimensional Markov chain, effectively capturing the essence of opinion dynamics on these networks.

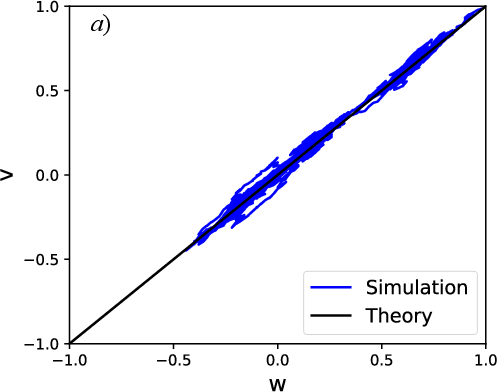
Figure 1: The system converges to the stable manifold and takes a random walk on it. (a) $v$ and (b) $u$ as functions of $w$, i.e., the stable manifold.

Fixation Probability and Time

In the benchmark scenario where an opinion has equal dynamics (i.e., $k_d = k_s$), the probability of opinion fixation becomes a simple function of its initial proportion, ensuring that the likelihood of an opinion taking over is linearly proportional to its initial presence (Figure 2). This leads to a fixation probability independent of the time scale of opinion updates, highlighting the robustness of opinion dynamics against variations in social and opinion adjustment speeds.

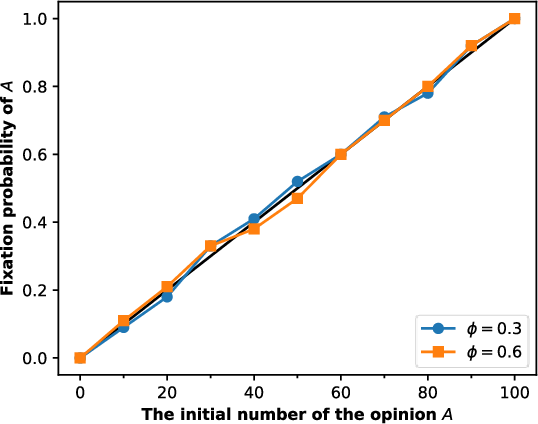
Figure 2: The fixation probability is independent of $\phi$ for $k_d=k_s$.

For real-world applications where $k_d \neq k_s$, corresponding to in-group or out-group biases, the paper provides derived estimates of fixation probabilities and times, using a modified manifold that incorporates these biases. As expected, the presence of in-group or out-group biases skews the trajectory. Conformity, represented by $\phi$, interestingly discourages majoritarian dominance in in-group biased networks, revealing an unintuitive dynamic where conformity can act against the prevailing majority (Figure 3).

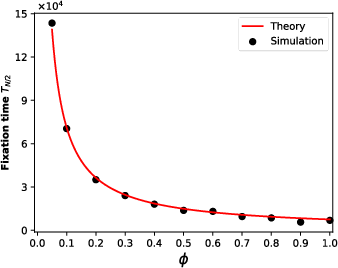
Figure 3: Simulation results coincide perfectly with the theoretical results.

Theoretical Implications

The research expands the understanding of how dynamically co-evolving social structures and individual opinions influence the path towards consensus. The stable manifold concept serves as a predictive tool to model real-world sociological phenomena where opinions do not change in isolation but alongside evolving social connections. This coupling between social awareness and opinion dynamics is crucial for analyzing scenarios such as political campaigns, marketing strategies, or social movements where peer influence and network restructuring play significant roles.

Conclusion

The work is a theoretical advancement in modeling opinion dynamics on dynamical networks, providing analytical methods to predict opinion convergence and annihilation under varied conditions. It highlights novel phenomena where biases disrupt intuitive dynamics, thus offering insights critical for policy-making, understand strategic opinion interventions, and optimize information dissemination in socio-cultural contexts. Future research can leverage this foundation to tackle multi-dimensional opinion models, enriching the field's predictive capabilities and operational applications.