The Forward-Forward Algorithm: Some Preliminary Investigations (2212.13345v1)

Abstract: The aim of this paper is to introduce a new learning procedure for neural networks and to demonstrate that it works well enough on a few small problems to be worth further investigation. The Forward-Forward algorithm replaces the forward and backward passes of backpropagation by two forward passes, one with positive (i.e. real) data and the other with negative data which could be generated by the network itself. Each layer has its own objective function which is simply to have high goodness for positive data and low goodness for negative data. The sum of the squared activities in a layer can be used as the goodness but there are many other possibilities, including minus the sum of the squared activities. If the positive and negative passes could be separated in time, the negative passes could be done offline, which would make the learning much simpler in the positive pass and allow video to be pipelined through the network without ever storing activities or stopping to propagate derivatives.

• The paper introduces the Forward-Forward algorithm that replaces backpropagation with two forward passes for processing real and negative data.
• It employs a greedy, layer-wise approach with goodness criteria, enhancing differentiation between positive and negative data.
• Experimental results on MNIST and CIFAR-10 illustrate the method's potential for real-time, energy-efficient learning.

Introduction

The paper "The Forward-Forward Algorithm: Some Preliminary Investigations" (2212.13345) introduces a novel learning mechanism for neural networks that deviates significantly from traditional backpropagation. Known as the Forward-Forward (FF) Algorithm, it advocates for replacing the forward and backward passes of backpropagation with two forward passes, one involving real data (positive pass) and the other using negative data that may be internally generated by the network itself.

Limitations of Backpropagation

The paper underscores several limitations inherent in backpropagation, especially regarding its biological plausibility. Backpropagation demands precise knowledge of the computation occurring in the forward pass, which is often unattainable in real-world neuron situations. Moreover, if any unknown or non-linear element—a "black box"—is integrated into the forward pass, the backpropagation becomes infeasible without modeling this intermediary. This contrasts sharply with FF, which remains unaffected by unknown non-linearities.

Additionally, backpropagation is impractical for handling sequential data, which necessitates real-time learning without the interruption of backward passes. FF, on the other hand, facilitates continuous data pipelining and can operate without storing intermediate neural activities or derivatives.

The Forward-Forward Algorithm

The FF algorithm proposes a greedy, layer-wise approach inspired by Boltzmann machines and Noise Contrastive Estimation (NCE). Each layer strives for higher "goodness" with positive data and lower goodness with negative data. This creates a robust mechanism for differentiating data classes without traditional error propagation.

Goodness Criteria

The paper examines various measures for "goodness," primarily focusing on the sum of squared activities (positive orientation measure). An alternative is the negative sum of squared activities (negative orientation measure), with potential to yield varied insights.

Layer-wise Learning

FF utilizes layer normalization, enhancing the network's ability to capture relative neuron activities while preserving critical vector lengths, which are inherently used in determining layer goodness.

Experimentation and Results

FF is validated across diverse tests on neural networks handling small datasets. Its performance, in comparison to backpropagation, highlights FF's potential for efficiently utilizing low-power analog hardware while modeling learning processes in neural cortex.

Figure 1: A hybrid image used as negative data.

Unsupervised Learning

For unsupervised tasks, FF was tested on MNIST, applying negative data from cleverly corrupted input representations demonstrating varying correlation patterns. FF effectively reduced test error rates comparable to standard methods, with additional improvements seen through local receptive fields.

Figure 2: The receptive fields of 100 neurons in the first hidden layer of the network trained on jittered MNIST. The class labels are represented in the first 10 pixels of each image.

CIFAR-10 Tests

FF was compared with backpropagation on CIFAR-10 data, illustrating competitive performance despite complex environmental backgrounds, by exploiting local receptive fields and iterative evaluations.

Implications and Future Prospects

The FF algorithm holds promise in simplifying the training processes for AI models, particularly in contexts requiring real-time computation or energy-efficient hardware implementations. Its absence of reliance on backpropagation, while still fostering effective learning, suggests potential future expansions into larger network domains, or applications where sophisticated neural modeling is pivotal.

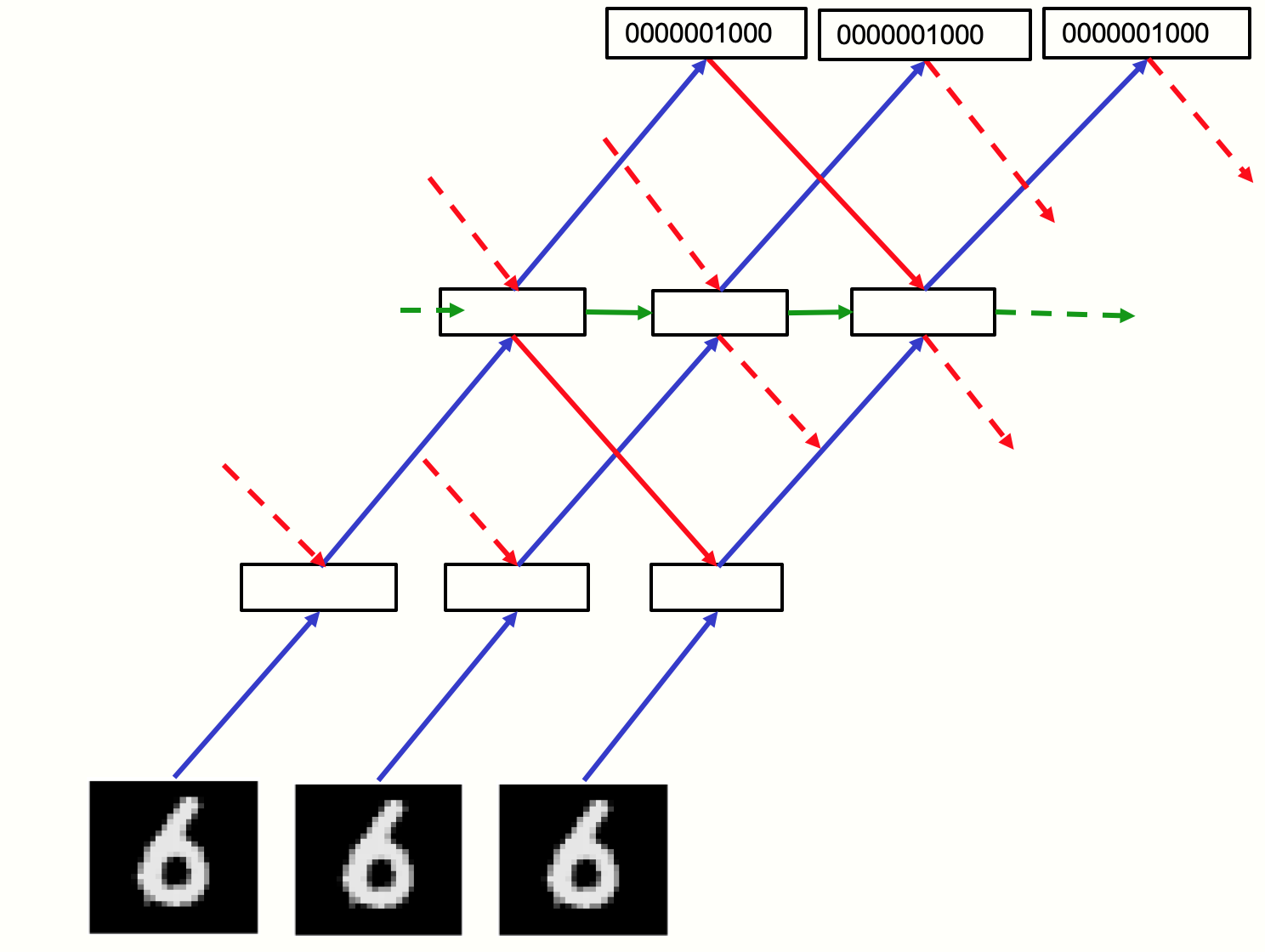
Figure 3: The recurrent network used to process video.

Conclusion

The exploration of the Forward-Forward algorithm presents a compelling alternative to backpropagation, with unique advantages in biological modeling and energy-efficient hardware implementations. Despite current limitations in generalization speed and error minimization, FF is poised for substantial relevance in future neural network advancements. This paper sets a foundational understanding ready for further research into potential scalability and practical deployment.