Recovering single precision accuracy from Tensor Cores while surpassing the FP32 theoretical peak performance
Abstract: Tensor Core is a mixed-precision matrix-matrix multiplication unit on NVIDIA GPUs with a theoretical peak performance of more than 300 TFlop/s on Ampere architectures. Tensor Cores were developed in response to the high demand of dense matrix multiplication from machine learning. However, many applications in scientific computing such as preconditioners for iterative solvers and low-precision Fourier transforms can exploit these Tensor Cores. To compute a matrix multiplication on Tensor Cores, we need to convert input matrices to half-precision, which results in loss of accuracy. To avoid this, we can keep the mantissa loss in the conversion using additional half-precision variables and use them for correcting the accuracy of matrix-matrix multiplication. Even with this correction, the use of Tensor Cores yields higher throughput compared to FP32 SIMT Cores. Nevertheless, the correcting capability of this method alone is limited, and the resulting accuracy cannot match that of a matrix multiplication on FP32 SIMT Cores. We address this problem and develop a high accuracy, high performance, and low power consumption matrix-matrix multiplication implementation using Tensor Cores, which exactly matches the accuracy of FP32 SIMT Cores while achieving superior throughput. The implementation is based on NVIDIA's CUTLASS. We found that the key to achieving this accuracy is how to deal with the rounding inside Tensor Cores and underflow probability during the correction computation. Our implementation achieves 51TFlop/s for a limited exponent range using FP16 Tensor Cores and 33TFlop/s for full exponent range of FP32 using TF32 Tensor Cores on NVIDIA A100 GPUs, which outperforms the theoretical FP32 SIMT Core peak performance of 19.5TFlop/s.
- Mixed Precision Block Fused Multiply-Add: Error Analysis and Application to GPU Tensor Cores. SIAM Journal on Scientific Computing, 42(3):C124–C141, January 2020. Publisher: Society for Industrial and Applied Mathematics.
- Quantum Accelerators for High-Performance Computing Systems. 2017 IEEE International Conference on Rebooting Computing (ICRC), pages 1–7, November 2017. arXiv: 1712.01423.
- Analyzing GPU Tensor Core Potential for Fast Reductions. In 2018 37th International Conference of the Chilean Computer Science Society (SCCC), pages 1–6, November 2018. ISSN: 1522-4902.
- Accelerating the Solution of Linear Systems by Iterative Refinement in Three Precisions. SIAM Journal on Scientific Computing, 40(2):A817–A847, January 2018. Publisher: Society for Industrial and Applied Mathematics.
- Accelerating reduction and scan using tensor core units. In Proceedings of the ACM International Conference on Supercomputing, ICS ’19, pages 46–57, New York, NY, USA, June 2019. Association for Computing Machinery.
- Numerical Behavior of the NVIDIA Tensor Cores, April 2020. Issue: 2020.10 Number: 2020.10.
- EGEMM-TC: accelerating scientific computing on tensor cores with extended precision. In Proceedings of the 26th ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, PPoPP ’21, pages 278–291, New York, NY, USA, February 2021. Association for Computing Machinery.
- Quantum-based Molecular Dynamics Simulations using Tensor Cores. arXiv:2107.02737 [physics, physics:quant-ph], July 2021. arXiv: 2107.02737 version: 1.
- On the Feasibility of Using Reduced-Precision Tensor Core Operations for Graph Analytics. In 2020 IEEE High Performance Extreme Computing Conference (HPEC), pages 1–7, September 2020. ISSN: 2643-1971.
- Verifying Random Quantum Circuits with Arbitrary Geometry Using Tensor Network States Algorithm. Physical Review Letters, 126(7):070502, February 2021. Publisher: American Physical Society.
- Harnessing GPU Tensor Cores for Fast FP16 Arithmetic to Speed up Mixed-Precision Iterative Refinement Solvers. In SC18: International Conference for High Performance Computing, Networking, Storage and Analysis, pages 603–613, November 2018.
- IBM. IBM Power Systems Announces POWER10 Processor. https://www.ibm.com/blogs/systems/ibm-power-systems-announces-power10-processor/, 2020.
- Intel. Ponte Vecchio. https://download.intel.com/newsroom/2021/client-computing/intel-architecture-day-2021-presentation.pdf, 2021.
- Dissecting the NVIDIA Volta GPU Architecture via Microbenchmarking. arXiv:1804.06826 [cs], April 2018. arXiv: 1804.06826.
- In-Datacenter Performance Analysis of a Tensor Processing Unit. In Proceedings of the 44th Annual International Symposium on Computer Architecture, ISCA ’17, pages 1–12, New York, NY, USA, June 2017. Association for Computing Machinery.
- Closing the ”quantum supremacy” gap: achieving real-time simulation of a random quantum circuit using a new Sunway supercomputer. In Proceedings of the International Conference for High Performance Computing, Networking, Storage and Analysis, SC ’21, pages 1–12, New York, NY, USA, November 2021. Association for Computing Machinery.
- NVIDIA Tensor Core Programmability, Performance & Precision. arXiv:1803.04014 [cs], March 2018.
- DGEMM Using Tensor Cores, and Its Accurate and Reproducible Versions. In High Performance Computing, Lecture Notes in Computer Science, pages 230–248, Cham, 2020. Springer International Publishing.
- NVIDIA. NVIDIA A100 TENSOR CORE GPU. https://images.nvidia.com/aem-dam/en-zz/Solutions/data-center/nvidia-ampere-architecture-whitepaper.pdf, 2020.
- NVIDIA. NVIDIA AMPERE GA102 GPU Architecture V1. https://images.nvidia.com/aem-dam/en-zz/Solutions/geforce/ampere/pdf/NVIDIA-ampere-GA102-GPU-Architecture-Whitepaper-V1.pdf, 2020.
- NVIDIA. NVIDIA AMPERE GA102 GPU Architecture V2. https://www.nvidia.com/content/PDF/nvidia-ampere-ga-102-gpu-architecture-whitepaper-v2.pdf, 2020.
- Randomized SVD on Tensor Cores. ISC High Performance, Research poster, June 2020.
- Error-free transformations of matrix multiplication by using fast routines of matrix multiplication and its applications. Numerical Algorithms, 59(1):95–118, January 2012.
- Preferred Networks. MN-Core - Accelerator for Deep Learning. https://projects.preferred.jp/mn-core/en/, 2018.
- Modeling Deep Learning Accelerator Enabled GPUs. arXiv:1811.08309 [cs], February 2019. arXiv: 1811.08309.
- The Effectiveness of Low-Precision Floating Arithmetic on Numerical Codes: A Case Study on Power Consumption. pages 199–206, January 2020.
- Optimizing the Fast Fourier Transform Using Mixed Precision on Tensor Core Hardware. In 2018 IEEE 25th International Conference on High Performance Computing Workshops (HiPCW), pages 3–7, December 2018.
- Establishing the quantum supremacy frontier with a 281 Pflop/s simulation. Quantum Science and Technology, 5(3):034003, April 2020. Publisher: IOP Publishing.
- Roofline: an insightful visual performance model for multicore architectures. Communications of the ACM, 52(4):65–76, April 2009.
- Accelerating sparse matrix–matrix multiplication with GPU Tensor Cores. Computers & Electrical Engineering, 88:106848, December 2020.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Collections
Sign up for free to add this paper to one or more collections.

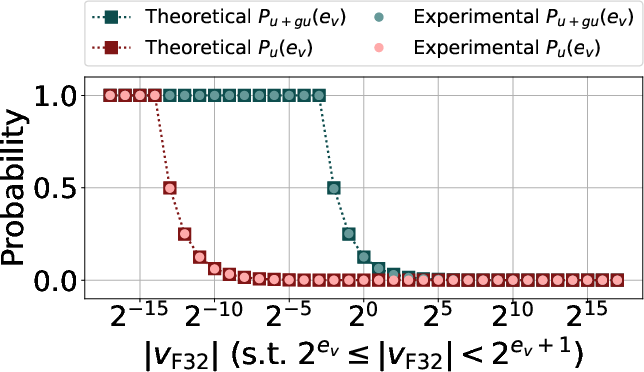 *Figure 2: The theoretical and experimental probability of underflow
*Figure 2: The theoretical and experimental probability of underflow 


