Next Generation Reservoir Computing (2106.07688v2)

Abstract: Reservoir computing is a best-in-class machine learning algorithm for processing information generated by dynamical systems using observed time-series data. Importantly, it requires very small training data sets, uses linear optimization, and thus requires minimal computing resources. However, the algorithm uses randomly sampled matrices to define the underlying recurrent neural network and has a multitude of metaparameters that must be optimized. Recent results demonstrate the equivalence of reservoir computing to nonlinear vector autoregression, which requires no random matrices, fewer metaparameters, and provides interpretable results. Here, we demonstrate that nonlinear vector autoregression excels at reservoir computing benchmark tasks and requires even shorter training data sets and training time, heralding the next generation of reservoir computing.

• The paper introduces NG-RC, a nonlinear vector autoregression method that replaces complex random reservoirs with engineered time-delayed feature vectors for modeling dynamical systems.
• It achieves efficient forecasting with up to 33-162x faster training speeds and state-of-the-art performance on chaotic systems using as few as 400 training points.
• The method trains only the output weights via regularized linear regression, significantly reducing metaparameter tuning and eliminating randomness issues in traditional reservoir computing.

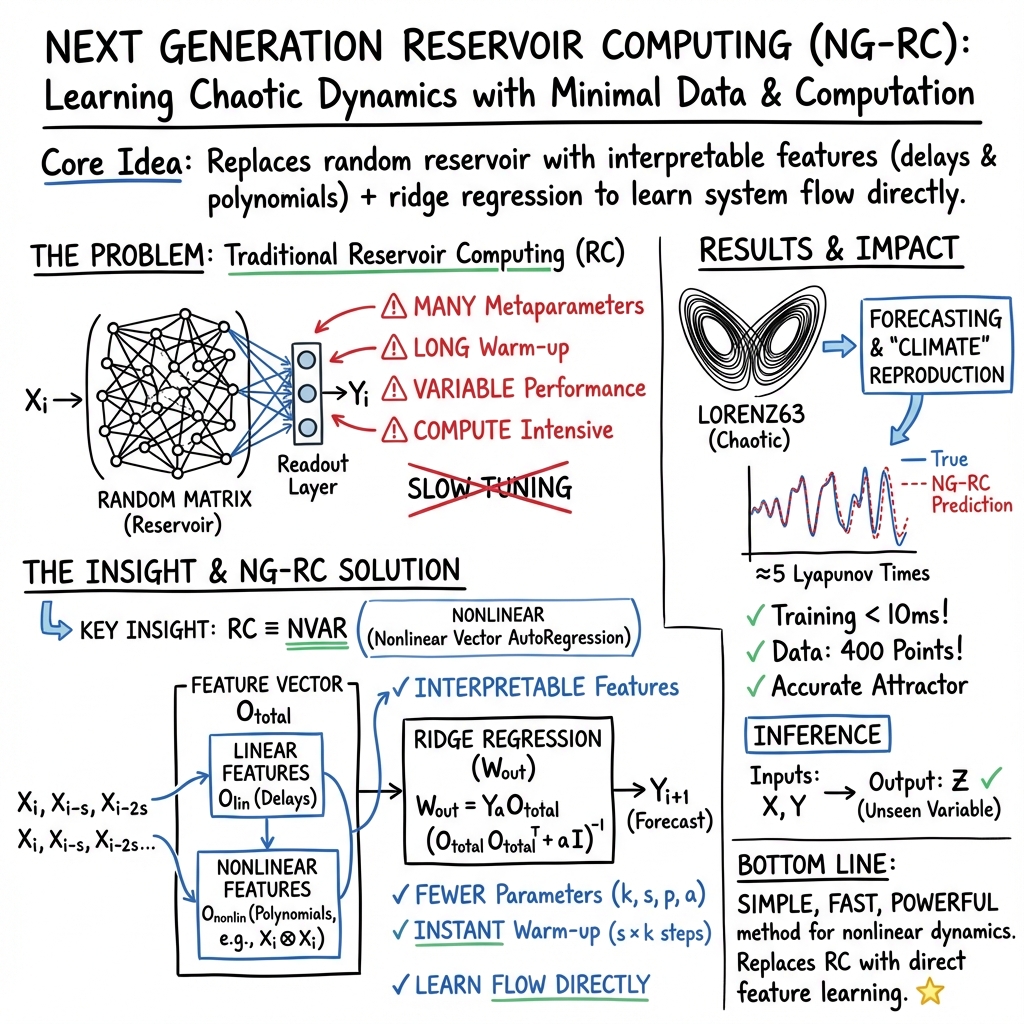
This paper, "Next Generation Reservoir Computing" (Next Generation Reservoir Computing, 2021), introduces Nonlinear Vector Autoregression (NVAR), termed the Next Generation Reservoir Computer (NG-RC), as a practical and more efficient alternative to traditional Reservoir Computing (RC) for modeling and forecasting dynamical systems from time-series data.

Traditional RC, while effective for dynamical systems tasks and less data-hungry than some deep learning methods, relies on randomly initialized and fixed reservoir connections and input weights. This introduces variability in performance depending on the random matrices used and necessitates extensive tuning of numerous metaparameters. The NG-RC addresses these issues by demonstrating that the functional capability of a traditional RC with a linear reservoir and nonlinear output layer is mathematically equivalent to an NVAR model.

The core idea of the NG-RC is to replace the complex, random recurrent neural network (the reservoir) with a simple feature vector constructed directly from time-delayed observations of the input data and nonlinear functions of these observations. This feature vector, $O_{total,i}$, for a given time step $i$, is typically composed of:

1. A constant term ($c$).
2. Linear features ($O_{lin,i}$): Concatenation of the input vector $X$ at the current time $t_i$ and at $k-1$ previous time steps, spaced by $s$. If $X_i$ is $d$-dimensional, $$O_{lin,i} = X_i \oplus X_{i-s} \oplus X_{i-2s} \oplus \ldots \oplus X_{i-(k-1)s}$$. This results in a feature vector of size $d \times k$.
3. Nonlinear features ($O_{nonlin,i}$): Nonlinear functions of the linear features, typically monomials (polynomials). For a quadratic feature vector $O^{(2)}_{nonlinear}$, it includes all unique quadratic terms of the elements in $O_{lin,i}$. A p-order polynomial feature vector $O^{(p)}_{nonlinear}$ consists of all unique monomials of order up to $p$ of the elements in $O_{lin,i}$.

The total feature vector is $O_{total} = c \oplus O_{lin} \oplus O_{nonlin}$.

The output $Y_{i+1}$ is then computed as a linear transformation of this feature vector:

$Y_{i+1} = W_{out} O_{total,i+1}$

Instead of directly predicting $Y_{i+1}$, the paper shows improved performance by training the NG-RC to predict the difference between consecutive time steps, effectively learning the "flow" of the dynamical system:

$Y_{i+1} = Y_i + W_{out} O_{total,i+1}$

The output weights $W_{out}$ are the only parameters that need training. This is done using supervised learning via regularized linear least squares (specifically, Tikhonov regularization or ridge regression). Given a training dataset of input-output pairs $(O_{total}, Y_{target})$, the optimal $W_{out}$ is found by minimizing a cost function that includes both the mean squared error and a regularization term penalizing large weights:

$$W_{out} = Y_{target} O_{total}^T (O_{total} O_{total}^T + \alpha I)^{-1}$$

Here, $\alpha$ is the regularization parameter controlling the strength of the penalty, and $I$ is the identity matrix. This linear optimization is computationally efficient and avoids complex backpropagation or reservoir state optimization.

Practical Implementation Aspects and Advantages:

• Reduced Data Requirement: NG-RC requires significantly less training data compared to traditional RC or deep learning methods. The authors demonstrate state-of-the-art performance on benchmark chaotic systems (Lorenz63 and a double-scroll circuit) using only 400 training data points, a drastically smaller amount than typical requirements for traditional RCs (thousands to millions of points). The minimum data needed is hypothesized to be related to the number of unknown fit parameters ($N_{total} \times d$), plus some overhead for generalization.
• Faster Training: Training involves constructing the feature matrix from the time series and performing a single linear regression. This is computationally much cheaper than training the weights of a recurrent neural network. The paper estimates speed-ups of 33-162x compared to an efficient traditional RC and over 10⁶x for a high-accuracy traditional RC for the Lorenz63 task.
• Fewer Metaparameters: The primary metaparameters to tune are $k$ (number of delays), $s$ (delay spacing), the polynomial order $p$, and the regularization parameter $\alpha$. This is a much smaller and more interpretable set than the large number of parameters in traditional RC reservoirs (spectral radius, connectivity sparsity, input scaling, etc.). The authors find small values of $k$ and low polynomial orders ($p=2, 3$) are often sufficient.
• Shorter Warm-up Period: Traditional RCs require a "warm-up" phase to allow the reservoir state to become independent of initial conditions. NG-RC only needs $s \times k$ steps to populate the initial feature vector, which is typically very short (e.g., 2 steps for $k=2, s=1$).
• Avoids Randomness Issues: Since there is no randomly generated reservoir matrix, the performance is deterministic given the hyperparameters, removing the need to generate and test multiple random instances.
• Interpretability: Although not deeply explored in the paper, the trained output weights $W_{out}$ directly map combinations of past states ($O_{total}$) to future changes. Analyzing $W_{out}$ can potentially provide insights into which past states and nonlinear interactions are most predictive of the system's dynamics.

Application Examples Demonstrated in the Paper:

1. Forecasting Chaotic Dynamics: NG-RC successfully forecasts the dynamics of Lorenz63 and the double-scroll circuit for several Lyapunov times and reconstructs their strange attractors, matching the long-term statistical properties ('climate'). This is achieved with minimal training data and computational cost.
2. Inferring Unseen Dynamics: NG-RC can infer missing variables of a dynamical system. For Lorenz63, it was trained on all three variables ($x, y, z$) but tested by inferring $z$ given only $x$ and $y$. This is relevant for applications where only partial state information is available.

Implementation Details & Code:

The paper notes that the implementation uses standard Python libraries like NumPy and SciPy. The core steps for implementation would be:

1. Data Collection: Obtain time-series data $X(t)$ from the dynamical system. Discretize it with a suitable time step $dt$.
2. Feature Engineering: For each time step $i$ in the training data, construct the feature vector $O_{total,i}$ by collecting delayed inputs ($X_i, X_{i-s}, \ldots, X_{i-(k-1)s}$) and their chosen nonlinear combinations (e.g., quadratic or cubic monomials). Include a constant term if desired.
3. Target Variable Preparation: Determine the target output $Y_{target,i}$. For forecasting the flow, this would be $Y_{target,i} = X_{i+1} - X_i$. For direct prediction, it would be $Y_{target,i} = X_{i+1}$.
4. Training: Stack the feature vectors $O_{total,i}$ row-wise into a matrix $\mathbf{O}_{total}$ and the target variables $Y_{target,i}$ row-wise into a matrix $\mathbf{Y}_{target}$. Compute the output weight matrix $W_{out}$ using the Tikhonov regularization formula:

   # Using NumPy for linear algebra # O_total is the matrix where each row is a feature vector # Y_target is the matrix where each row is the target output # alpha is the regularization parameter identity_matrix = np.eye(O_total.shape[1]) # W_out = Y_target @ O_total.T @ np.linalg.inv(O_total @ O_total.T + alpha * identity_matrix) # Potentially unstable # More stable using least squares solver W_out = np.linalg.solve(O_total.T @ O_total + alpha * identity_matrix, O_total.T @ Y_target).T

5. Prediction/Forecasting:
   • Start with the last known state $X_{last}$.
   • Construct the feature vector $O_{total, last}$ using $X_{last}$ and required past states $X_{last-s}, \ldots$.
   • Predict the change (or next state): $\Delta X = W_{out} O_{total, last}$ (or $X_{next} = W_{out} O_{total, last}$).
   • Update the state: $X_{next} = X_{last} + \Delta X$ (or $X_{next} = X_{next}$).
   • Repeat, using the predicted $X_{next}$ as the input for the next step's feature vector calculation.

The authors provide their code publicly on GitHub (link provided in the paper), which can serve as a direct reference for implementation.

Computational Considerations:

The dominant computational cost during training is solving the linear system for $W_{out}$, which is $O(M_{train} N_{total}^2 + N_{total}^3)$ where $M_{train}$ is the number of training points and $N_{total}$ is the number of features. During forecasting, the cost per time step is simply multiplying the feature vector by $W_{out}$, which is $O(N_{total} \times d_{out})$ where $d_{out}$ is the dimension of the output. Since $M_{train}$ and $N_{total}$ are typically small in NG-RC compared to traditional methods, the overall cost is low. The number of features $N_{total}$ grows polynomially with $d$ and $k$, and with the polynomial order $p$. Choosing small values for these parameters is key to computational efficiency.

Robustness and Limitations:

The paper demonstrates robustness to noise by showing that increasing the regularization parameter $\alpha$ allows the NG-RC to learn the underlying deterministic system even in the presence of significant noise. While the paper focuses on low-dimensional systems, the theoretical equivalence suggests applicability to high-dimensional systems where traditional RC has been successful. Future work includes exploring better feature selection methods (like LASSO) or kernel methods, especially when $N_{total}$ becomes large.

In summary, the NG-RC offers a computationally efficient, data-thrifty, and conceptually simpler method for modeling and forecasting dynamical systems by leveraging the power of nonlinear regression on time-delayed input features, providing a strong practical alternative to traditional reservoir computing approaches.