General solution of the exceptional Hermite differential equation and its minimal surface representation (2004.09250v2)

Abstract: The main aim of this paper is the study of the general solution of the exceptional Hermite differential equation with fixed partition $\lambda = (1)$ and the construction of minimal surfaces associated with this solution. We derive a linear second-order ordinary differential equation associated with a specific family of exceptional polynomials of codimension two. We show that these polynomials can be expressed in terms of classical Hermite polynomials. Based on this fact, we demonstrate that there exists a link between the norm of an exceptional Hermite polynomial and the gap sequence arising from the partition used to construct this polynomial. We find the general analytic solution of the exceptional Hermite differential equation which has no gap in its spectrum. We show that the spectrum is complemented by non-polynomial solutions. We present an implementation of the obtained results for the surfaces expressed in terms of the general solution making use of the classical Enneper-Weierstrass formula for the immersion in the Euclidean space $\mathbb{E}^3$, leading to minimal surfaces. Three-dimensional displays of these surfaces are presented.

• The paper presents a comprehensive derivation of the exceptional Hermite differential equation’s solution, bridging gaps in the classical spectrum.
• It employs the Enneper-Weierstrass immersion formula to construct minimal surfaces that reveal symmetry and singularity properties.
• Implementation insights include symbolic computation with recursive formulas and hypergeometric functions to analyze both polynomial and non-polynomial solutions.

General Solution of the Exceptional Hermite Differential Equation

Introduction

The paper explores the general solution of the exceptional Hermite differential equation with a fixed partition $\lambda = (1)$. The paper establishes connections between exceptional Hermite polynomials and classical Hermite polynomials, deriving a more comprehensive analytical solution for the Hermite differential equation without gaps in its spectrum. The research further constructs minimal surfaces associated with these solutions using the Enneper-Weierstrass immersion formula.

Exceptional Hermite Polynomials

Exceptional orthogonal polynomials (XOPs) offer extensions to classical polynomial families, removing traditional orthogonality constraints at finite points. The research focuses on the exceptional Hermite polynomials defined by a fixed partition $\lambda = (1)$, establishing a connection to classical Hermite polynomials. The polynomials in question coincide with traditional Hermite polynomials, except with a gap sequence in their spectrum due to the partition's structure.

Figure 1: Minimal surface representation of the general solution omega_n(z), for n=1.

General Solution and Minimal Surfaces

The paper derives the general solution of the associated exceptional Hermite differential equation using series expansion techniques and highlights how non-polynomial solutions supplement the spectrum. This expanded spectrum includes polynomial solutions generally expressed in series form. For instance, the solution involves extensions of classical Hermite polynomials to negative indices, leading to non-polynomial solutions for $n=1, 2$.

The Enneper-Weierstrass immersion formula is employed to generate minimal surface representations for the general solution. The surfaces visualize the analytical solution's properties, revealing symmetry and singularity points that illuminate the structure and behavior of these polynomials in Euclidean space.

Implementation Insights

Implementing this model involves leveraging computational tools like Mathematica for symbolic calculations and graphical representations. The essential steps include computing Hermite solutions through recursive formulas and utilizing hypergeometric functions to approximate complex integrals involved in minimal surface evaluations.

Key implementation challenges may arise in handling non-polynomial solutions derived from extended indices and large computational loads when visualizing intricate surface geometries.

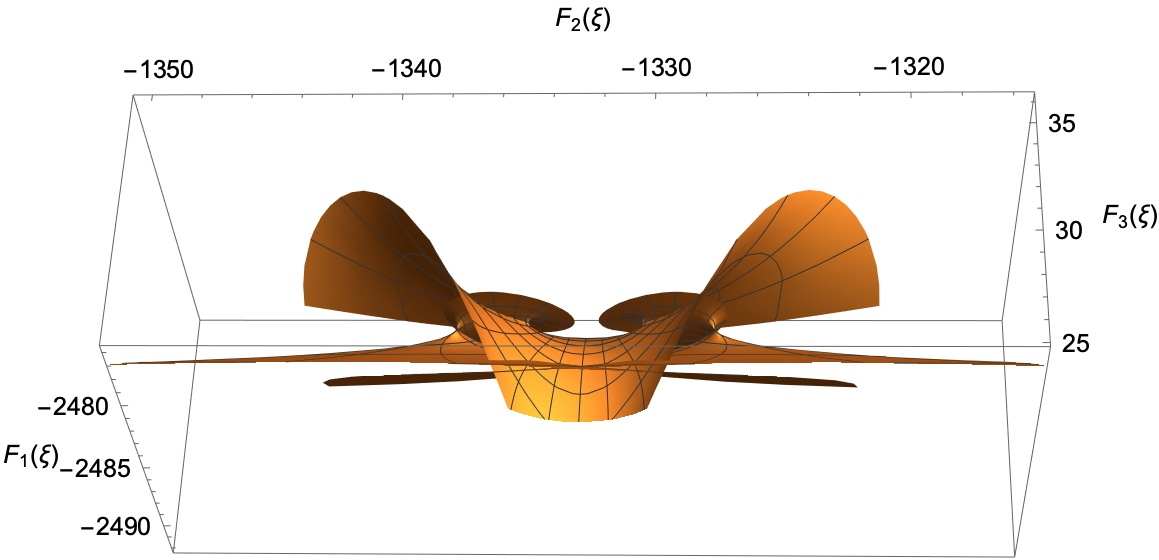
Figure 2: Minimal surface representation of the general solution omega_n(z), for n=2.

Conclusion

This exposition of the exceptional Hermite differential equation bridges mathematical theory with geometric interpretation, offering new insights into polynomial-based systems and their broader applications. The research provides foundational tools and methodologies for future exploration across mathematical physics and potentially other fields relying on special functions and orthogonal polynomials.

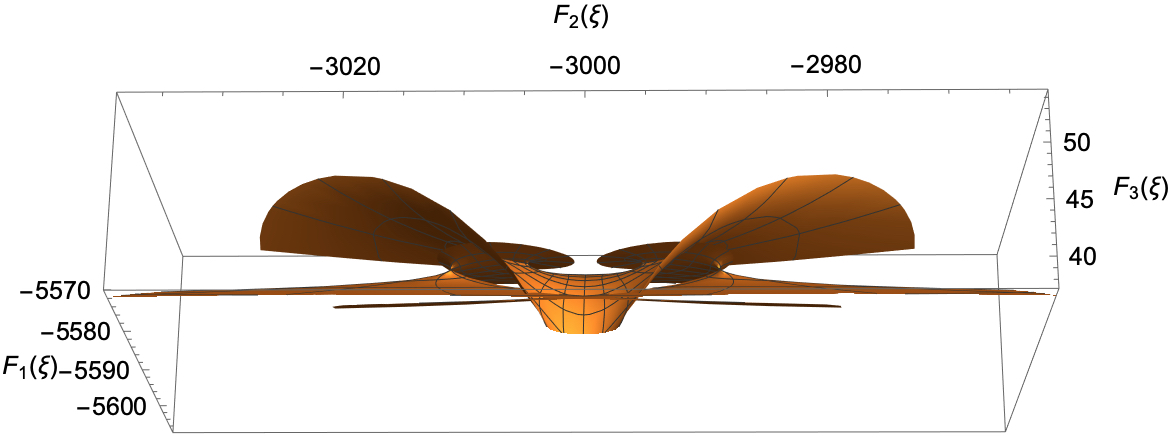
Figure 3: Minimal surface representation of the general solution omega_n(z), for n=3.