- The paper introduces a dual-engine pipeline comprising the Observer Engine for object detection and the Physicist Engine for symbolic regression.
- It leverages Faster-RCNN and genetic programming to accurately extract physical properties and derive underlying mathematical equations.
- Experiments demonstrate successful inference of dynamic equations with precise physical constants across diverse scenarios.
Perceiving Physical Equation by Observing Visual Scenarios
Introduction
The paper "Perceiving Physical Equation by Observing Visual Scenarios" (1811.12238) introduces a novel approach to inferring physical equations from visual scenarios, a task that involves deriving mathematical expressions for object dynamics directly from video data. The paper presents a pipeline composed of two main components: the Observer Engine and the Physicist Engine. The Observer Engine uses neural networks to extract physical properties from video frames, while the Physicist Engine applies symbolic regression to infer the underlying mathematical equations representing object dynamics.
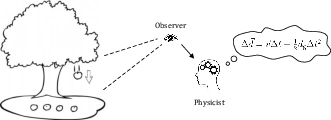
Figure 1: Observing and thinking: inferring physical equation from visual scenario. The ability to infer universal law of the environment is one of the significant high-level aspects of human intelligence.
Model Architecture
Observer Engine
The Observer Engine is responsible for observing video scenarios and extracting relevant physical properties of moving objects. The authors employ a Faster-RCNN model to detect and localize objects precisely, using a two-stage approach to improve the accuracy of position estimation. The physical properties such as position and velocity are extracted and provided as input to the Physicist Engine.
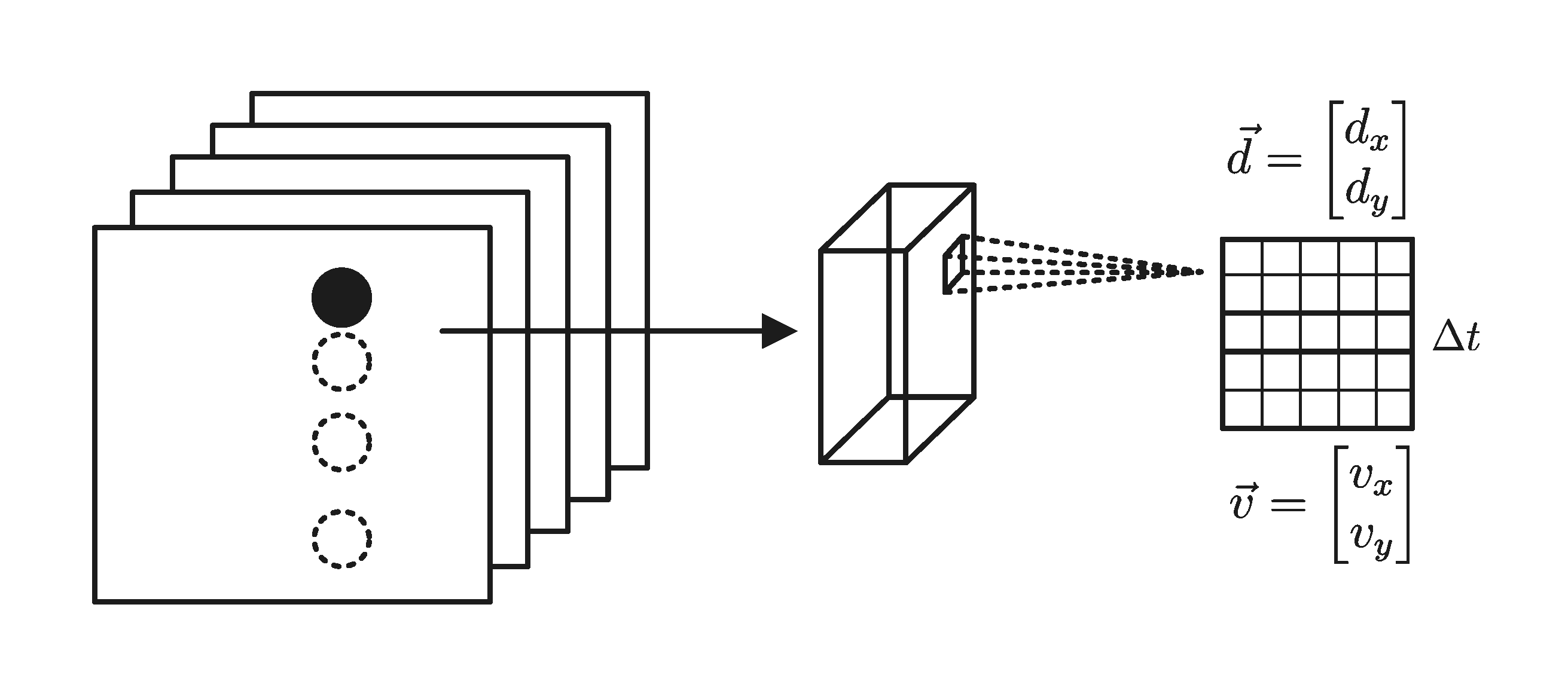
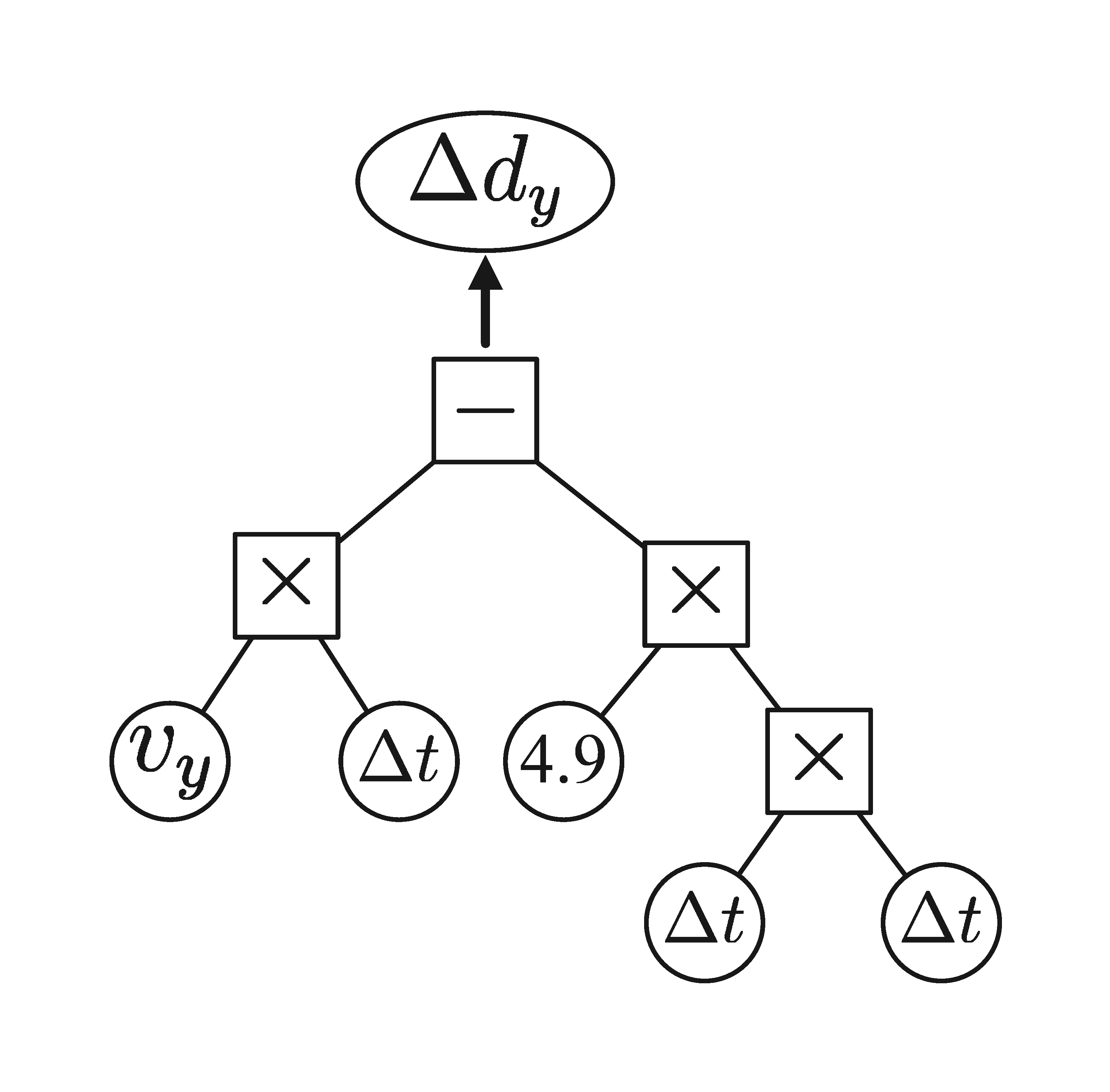
Figure 2: Our model is comprised of (a) the Observer Engine and (b) the Physicist Engine. At left, a video depicts that an object is in free-falling. The Observer Engine uses deep neural networks to extract the physical properties of the object. The Physicist Engine learns a mathematical expression of the object dynamics by evolving a syntax tree based on the property variables.
Physicist Engine
The Physicist Engine, inspired by symbolic regression, derives mathematical equations that describe object dynamics. It uses genetic programming to evolve syntax trees representing equations aiming at minimizing the error between predicted and observed dynamics. The approach allowed for the discovery of equations with accurate physical constants across different scenarios.
Experiments and Results
The experiments conducted on synthetic video data demonstrate the effectiveness of the pipeline in perceiving physical equations in diverse scenarios such as drift, free-falling, parabola motion, slope movement, and spring dynamics. The Observer Engine achieved high precision in object localization, while the Physicist Engine was able to correctly infer equations, as evidenced by accurate physical constants estimation.









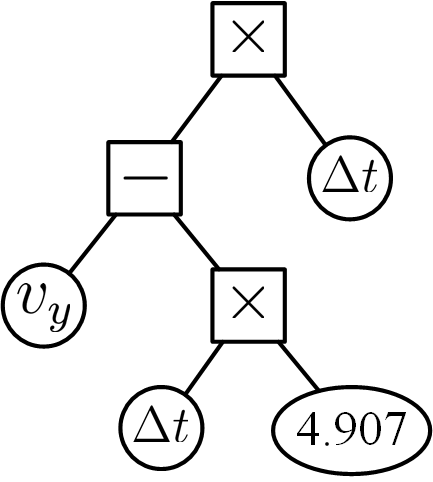



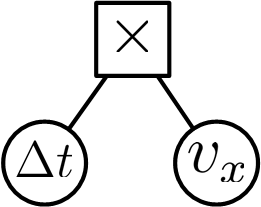
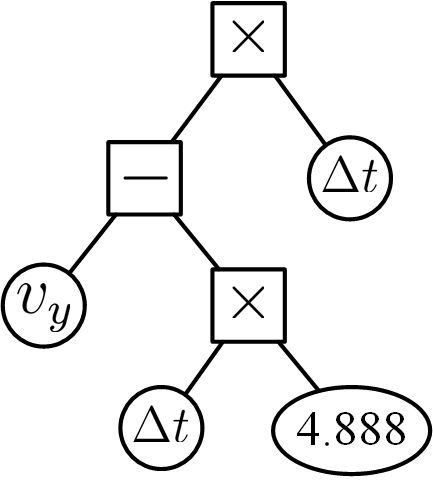



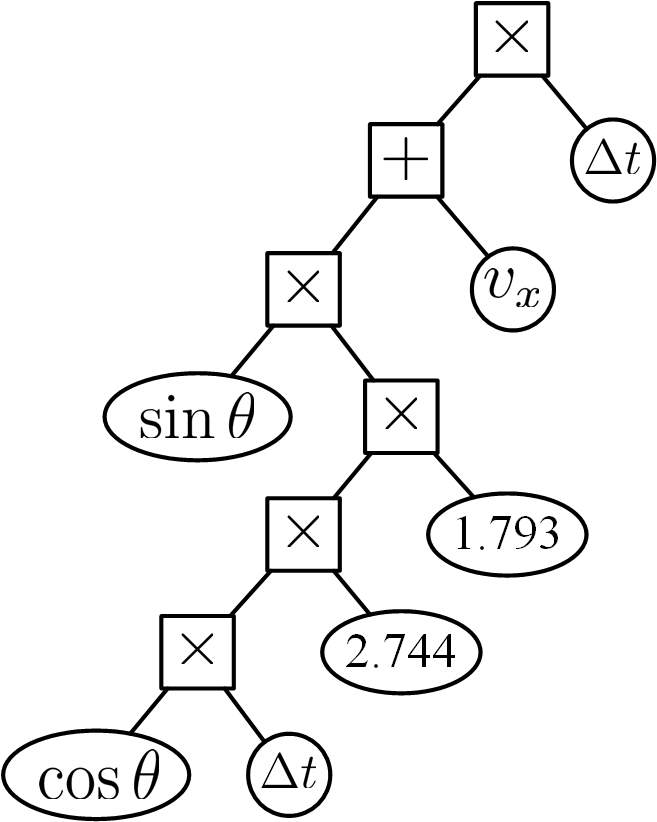
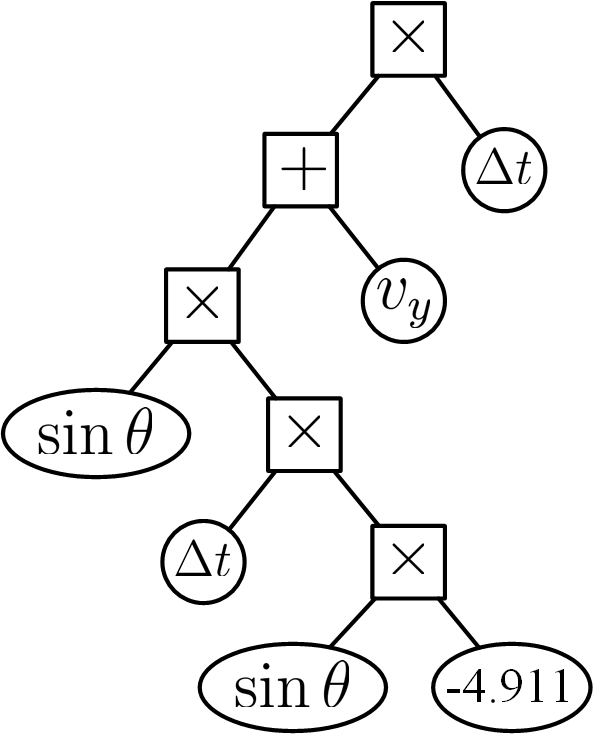




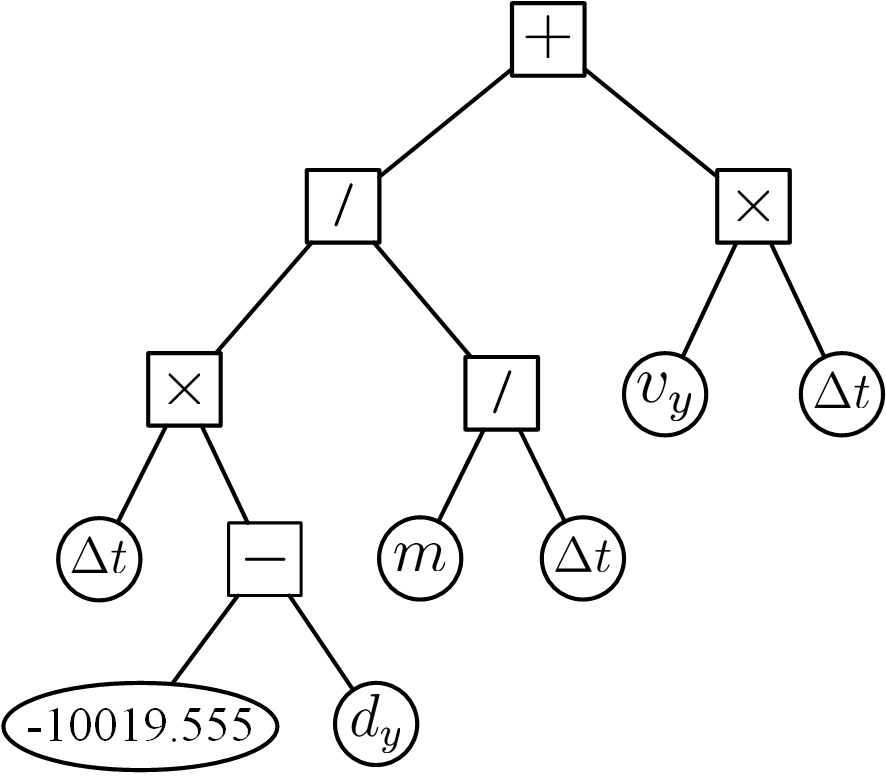
Figure 3: Physical scenarios and our learned equations. In each scenario, the object moves under particular dynamic equations. Results show that our method is able to learn correct mathematical equations with relatively accurate physical constants in all of the scenarios. The syntax trees are shown together with the equations.
Implementation Details
The implementation of the Observer Engine leverages a two-stage architecture of Faster-RCNN detectors to achieve sub-pixel localization accuracy, whereas the Physicist Engine uses genetic programming to evolve candidate equations robustly over multiple generations. The engines are configured with specific hyperparameters for learning rate and batch size, ensuring convergence and high detection accuracy. Symbolic regression was particularly effective, surpassing traditional regression methods in accurately representing complex physical laws.
Implications and Future Work
This research offers an innovative framework for understanding and reasoning about physical dynamics directly from visual data. The implications extend to potential applications in experimental physics and automated scientific discovery, where complex systems can be analyzed without manual equation derivation. For future work, the integration of the pipeline into real-world scenarios, extension to multi-object systems, and exploration of hybrid models combining deep learning with symbolic reasoning stand as promising directions.
Conclusion
The paper provides significant advancements in AI research by proposing a method capable of perceiving physical equations from visual environments. It successfully blends computer vision and symbolic regression techniques to represent physical dynamics comprehensively and predictably. The work lays a foundation for subsequent studies aiming to develop automated systems for scientific reasoning and discovery in AI.

Figure 4: Baselines of the Physicist Engine.



























