Hilbert geometry of the symmetric positive-definite bicone: Application to the geometry of the extended Gaussian family (2508.14369v1)

Abstract: The extended Gaussian family is the closure of the Gaussian family obtained by completing the Gaussian family with the counterpart elements induced by degenerate covariance or degenerate precision matrices, or a mix of both degeneracies. The parameter space of the extended Gaussian family forms a symmetric positive semi-definite matrix bicone, i.e. two partial symmetric positive semi-definite matrix cones joined at their bases. In this paper, we study the Hilbert geometry of such an open bounded convex symmetric positive-definite bicone. We report the closed-form formula for the corresponding Hilbert metric distance and study exhaustively its invariance properties. We also touch upon potential applications of this geometry for dealing with extended Gaussian distributions.

• The paper introduces a closed-form Hilbert metric for the extended Gaussian family’s SPD bicone, enabling efficient computation using only extreme eigenvalues.
• It rigorously characterizes the isometries of the variance-precision manifold through identity-complement and orthonormal conjugation invariances.
• The study highlights computational advantages for applications like DTI and clustering by leveraging the derived geometric framework.

Hilbert Geometry of the Symmetric Positive-Definite Bicone and Its Application to the Extended Gaussian Family

Introduction and Motivation

The paper investigates the Hilbert geometry of the symmetric positive-definite bicone, which arises as the parameter space of the extended Gaussian family. The extended Gaussian family is defined as the closure of the standard Gaussian family, incorporating elements with degenerate covariance and/or precision matrices. This extension leads to a parameter space that is a bicone: two partial symmetric positive semi-definite (PSD) cones joined at their bases, rather than the apex. The paper is motivated by the need to understand the geometric and metric properties of this space, particularly for applications involving degenerate Gaussian distributions and open stochastic systems.

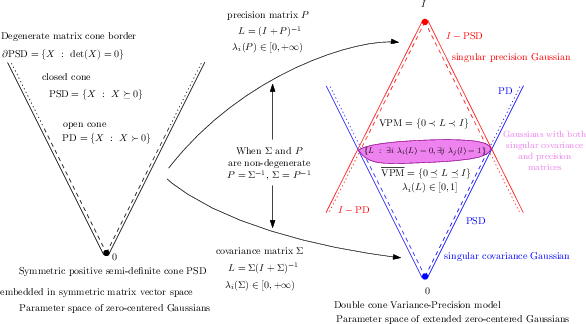
Figure 1: The parameter space of the extended Gaussian family forms a closed double cone.

The Extended Gaussian Family and the Variance-Precision Model

The standard $n$-variate zero-centered Gaussian distribution is parameterized by a symmetric positive-definite covariance matrix $\Sigma \in PD(n)$ or equivalently by its precision matrix $P = \Sigma^{-1}$. The extended Gaussian family includes distributions with degenerate covariance or precision matrices, leading to a parameter space that is the intersection of two PSD cones. This intersection, termed the variance-precision manifold (VPM), is defined as:

$VPM(n) = \{ X \in Sym(n) : 0 \prec X \prec I \}$

where $\prec$ denotes the Loewner order.

In two dimensions, the PSD cone $PSD(2)$ can be visualized as a Lorentz cone in $\mathbb{R}^3$, and the VPM as the intersection of two such cones, forming a double Lorentz cone.

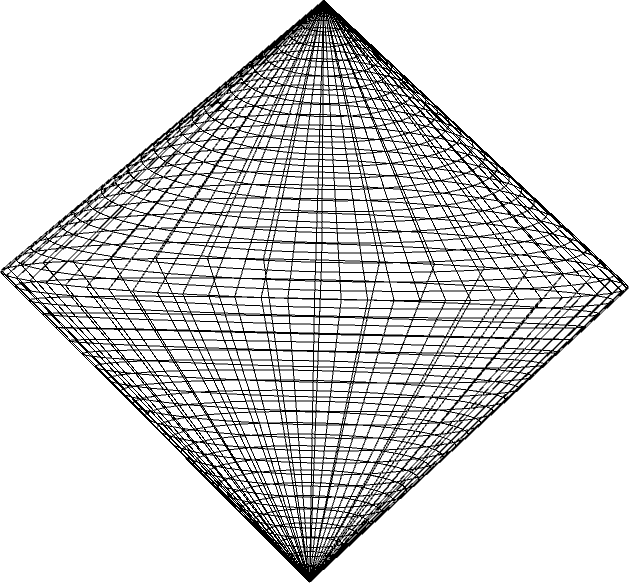
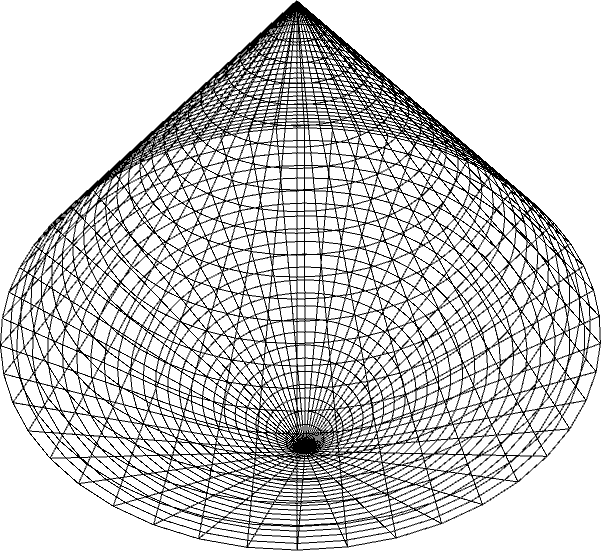
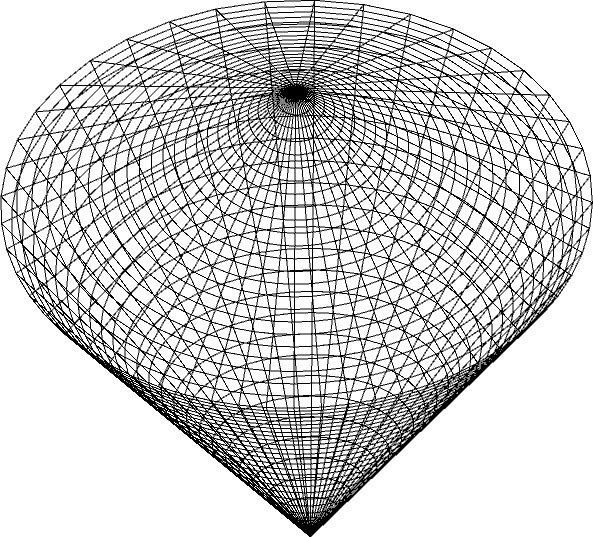
Figure 2: The parameter space of (2) can be viewed as a double Lorentz cone in $\mathbb{R}^3$: Three views of the double Lorentz cone.

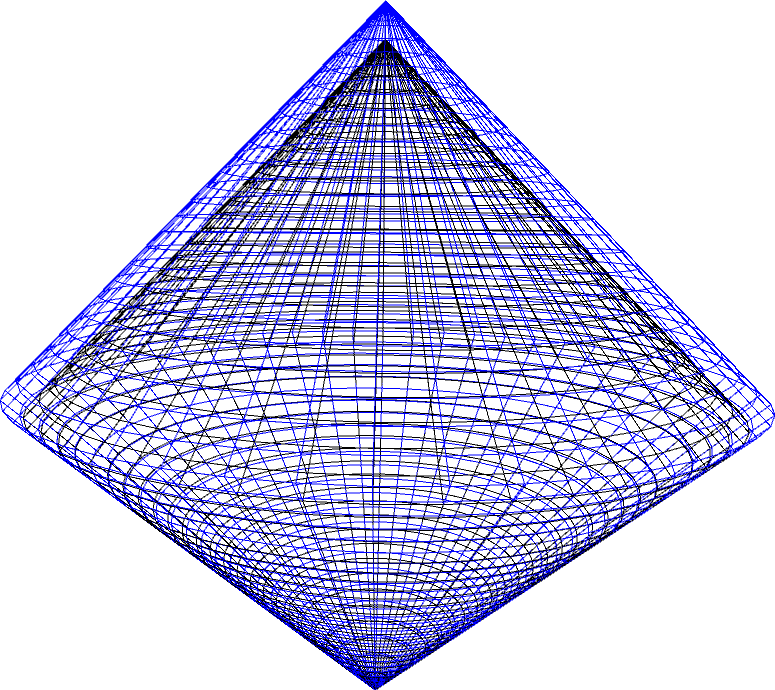
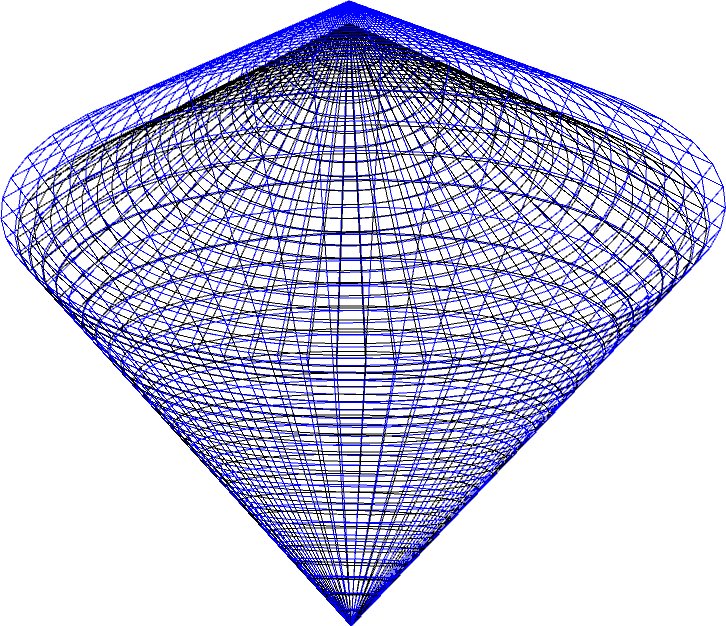
Figure 3: The parameter space of $(2)$ (viewed as a Lorentz bicone in $\mathbb{R}^3$): Three views of the boundary of the Lorentz bicone with $VPM$ (in blue) encapsulating $PD$ (in black).

Hilbert and Birkhoff Geometries: Definitions and Relationships

Hilbert geometry is defined on any open bounded convex domain $C$ in a Hilbert space, with the Hilbert metric $d_H$ ensuring that straight lines are geodesics. Birkhoff projective geometry, defined on open regular cones, introduces a projective distance $d_B$ that is invariant under positive scaling. The Hilbert metric on a convex domain $C$ can be characterized via the Birkhoff metric on the projective space of the cone over $C$.

For the VPM, the Hilbert metric is given in closed form:

$$d_H(A, B) = \log \frac{\max(\lambda_{\max}, \mu_{\max})}{\min(\lambda_{\min}, \mu_{\min})}$$

where $\lambda_{\min}, \lambda_{\max}$ are the minimal and maximal eigenvalues of $B^{-1}A$, and $\mu_{\min}, \mu_{\max}$ are those of $(I-B)^{-1}(I-A)$.

Invariance Properties and Isometry Characterization

The Hilbert metric on VPM exhibits two key invariance properties:

• Identity-complement invariance: The map $X \mapsto I - X$ is an isometry.
• Orthonormal conjugation invariance: The map $X \mapsto U^\top X U$ for $U \in O(n)$ is an isometry.

These invariances are analogous to the invariance under inversion and congruence for the affine-invariant Riemannian metric (AIRM) on $PD(n)$, but the Hilbert VPM metric is only invariant under orthonormal (not general invertible) congruence.

The paper rigorously proves that these two transformations generate the full isometry group of the VPM for $n > 1$, using projective geometry and cone automorphism theory. The isometries of the Hilbert metric on VPM are precisely the collineations induced by these transformations.

Computational and Geometric Implications

The closed-form Hilbert metric on VPM requires only the four extreme eigenvalues of two matrices, in contrast to the AIRM, which requires the full spectrum. This computational advantage is significant for applications such as Diffusion Tensor Imaging (DTI), where efficient metric computation is critical.

The paper also discusses the monotonicity property of Hilbert distances for nested VPM domains, showing that enlarging the domain allows for bounded distances even for degenerate matrices. This is relevant for algorithms that must handle mixtures of degenerate covariance and precision matrices.

Figure 4: Fine approximation of the smallest enclosing ball (SEB, in red) with respect to the Hilbert VPM distance in 2D of a set of 2D SPD matrices (or equivalently, 2D zero-centered Gaussians, in black).

The geometric structure of VPM, with straight lines as geodesics, facilitates the implementation of computational geometry primitives such as smallest enclosing balls and Voronoi diagrams, which are useful in clustering and other machine learning tasks.

Extensions and Future Directions

The framework can be extended to full Gaussian families (with nonzero means) via the Calvo-Oller embedding, mapping $(\mu, \Sigma)$ to a higher-dimensional SPD cone and then to VPM. The paper also suggests investigating the subdomain of correlation matrices (elliptope) within VPM, which has applications in statistics and machine learning.

Further work is proposed on the facial characterization of VPM and its extensions, as well as the development of algorithms leveraging the Hilbert geometry for degenerate Gaussian models.

Conclusion

This paper provides a comprehensive geometric and metric analysis of the symmetric positive-definite bicone, the parameter space of the extended Gaussian family. By deriving a closed-form Hilbert metric and fully characterizing its isometries, the work lays a foundation for efficient computation and robust handling of degenerate Gaussian distributions. The results have direct implications for computational geometry, statistical modeling, and machine learning, particularly in scenarios involving degenerate covariance and precision structures. Future research will likely focus on algorithmic applications, further geometric extensions, and the integration of these concepts into practical systems for data analysis and inference.