Quasiprobability Thermodynamic Uncertainty Relation (2508.14354v1)

Abstract: We derive a quantum extension of the thermodynamic uncertainty relation where dynamical fluctuations are quantified by the Terletsky-Margenau-Hill quasiprobability, a quantum generalization of the classical joint probability. The obtained inequality plays a complementary role to existing quantum thermodynamic uncertainty relations, focusing on observables' change rather than exchange of charges through jumps and respecting initial coherence. Quasiprobabilities show anomalous behaviors that are forbidden in classical systems, such as negativity; we reveal that such behaviors are necessary to reduce dissipation beyond classical limitations and show that they are stronger requirements than that the state has quantum coherence. To illustrate these statements, we employ a model that can exhibit a dissipationless heat current, which would be prohibited in classical systems; we construct a state that has much coherence but does not lead to a dissipationless current due to the absence of anomalous behaviors in quasiprobabilities.

• The paper establishes a quantum TUR that links entropy production and observable fluctuation via Terletsky-Margenau-Hill quasiprobability.
• It employs quantum master equations for Markovian open systems and a short-time variance method to rigorously quantify dissipation bounds.
• The findings suggest practical pathways for designing energy-efficient quantum systems by minimizing dissipation beyond classical limits.

Quasiprobability Thermodynamic Uncertainty Relation

Introduction

The paper "Quasiprobability Thermodynamic Uncertainty Relation" establishes a quantum extension of the thermodynamic uncertainty relation (TUR) by leveraging the concept of quasiprobability, specifically the Terletsky-Margenau-Hill (TMH) quasiprobability. Unlike traditional methods that involve classical joint probabilities, the TMH quasiprobability accounts for quantum mechanical properties such as negativity, which are indicative of quantum phenomena like contextuality.

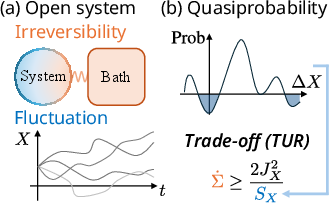
Figure 1: In open systems, dissipation and fluctuations are encapsulated in the thermodynamic uncertainty relation, where the product of entropy production rate $epr$ and dynamical fluctuation $S_X$ is bounded.

Main Contributions

The paper's primary contribution is the derivation of a quantum TUR that specifies a universal trade-off between dissipation, represented by the entropy production rate (EPR), and the dynamical fluctuation of an observable quantified through quasiprobability. This TUR is presented as:

$\epr(\rho) \geq \frac{2|J_X^\mathrm{d}(\rho)|^2}{m_X(\rho)},$

where $J_X^\mathrm{d}$ is the dissipative part of an observable's change, and $m_X$ is the short-time variance evaluated via the TMH quasiprobability. This establishes a rigorous lower bound on EPR, considering the quantum fluctuations of system observables.

Theoretical Framework

The paper is grounded in the framework of Markovian open quantum systems described by the quantum master equation. The paper critically analyzes the role of quasiprobabilities in defining the short-time moments of observable changes. By introducing the notion of short-time fluctuation $m_X^{(n)}$, the formulation allows for precise quantification of quantum mechanical effects on classical thermodynamic constraints.

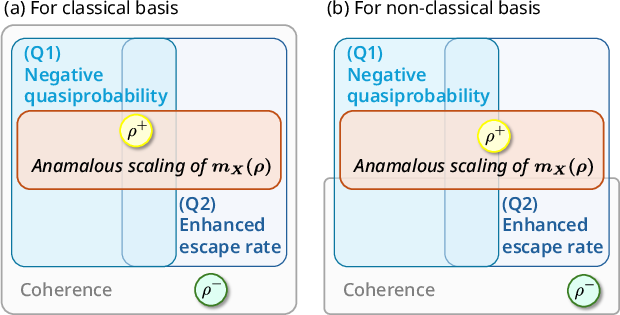
Figure 2: Hierarchy of conditions showing the necessary requirements for anomalous scaling in quantum systems, emphasizing the role of quasiprobability.

Comparison to Existing Methods

The approach is compared to existing quantum extensions of TURs, particularly those based on full counting statistics (FCS) and two-point measurements (TPM). The distinction lies in focusing on intrinsic observables that are not necessarily linked to environmental exchanges. Unlike TPM, the present method maintains coherence, offering a practical advantage by fully incorporating initial quantum states' coherence.

Anomalous Scaling

A significant discussion revolves around conditions for anomalous scaling, a phenomenon where the TUR's bound becomes significantly small. This behavior is attributed more fundamentally to non-classical characteristics of quasiprobabilities rather than just coherence. The paper identifies conditions under which quantum systems exhibit such scaling, providing new insights into minimizing dissipation beyond classical limits.

Practical Implications and Future Directions

The findings imply potential for more efficient energy systems that leverage quantum mechanical principles. In practical terms, systems designed using this TUR could achieve lower bounds of dissipation, pushing the boundaries of thermodynamic efficiency. Future exploration could integrate quasiprobability concepts with broader stochastic thermodynamic frameworks, potentially leading to breakthroughs in energy conversion and quantum computing efficiencies.

Conclusion

The derived quantum TUR based on quasiprobability provides a robust theoretical foundation for understanding quantum thermodynamic systems. By fundamental assessment and comparison with other quantum approaches, this work opens new avenues for reducing dissipation in quantum systems, with implications for both theoretical research and applied quantum technology.