Universal Learning of Nonlinear Dynamics (2508.11990v1)

Abstract: We study the fundamental problem of learning a marginally stable unknown nonlinear dynamical system. We describe an algorithm for this problem, based on the technique of spectral filtering, which learns a mapping from past observations to the next based on a spectral representation of the system. Using techniques from online convex optimization, we prove vanishing prediction error for any nonlinear dynamical system that has finitely many marginally stable modes, with rates governed by a novel quantitative control-theoretic notion of learnability. The main technical component of our method is a new spectral filtering algorithm for linear dynamical systems, which incorporates past observations and applies to general noisy and marginally stable systems. This significantly generalizes the original spectral filtering algorithm to both asymmetric dynamics as well as incorporating noise correction, and is of independent interest.

• The paper introduces an improper learning framework via the OSF algorithm to predict nonlinear dynamics without explicitly identifying the hidden states.
• It employs spectral filtering and online convex optimization, achieving vanishing regret bounds that scale with Q* and ensuring robustness to noise.
• Empirical evaluations on systems like the Lorenz attractor and double pendulum validate OSF's superior accuracy, scalability, and noise resilience over traditional methods.

Universal Learning of Nonlinear Dynamics: Improper Learning via Spectral Filtering

Introduction and Motivation

The paper "Universal Learning of Nonlinear Dynamics" (2508.11990) presents a rigorous framework for learning and predicting the behavior of nonlinear dynamical systems from observation sequences, without requiring explicit identification of the underlying system dynamics or hidden states. The central innovation is the development of an improper learning algorithm—Observation Spectral Filtering (OSF)—which leverages spectral filtering and online convex optimization to compete against a class of high-dimensional linear observers, rather than attempting to recover the true system. This paradigm shift circumvents the nonconvexity and ill-conditioning inherent in system identification, especially for marginally stable, noisy, and nonlinear systems.

Improper Learning and Comparator Classes

Traditional approaches to learning dynamical systems fall into two categories: model-based system identification (often relying on linear approximations and the Koopman operator) and black-box sequence modeling (e.g., deep learning architectures such as Transformers, SSMs, and convolutional models). Both have limitations: the former is computationally demanding and sensitive to spectral properties, while the latter lacks formal guarantees and interpretability.

The improper learning approach advocated here reframes the prediction task as regret minimization against a tractable comparator class—specifically, the best possible high-dimensional linear observer system for the observed data. This is formalized via the Luenberger observer framework, where the learnability of a system is quantified by a control-theoretic condition number $Q_\star$, derived from an optimization program over observer gains and spectral constraints.

Observation Spectral Filtering (OSF) Algorithm

The OSF algorithm constructs predictions $\hat{y}_{t+1}$ from past observations using a spectral representation. The key steps are:

1. Spectral Filtering: Compute the top eigenpairs of a Hankel matrix formed from the observation history, enabling efficient filtering over temporal patterns.
2. Online Convex Optimization: Update predictor parameters via projected gradient descent or other OCO methods, ensuring vanishing regret against the comparator class.
3. Improper Mapping: Directly map past observations to future predictions, without explicit state estimation or system identification.

The algorithm is parameterized by the number of filters $h$, autoregressive components $m$, and step sizes $\eta_t$, with theoretical guarantees scaling as $O(Q_\star^2 \log(Q_\star) \sqrt{T})$ for $T$ time steps.

Theoretical Guarantees and Control-Theoretic Analysis

The main results establish that OSF achieves vanishing prediction error for any observable nonlinear dynamical system with finitely many marginally stable modes. The regret bounds depend on $Q_\star$, which encapsulates the difficulty of observer design via pole placement and spectral conditioning. Notably:

• No Hidden Dimension Dependence: The algorithm's complexity is independent of the hidden state dimension, a significant advance over prior methods.
• Robustness to Noise and Asymmetry: OSF handles adversarial process noise and asymmetric linear dynamics, generalizing previous spectral filtering techniques.
• Global Linearization via Discretization: Any bounded, Lipschitz nonlinear system can be approximated by a high-dimensional LDS using state-space discretization, enabling the extension of linear guarantees to nonlinear settings.

Empirical Validation

Experiments on synthetic systems, the Lorenz attractor, double pendulum, and Langevin dynamics validate the theoretical predictions. OSF consistently outperforms strong baselines, including eDMD and direct observer learning, in terms of accuracy, robustness, and scaling with $Q_\star$.

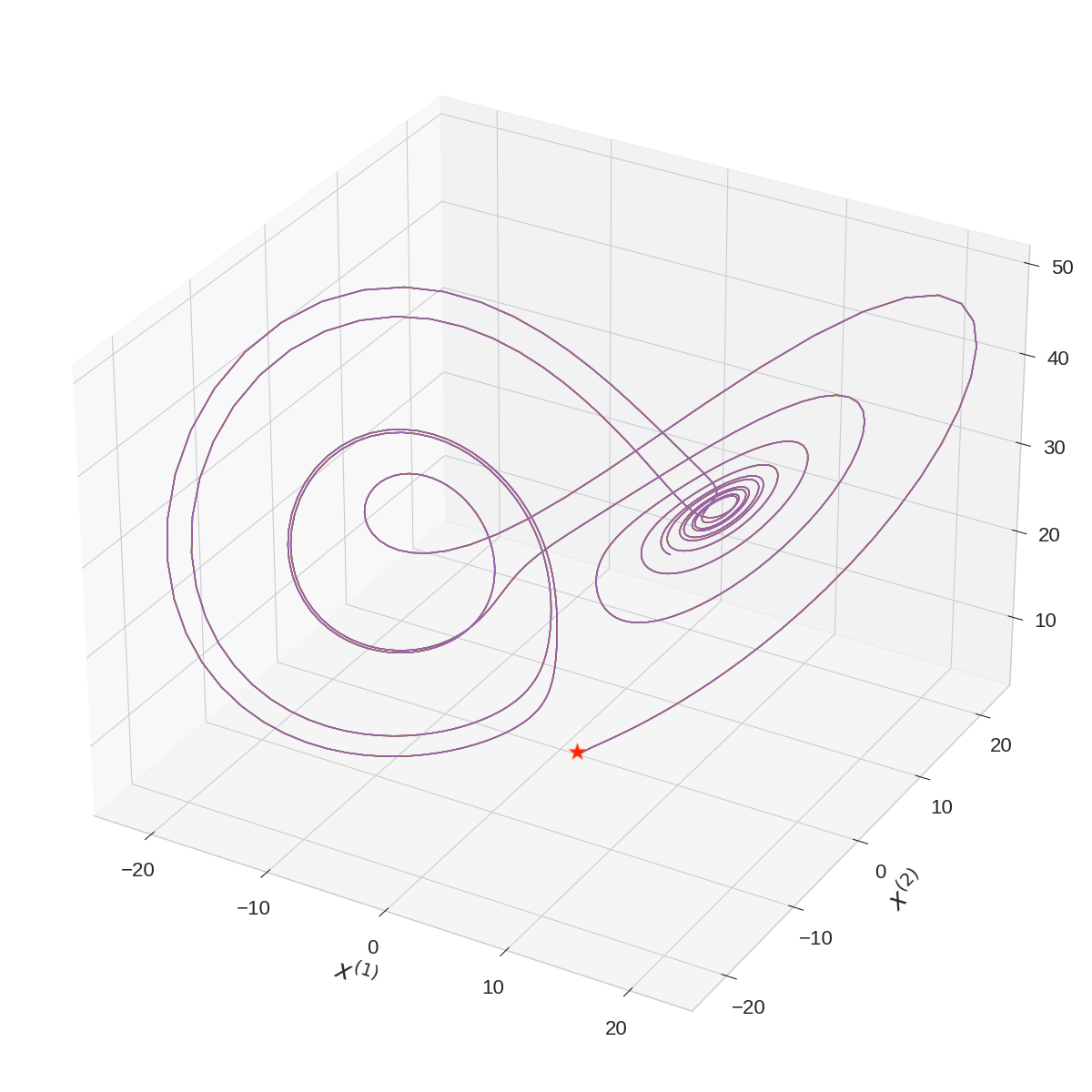
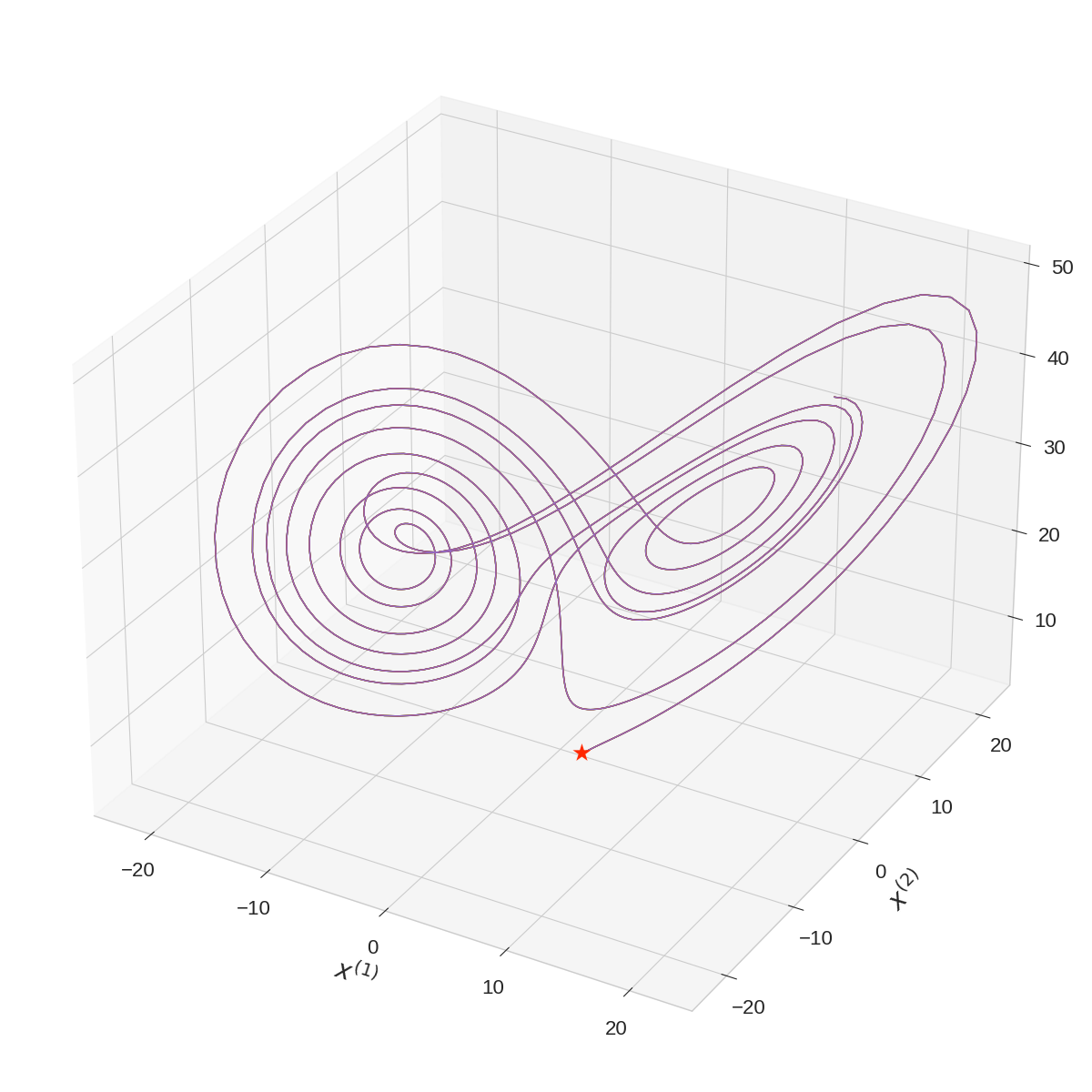
Figure 1: Two trajectories of the Lorenz system, run for 1,024 steps starting from the initial conditions [1, 1, 1] and [1.1, 1, 0.9], respectively. Initial positions are marked with a red star. These two trajectories quickly diverge from each other despite their similar initial conditions, demonstrating the chaotic behavior.

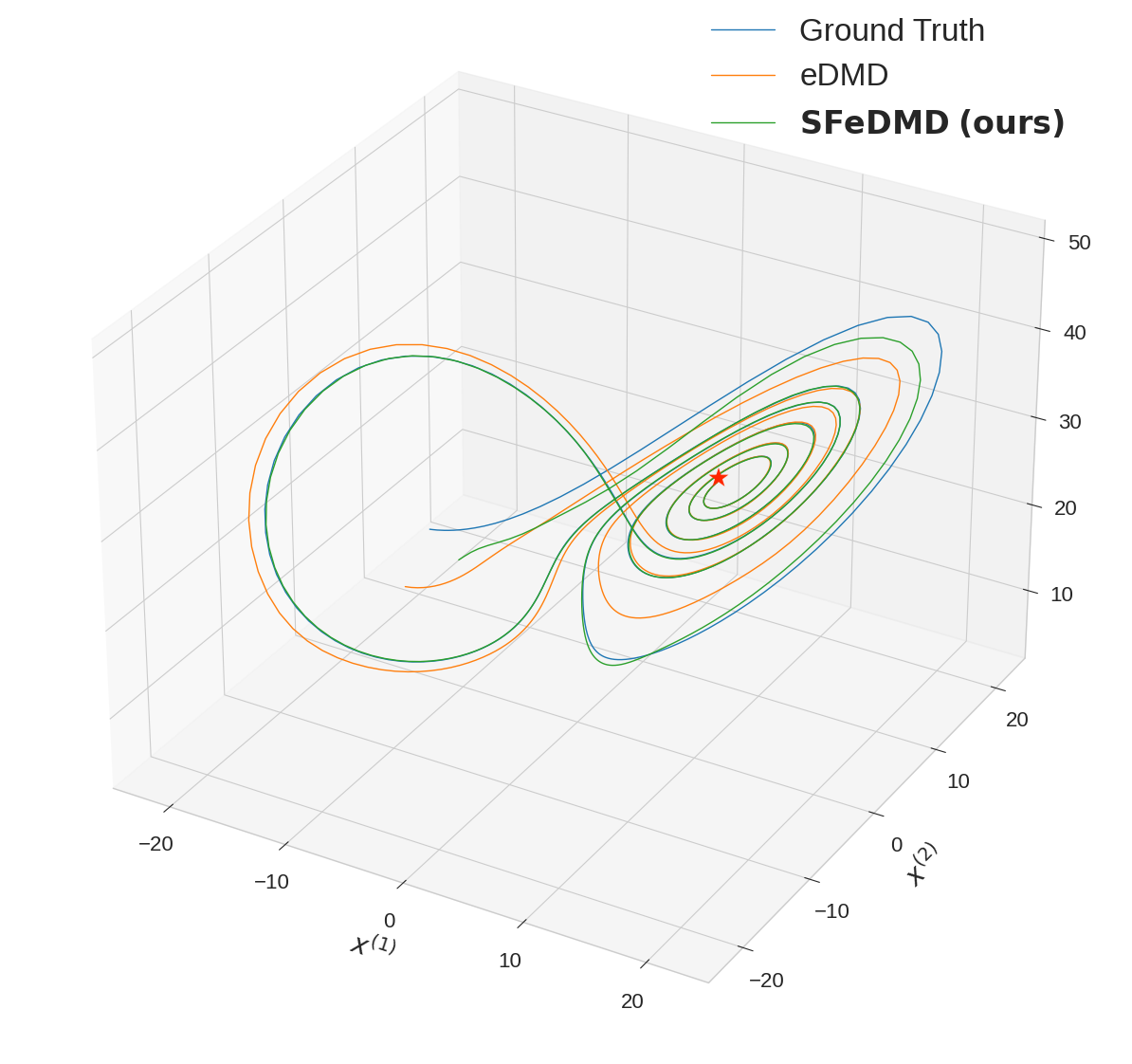
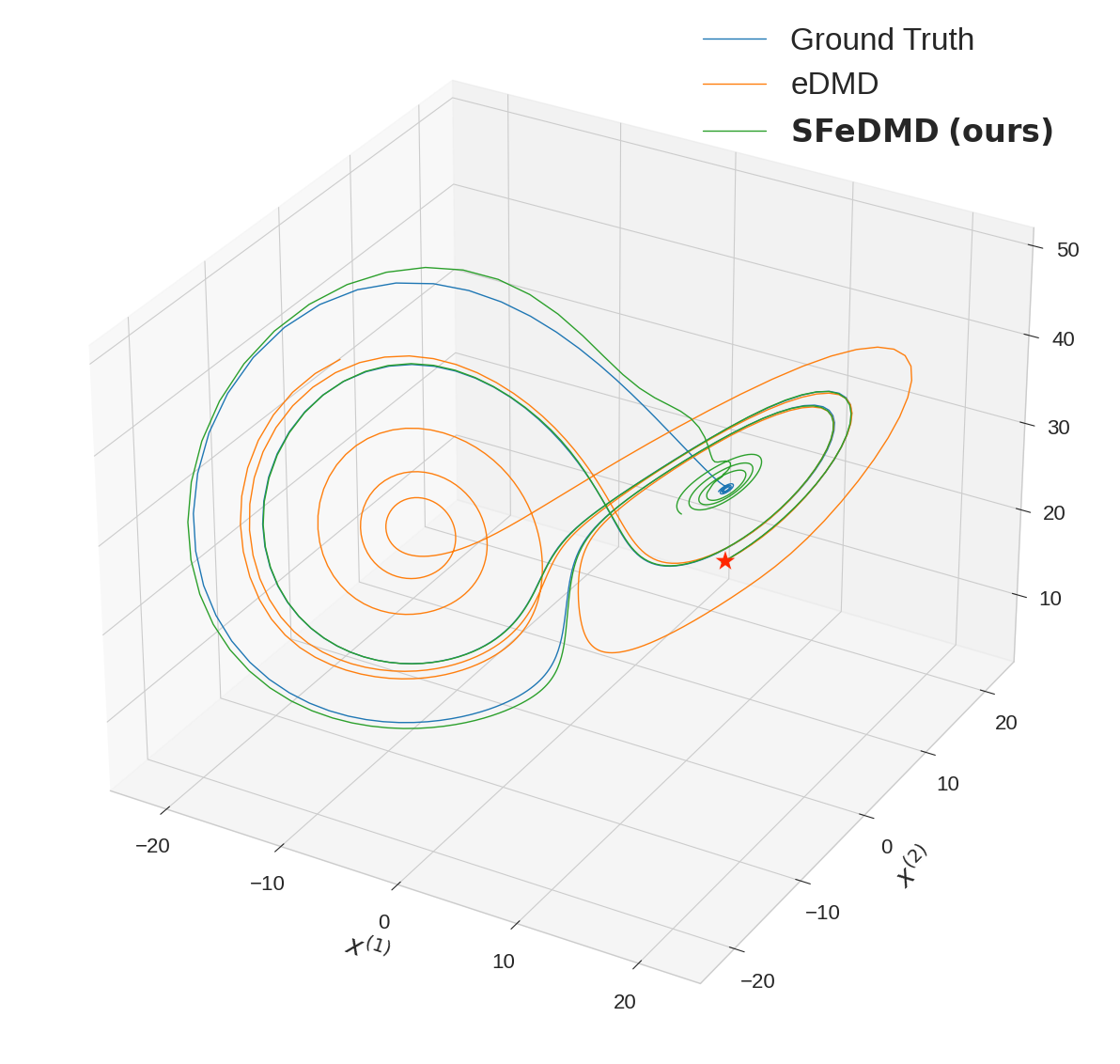
Figure 2: Two sets of autoregressive trajectories of length 512, plotted alongside the ground truth trajectory given by continuing to simulate the Lorenz ODE. The initial positions at which the rollouts start are marked with a red star.

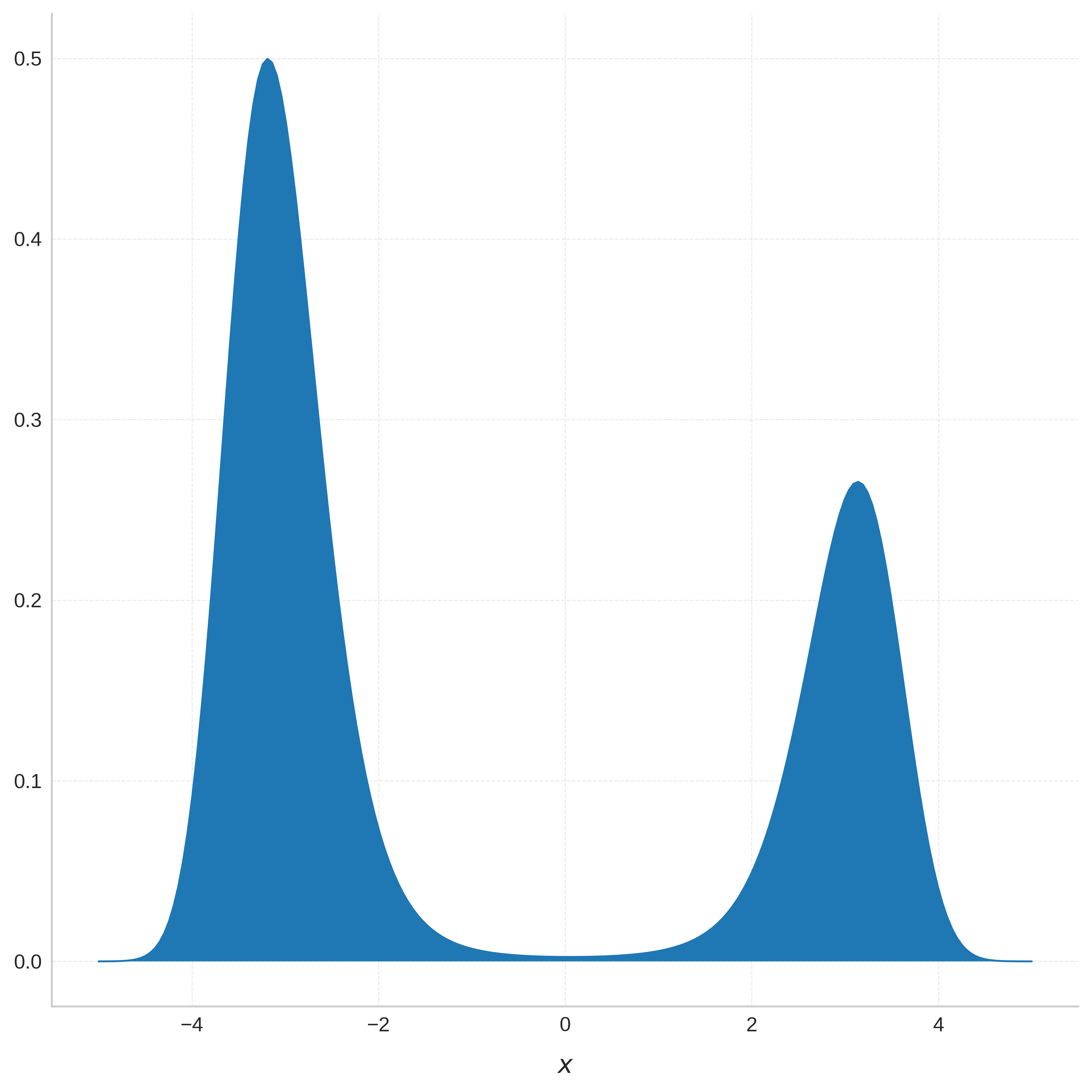
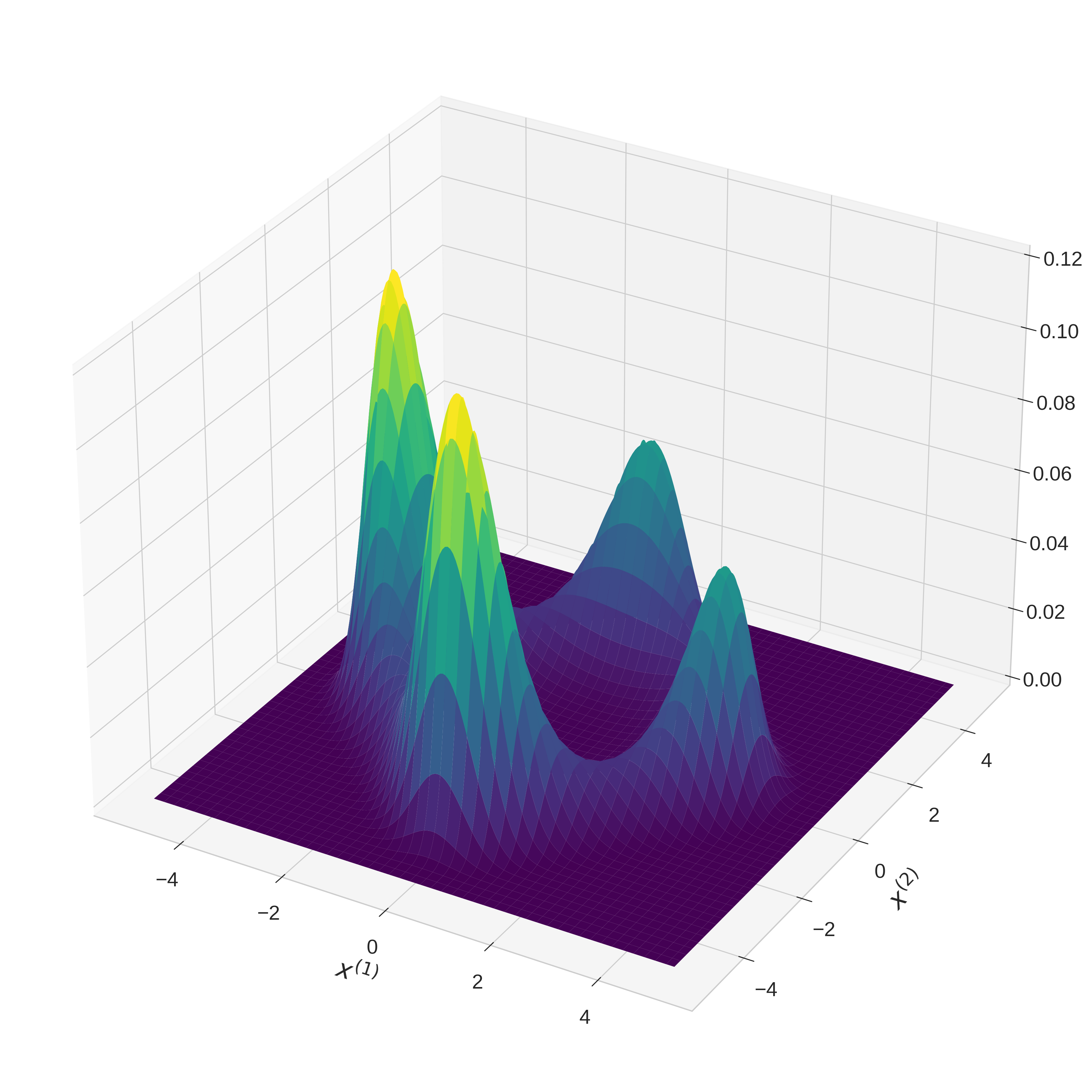
Figure 3: Densities of the stationary distribution $\pi$ corresponding to the chosen potential $V$ for $d_\mathcal{X}$ equal to 1 and 2, respectively. We see a number of asymmetric wells that is exponential in the dimension.

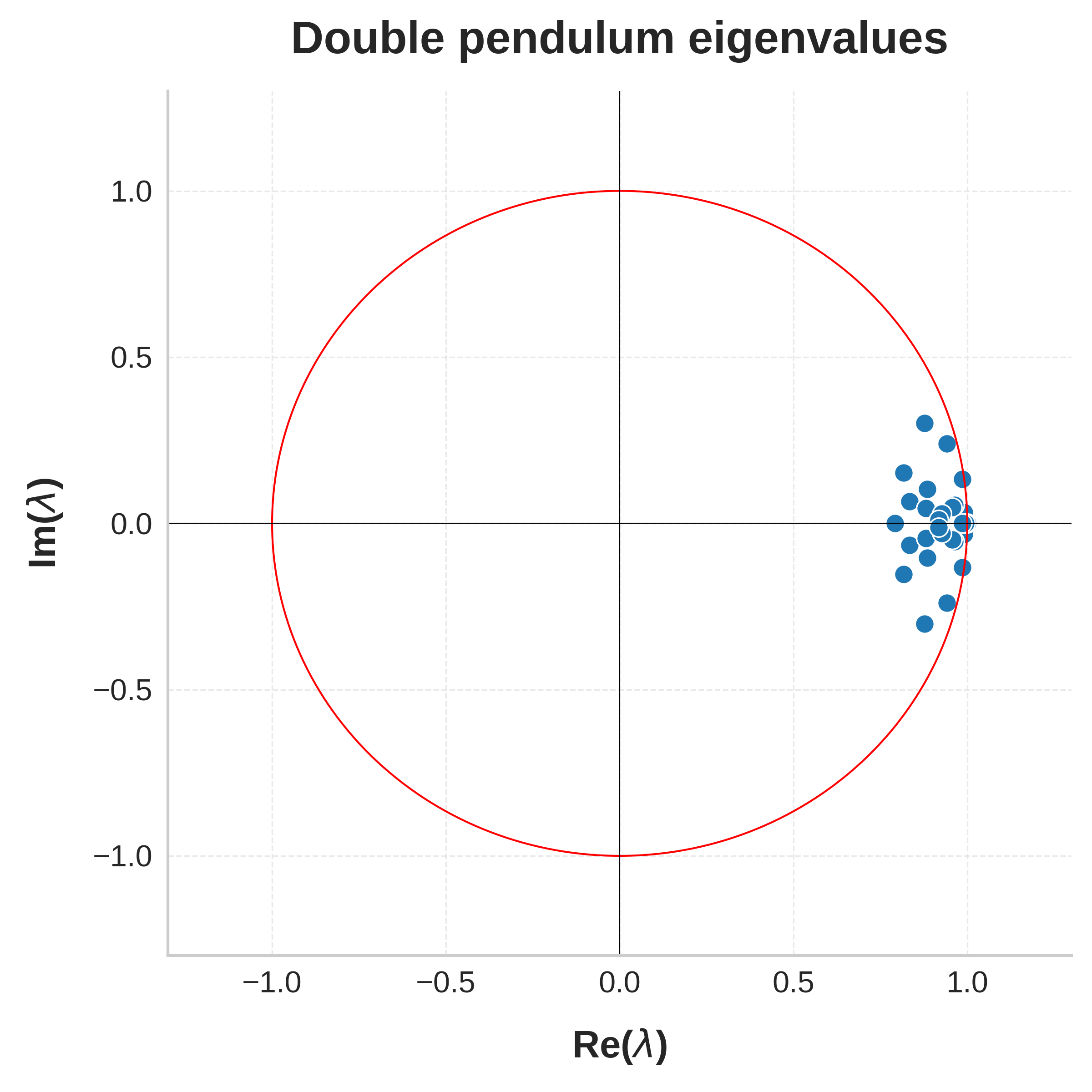
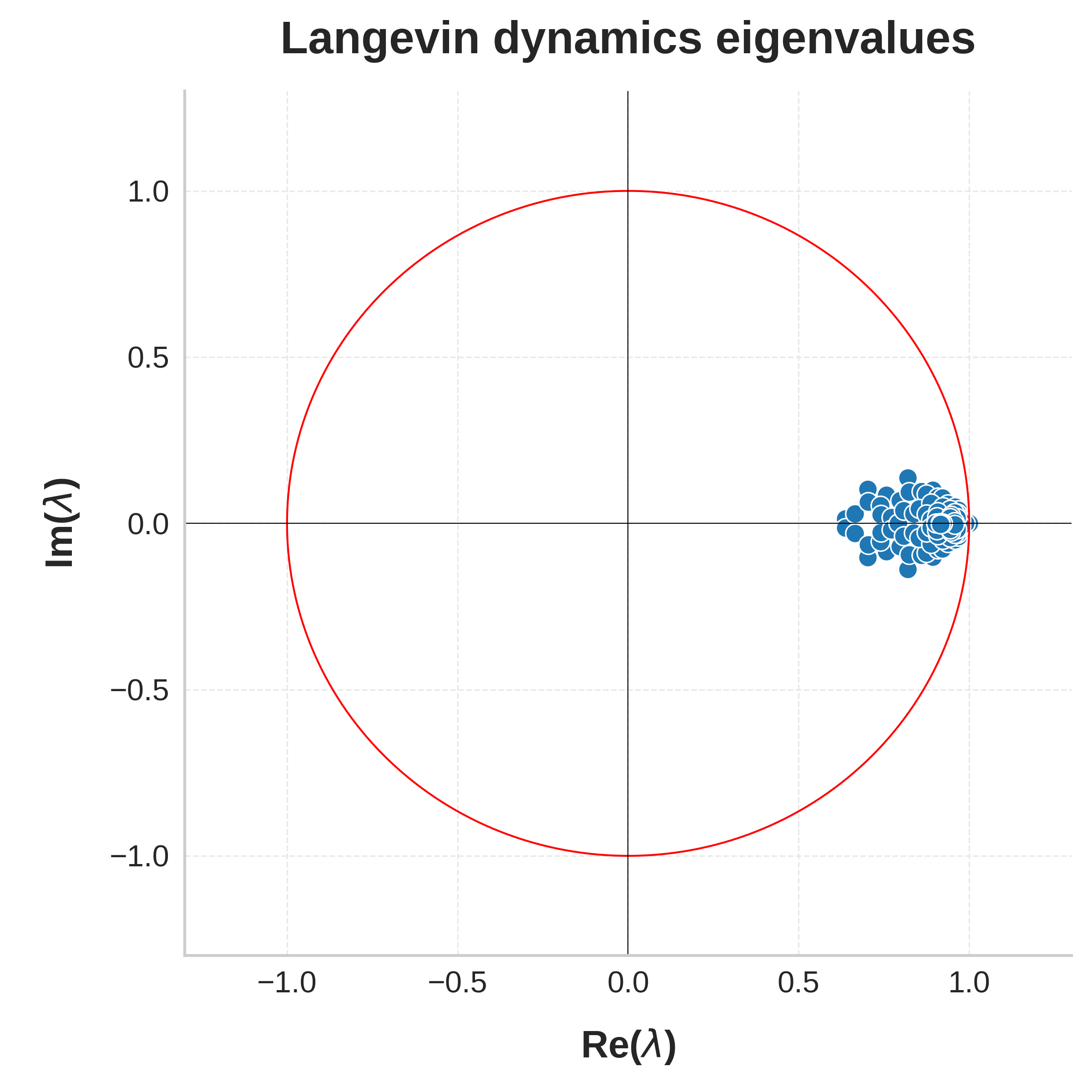
Figure 4: Eigenvalues of the lifted linear dynamics learned by the eDMD algorithm on the Lorenz system, double pendulum, and Langevin dynamics, respectively. The $x$ and $y$ axes display real and complex components, respectively, and we draw the unit circle in red for the reader's convenience.

Trade-offs, Limitations, and Scaling

The regret bounds are optimal in $T$ but can be exponential in the number of undesirable eigenvalues (i.e., those outside the desired spectral region), as captured by $Q_\star$. For systems with real or strongly stable Koopman spectrum, $Q_\star$ is small, yielding efficient learning. However, for highly asymmetric or weakly observable systems, $Q_\star$ may be large, reflecting intrinsic hardness. The discretization-based lifting incurs a dimensionality cost, but OSF's parameterization and runtime remain unaffected.

Practical Implications and Future Directions

The improper learning framework and OSF algorithm have broad implications:

• Provable Learning for Physical Systems: Many physical systems (e.g., Langevin dynamics) have self-adjoint Koopman operators, leading to favorable $Q_\star$ and efficient learnability.
• Universal Applicability: Any nonlinear system with a high-dimensional linear approximation of suitable spectral structure can be learned by OSF.
• Algorithmic Robustness: OSF is robust to noise, partial observability, and nonconvexity, making it suitable for deployment in scientific, engineering, and control applications.

Future work should address the removal of spectral gap assumptions, extension to systems with open-loop inputs, and integration with deep learning architectures for joint nonlinear lifting and spectral filtering. Large-scale empirical studies and theoretical refinements (e.g., sharper dependence on $Q_\star$) are also warranted.

Conclusion

This work establishes a universal, improper learning paradigm for nonlinear dynamical systems, grounded in spectral filtering and control-theoretic analysis. By competing against high-dimensional linear observers and leveraging online convex optimization, OSF achieves provable, efficient, and robust prediction across a wide range of systems. The framework bridges control theory and machine learning, offering new tools for both theoretical analysis and practical sequence modeling in complex dynamical environments.