Optical Interferometric Readout of a Magnetically Levitated Superconducting Microsphere (2508.11731v1)

Abstract: We probe the motion of a 6 $\mu g$ magnetically levitated superconducting microsphere using optical interferometry at 3 K, achieving a resolution better than 1 $nm/ \sqrt{Hz}$, and use the measured signal to feedback-cool its motion. The resolution exceeds the shot-noise limit of 11 $pm/ \sqrt{Hz}$ primarily due to technical noise arising from the roughness of the particle. Combined with established techniques of cavity optomechanics, the high degree of isolation from environmental noise afforded by this platform provides a path to quantum physics experiments with cryogenic isolated masses at the microgram scale.

• The paper presents a novel method for direct optical interferometric readout achieving sub-nanometer displacement sensitivity of a magnetically levitated superconducting microsphere.
• It employs a multi-stage feedback cooling strategy—combining frictional, camera-based, and interferometric techniques—to precisely control the microsphere’s motion at cryogenic temperatures.
• Integration of optical interferometry with superconducting levitation establishes a promising platform for future quantum ground-state cooling experiments and macroscopic quantum tests.

Optical Interferometric Readout of a Magnetically Levitated Superconducting Microsphere

Introduction

This work demonstrates the direct optical interferometric readout and feedback cooling of a magnetically levitated superconducting microsphere at cryogenic temperatures. The experiment achieves sub-nanometer displacement sensitivity, exceeding the photon shot-noise limit, and establishes a platform for quantum optomechanics with microgram-scale masses. The integration of optical interferometry with superconducting levitation addresses a longstanding challenge in the field, enabling high-precision measurement and control of massive, isolated mechanical oscillators.

Experimental Platform and Methodology

The core of the experiment is a $\SI{6}{\micro\gram}$ PbSn superconducting sphere, magnetically levitated in an anti-Helmholtz trap at $\SI{3}{\kelvin}$. The trap is formed by NbTi coils, providing a dissipationless and highly isolated environment. The mechanical frequencies of the levitated particle are tunable via the trap current, with axial and radial modes accessible for measurement and control.

Optical interferometry is implemented along the axial direction using a Mach-Zehnder-like configuration with a $\SI{637}{\nano\meter}$ laser. The sphere acts as a moving mirror, and balanced homodyne detection is employed to extract both phase (axial displacement) and intensity (radial displacement) information. The interferometric signal is linearized over a large dynamic range using a high-gain closed-loop feedback with an acousto-optic modulator (AOM), enabling accurate tracking of the particle's motion even for amplitudes exceeding $\lambda/8$.

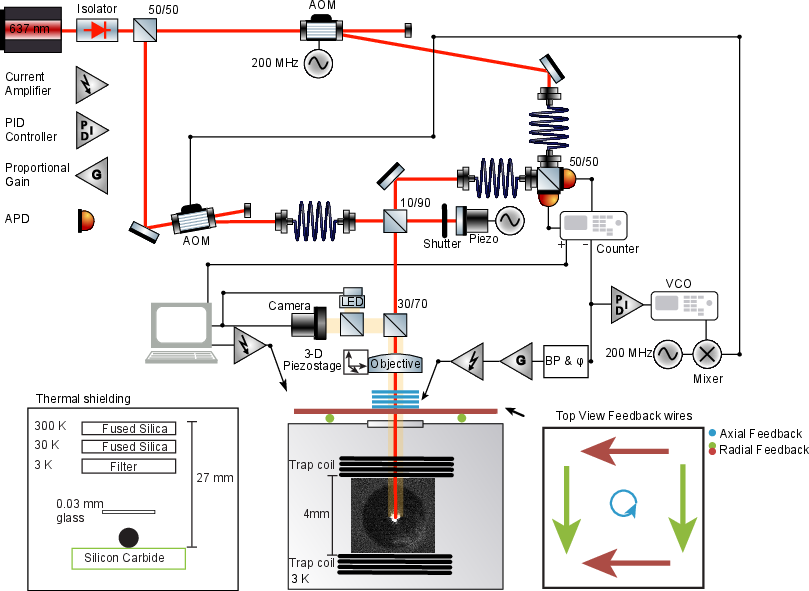
Figure 2: Schematic of the experimental setup, showing the magnetic trap, optical interferometer, and feedback control architecture.

The experimental sequence involves several cooling stages. Initially, frictional cooling is achieved by controlled contact with the SiC substrate. Subsequent camera-based feedback reduces radial motion, followed by intensity-based feedback using the reflected laser signal. Finally, interferometric feedback is applied to the axial mode, achieving the lowest motional amplitudes.

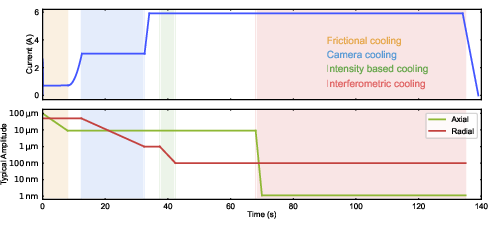
Figure 4: Typical experimental sequence, illustrating the progression from frictional cooling to interferometric feedback.

Calibration and Sensitivity

Absolute calibration of the interferometric readout is performed via two independent methods: (1) applying a known oscillatory force to the particle using an external coil, and (2) driving a piezo-mounted mirror with a known amplitude. Both approaches yield consistent results, confirming the accuracy of the displacement measurement.

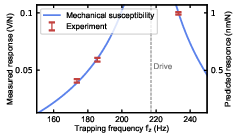
Figure 5: Calibration of the interferometer signal using an oscillating magnetic force at different trap frequencies.

The measured displacement noise floor is $\sqrt{2\,S_{zz}} = \SI{955\pm148}{\pico\meter/\sqrt{\hertz}}$, which is two orders of magnitude above the photon shot-noise limit ($\SI{11}{\pico\meter/\sqrt{\hertz}}$ for the given photon flux). The excess noise is attributed to technical sources, primarily the surface roughness and rotational dynamics of the microsphere.

Feedback Cooling Performance

Feedback cooling is implemented by bandpass filtering the interferometric signal around the mechanical resonance and applying a phase-shifted current to the feedback coils. The system achieves a minimum cooled displacement amplitude of $\sqrt{\langle z^2 \rangle_\mathrm{min}} \approx \SI{8}{\nano\meter}$, corresponding to a phonon occupation $\Bar{n}\approx 5\times10^{12}$ and an effective temperature of $\SI{52e3}{K}$.

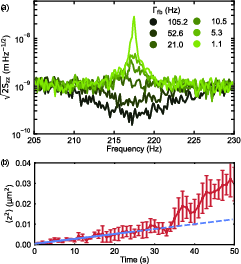
Figure 6: (a) Power spectral density of displacement noise for varying feedback gains; (b) Ring-up of motional energy after cooling, used to extract the thermal decoherence rate.

Optimal feedback gain yields a flat spectral density, with higher gains leading to classical noise squashing below the measurement noise floor. The observed thermal decoherence rate is $\Gamma_\mathrm{th} = \SI{6.4e12}{Hz}$ at a trap frequency of $\SI{160}{Hz}$. The quantum cooperativity, defined as $$\mathcal{C}_\mathrm{q} = \Gamma_\mathrm{ba}/\Gamma_\mathrm{th}$$, is $\sim 1.4\times10^{-21}$, far from the regime required for quantum ground-state cooling.

Technical Limitations and Noise Sources

The dominant limitation in displacement sensitivity arises from the surface roughness and asphericity of the commercial PbSn spheres, as confirmed by microscopy and white-light interferometry. Rotational and librational modes further contribute to technical noise, especially at higher photon fluxes. The superconducting state is robust against the applied optical power for experimental timescales up to $\SI{100}{\second}$, but higher fluxes or longer durations induce quenching due to heating and quasiparticle generation.

Pathways to Quantum Ground-State Cooling

Theoretical analysis shows that, even with perfect detection efficiency and the measured mechanical quality factor ($Q=2.6\times10^7$), direct free-space interferometric readout would require an unfeasibly high photon flux ($\sim 7.5\times10^{17}\,\mathrm{photons/s}$, or $\SI{235}{\milli\watt}$) to reach the quantum ground state, due to the shot-noise constraint. This would result in excessive heating and loss of superconductivity.

Integration of a high-finesse optical cavity, with the levitated sphere as one mirror, can enhance the optomechanical coupling and reduce the required photon flux by several orders of magnitude. For a cavity with finesse $\mathcal{F}=10^5$, $\lambda=1.55\,\mu$m, and $\eta=0.75$, ground-state cooling is achievable with only $n_\mathrm{in}=\SI{7E6}{\mathrm{photons/s}}$ ($\SI{0.9}{\pico\watt}$) at $T=\SI{15}{\milli\kelvin}$.

Advanced Cooling and Control Protocols

The experiment demonstrates a multi-stage feedback protocol, combining frictional, camera-based, intensity-based, and interferometric cooling. Camera-based feedback reduces radial motion from tens of micrometers to sub-micrometer levels, while intensity-based feedback further damps the motion to $\sim 100$ nm. The interferometric feedback on the axial mode achieves the highest precision.

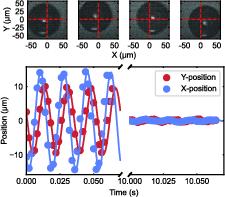
Figure 8: Camera-based feedback cooling reduces radial motion from tens of micrometers to below $1\,\mu$m.

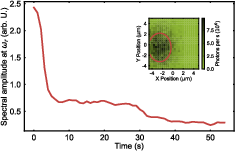
Figure 10: Intensity-based feedback cooling of the radial mode, showing reduction of amplitude over time.

Implications and Future Directions

This work establishes the feasibility of direct optical readout and feedback control of magnetically levitated superconducting microspheres at cryogenic temperatures. The demonstrated sensitivity and isolation are sufficient for a range of precision measurements and foundational tests in macroscopic quantum mechanics. However, technical noise from particle imperfections and the limitations of free-space detection preclude immediate access to the quantum regime.

The integration of high-finesse optical cavities, improved particle fabrication (e.g., monocrystalline or polished spheres), and operation at lower temperatures ($\sim$ mK) are clear next steps. These advances would enable quantum-limited measurement and control, opening the door to experiments probing gravitational quantum effects, macroscopic entanglement, and tests of collapse models.

Conclusion

The direct optical interferometric readout of a magnetically levitated superconducting microsphere at $\SI{3}{\kelvin}$ achieves sub-nanometer sensitivity and effective feedback cooling, establishing a new platform for macroscopic quantum optomechanics. While technical noise currently limits access to the quantum regime, the integration of cavity-enhanced detection and improved particle quality offers a viable path to ground-state cooling and quantum control of microgram-scale levitated objects. This platform is poised to play a significant role in future explorations of quantum mechanics at unprecedented mass and length scales.