Noise Hypernetworks: Amortizing Test-Time Compute in Diffusion Models (2508.09968v1)

Abstract: The new paradigm of test-time scaling has yielded remarkable breakthroughs in LLMs (e.g. reasoning models) and in generative vision models, allowing models to allocate additional computation during inference to effectively tackle increasingly complex problems. Despite the improvements of this approach, an important limitation emerges: the substantial increase in computation time makes the process slow and impractical for many applications. Given the success of this paradigm and its growing usage, we seek to preserve its benefits while eschewing the inference overhead. In this work we propose one solution to the critical problem of integrating test-time scaling knowledge into a model during post-training. Specifically, we replace reward guided test-time noise optimization in diffusion models with a Noise Hypernetwork that modulates initial input noise. We propose a theoretically grounded framework for learning this reward-tilted distribution for distilled generators, through a tractable noise-space objective that maintains fidelity to the base model while optimizing for desired characteristics. We show that our approach recovers a substantial portion of the quality gains from explicit test-time optimization at a fraction of the computational cost. Code is available at https://github.com/ExplainableML/HyperNoise

• The paper introduces a noise hypernetwork that amortizes test-time noise optimization using a lightweight, LoRA-adapted module.
• It employs KL-regularized reward maximization to predict improved noise patterns while maintaining fidelity to the base distribution.
• Empirical results demonstrate significant gains in prompt fidelity and image quality with drastically reduced inference overhead.

Noise Hypernetworks: Amortizing Test-Time Compute in Diffusion Models

Introduction and Motivation

Test-time scaling—allocating additional computation at inference to improve generative model outputs—has become a standard paradigm in both LLMs and diffusion-based vision models. In diffusion models, this often takes the form of per-sample optimization of the initial noise or intermediate latents, guided by reward models that measure prompt faithfulness, aesthetics, or other desired properties. While effective, these methods are computationally expensive, incurring significant latency and memory overhead, which limits their practical deployment, especially in real-time or large-scale settings.

The paper introduces Noise Hypernetworks (HyperNoise), a framework that amortizes the benefits of test-time noise optimization into a lightweight, post-training module. Instead of optimizing the initial noise for each sample at inference, a small hypernetwork is trained to predict an improved noise initialization, conditioned on the same random seed and prompt, which is then used by a frozen, distilled diffusion generator. This approach aims to recover much of the quality gains of explicit test-time optimization, but with negligible additional inference cost.

Figure 1: HyperNoise significantly improves prompt faithfulness and aesthetic quality over the base generation for both SANA-Sprint and FLUX-Schnell, using the same initial random noise.

Theoretical Framework

Reward-Tilted Distributions and the Challenge of Direct Fine-Tuning

The goal is to align the output distribution of a pre-trained, distilled diffusion model $g_\theta$ with a reward function $r(\cdot)$, yielding a reward-tilted distribution:

$p^\star(x) \propto p^{\text{base}}(x) \exp(r(x))$

where $p^{\text{base}}$ is the pushforward of the standard Gaussian noise prior through $g_\theta$. Directly fine-tuning $g_\theta$ to match $p^\star$ is theoretically sound but practically infeasible for distilled models, as the KL regularization term between the new and base output distributions is intractable due to the lack of explicit density models and the high dimensionality of the data space.

Noise Hypernetworks: Modulating the Initial Noise

HyperNoise circumvents this by learning a transformation $T_\phi$ (parameterized by a hypernetwork $f_\phi$) that maps standard Gaussian noise $\epsilon_0$ to a modulated noise $\hat{\epsilon}_0 = \epsilon_0 + f_\phi(\epsilon_0)$. The frozen generator $g_\theta$ then maps $\hat{\epsilon}_0$ to the output space. The key insight is that the optimal modulated noise distribution $p_0^\star$ that induces $p^\star$ through $g_\theta$ is:

$$p_0^\star(\epsilon_0) \propto p_0(\epsilon_0) \exp(r(g_\theta(\epsilon_0)))$$

The training objective for $f_\phi$ is to minimize the KL divergence between the modulated and standard noise distributions, regularized by the reward:

$$\mathcal{L}_{\text{noise}}(\phi) = D_{\text{KL}}(p_0^\phi \| p_0) - \mathbb{E}_{\hat{\epsilon}_0 \sim p_0^\phi}[r(g_\theta(\hat{\epsilon}_0))]$$

This KL term is tractable in noise space and, under mild Lipschitz assumptions, can be well-approximated by an $L_2$ penalty on the magnitude of $f_\phi(\epsilon_0)$.

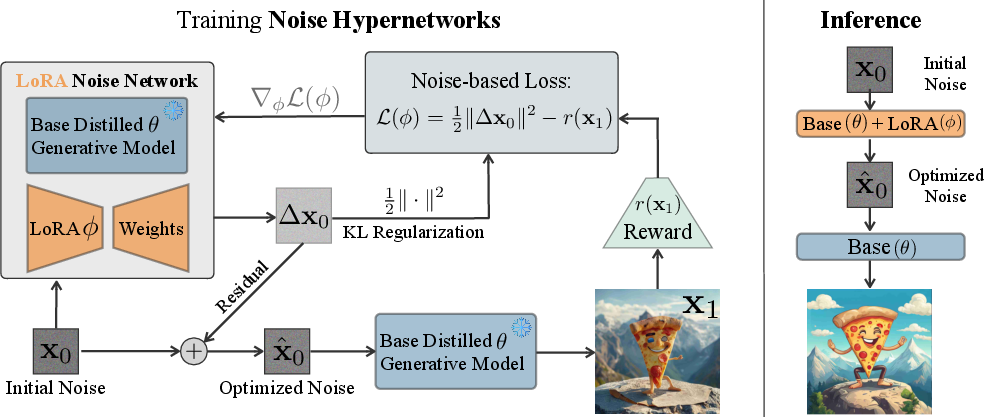
Figure 2: Schematic of HyperNoise. During training, LoRA parameters are optimized to predict improved noises via reward maximization and KL regularization. At inference, the hypernetwork predicts the improved noise in a single step.

Implementation Details

LoRA-based Hypernetwork

The noise hypernetwork $f_\phi$ is implemented as a LoRA-adapted copy of the base generator $g_\theta$, with only the LoRA weights trainable. This ensures parameter efficiency and minimal memory overhead, as the base model is kept frozen and only the small set of LoRA parameters are updated. Initialization is set such that $f_\phi(\cdot) = 0$ at the start of training, ensuring stability and that the initial modulated noise matches the standard Gaussian.

Training Procedure

• Inputs: Standard Gaussian noise samples, the frozen generator, and a reward function (possibly an ensemble of reward models).
• Objective: Minimize the $L_2$-regularized reward maximization loss.
• Optimization: SGD or AdamW, with gradient norm clipping and batch sizes tuned for available hardware.
• Inference: A single forward pass through $f_\phi$ and $g_\theta$ suffices, with negligible additional latency compared to the base model.

Empirical Results

Redness Reward: Controlled Illustration

A controlled experiment with a simple "redness" reward demonstrates that direct fine-tuning of the generator can lead to reward hacking and divergence from the data manifold, manifesting as low-quality or unrealistic images. In contrast, HyperNoise achieves high reward while maintaining fidelity to the base distribution, as measured by both the reward and a human-preference image quality metric.

Figure 3: Comparison of direct LoRA fine-tuning and HyperNoise on a redness reward. HyperNoise optimizes the reward while staying close to the base image manifold.

Human-Preference Alignment: Large-Scale Evaluation

HyperNoise is evaluated on state-of-the-art distilled diffusion models (SD-Turbo, SANA-Sprint, FLUX-Schnell) using human-preference reward models (ImageReward, HPSv2.1, PickScore, CLIP-Score). On the GenEval benchmark, HyperNoise consistently improves prompt faithfulness, compositionality, and overall image quality, recovering a substantial fraction of the gains from explicit test-time optimization (e.g., ReNO, Best-of-N, LLM-based prompt optimization) but at a fraction of the inference cost.

• SD-Turbo: GenEval mean improves from 0.49 to 0.57, surpassing SDXL (2x parameters, 25x NFEs).
• SANA-Sprint: Improves from 0.70 to 0.75, matching LLM-based prompt optimization but 300x faster.
• FLUX-Schnell: Improves from 0.68 to 0.72, with similar efficiency gains.

  Figure 4: Qualitative comparison of HyperNoise with distilled models for 4-step generation. HyperNoise consistently improves prompt adherence and visual quality.

Robustness and Generalization

HyperNoise generalizes across different numbers of inference steps, even when trained only for one-step generation. It consistently outperforms direct fine-tuning, which often leads to reward hacking and degraded image quality.

Figure 5: Artifacts introduced by direct fine-tuning on rewards, compared to HyperNoise which avoids such issues.

Qualitative Analysis

HyperNoise yields visually superior generations, with improved prompt following, compositionality, and fewer artifacts, as confirmed by both cherry-picked and non-cherry-picked samples.

Figure 6: More qualitative results on the human-preference reward setting. HyperNoise improves over the base SANA-Sprint for the same initial noise.

Figure 7: Non-cherry picked results on the human-preference reward setting. HyperNoise consistently improves over the base model.

Discussion and Implications

Theoretical and Practical Impact

HyperNoise provides a theoretically grounded and computationally efficient solution for aligning distilled diffusion models with arbitrary reward functions. By shifting the optimization from per-sample inference to a one-time post-training phase, it enables high-quality, reward-aligned generation at scale, with minimal inference overhead. The approach is particularly well-suited for real-time and large-scale applications where test-time optimization is prohibitive.

Limitations

The method relies on the quality of the base model and the reward function. If the reward model is misaligned with human preferences or the base generator is weak, improvements may be limited. The approach is also constrained by the expressivity of the noise hypernetwork and the LoRA adaptation.

Future Directions

• Reward Model Improvements: As reward models become more robust and better aligned with human preferences, HyperNoise can leverage these advances for further gains.
• Extension to Other Modalities: The framework is general and could be applied to other generative domains (e.g., audio, video, text).
• Adaptive and Conditional Hypernetworks: Exploring more expressive or conditional hypernetwork architectures could further enhance alignment and generalization.

Conclusion

Noise Hypernetworks offer a principled, efficient, and practical approach to distilling the benefits of test-time optimization into a lightweight, post-training module for diffusion models. The method achieves substantial improvements in prompt faithfulness and image quality across multiple state-of-the-art distilled models, with negligible inference cost and without the pitfalls of reward hacking. This framework provides a scalable path for aligning generative models with complex, downstream objectives in real-world deployments.