$μ$-Parametrization for Mixture of Experts (2508.09752v1)

Abstract: Recent years have seen a growing interest and adoption of LLMs, with $\mu$Transfer becoming a key technique for tuning hyperparameters in large-scale training. Meanwhile, Mixture-of-Experts (MoE) has emerged as a leading architecture in extremely large models. However, the intersection of these two advancements has remained unexplored. In this work, we derive a $\mu$-Parameterization ($\mu$P) for MoE, providing theoretical guarantees for feature learning across model widths in both the router and experts. We empirically validate our parameterization and further investigate how scaling the number of experts and granularity affects the optimal learning rate.

• The paper presents a principled derivation of μP for MoE, offering formal guarantees for feature learning and consistent parameter scaling.
• Empirical results demonstrate that μP enables learning rate transfer across model widths and expert counts while highlighting limitations in granularity scaling.
• The study provides actionable insights for reducing hyperparameter tuning costs in large sparse models, paving the way for efficient training of MoE architectures.

μ-Parametrization for Mixture of Experts: Theory and Empirical Analysis

Introduction

The paper presents a principled extension of Maximal Update Parameterization (μP) to Mixture-of-Experts (MoE) architectures, addressing a critical gap in the scaling and hyperparameter transferability of large sparse models. While μP has enabled robust hyperparameter transfer in dense architectures, its application to MoE—where routing and expert sparsity introduce new scaling challenges—has remained theoretically unresolved. This work rigorously derives μP for MoE, provides formal guarantees for feature learning across model widths, and empirically validates the transferability of learning rates under this new parameterization. The analysis further explores the boundaries of hyperparameter transfer when scaling other MoE dimensions, such as the number of experts and granularity.

Theoretical Framework: μP for MoE

The derivation of μP for MoE builds on Tensor Programs V (TP5) and the distinction between hidden and output weights. In MoE, expert weights map infinite to infinite dimensions and are treated as hidden weights, while the router maps infinite to finite dimensions and is treated as an output weight. The paper formalizes the scaling of activations and gradients to ensure that:

• Hidden representations and output logits are $O(1)$ at initialization.
• Updates to hidden states and logits after one optimization step are $O(1)$, independent of model width.

This scaling is achieved by initializing expert weights with variance $1/\text{fan\_in}$ and router weights with variance $1.0$, and by applying learning rates scaled as $1/\text{fan\_in}$ for experts and $1.0$ for the router. The covariance lemma in the appendix rigorously proves that the forward activations of experts and their backward gradients remain correlated at order $\Theta(1/n)$, and that the router’s gradient norm is $\Theta(1)$, both at initialization and after one μP-SGD/Adam update.

Empirical Validation: Learning Rate Transfer Across Model Widths

The empirical section demonstrates that μP enables robust learning rate transfer across model widths in MoE architectures. Three parameterizations are compared:

• Standard Parameterization (SP): No scaling, resulting in different optimal learning rates for different model sizes.
• simpleP-MoE: Treats each expert as a dense MLP, applying μP only to experts.
• μP-MoE: Applies the full μP theory to both experts and router.

Both simpleP-MoE and μP-MoE achieve learning rate transfer, with optimal learning rates remaining stable across model widths, in contrast to SP.

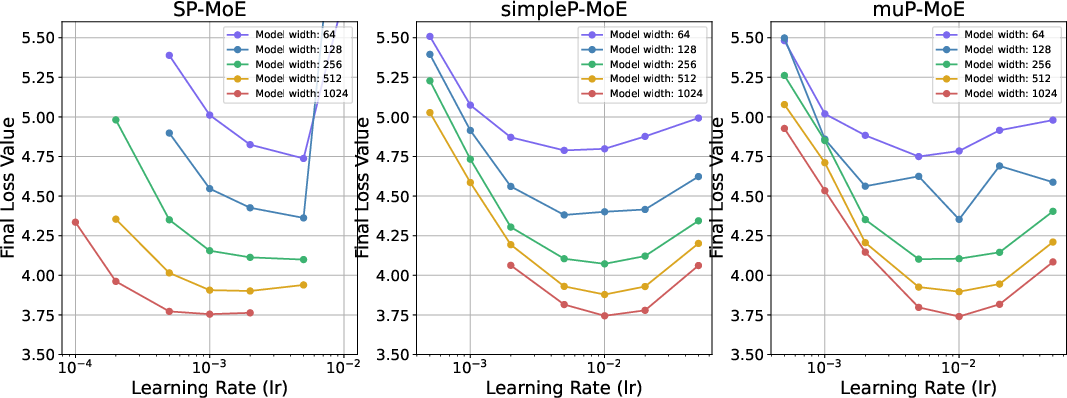
Figure 1: MoE performance for varying learning rates and model widths; μP and simpleP parameterizations enable learning rate transfer, while SP does not.

The experiments also note a slight upward shift in optimal learning rate for wider models, consistent with prior TP5 results and possibly attributable to depth-to-width ratio instabilities. Notably, two μP-MoE runs with embedding dimension 128 diverged, suggesting potential stability issues that warrant further investigation.

Scaling Other MoE Dimensions: Experts and Granularity

The analysis extends to other MoE scaling parameters:

• Number of Experts: Increasing the number of experts improves final loss without affecting computational cost. Under μP, the optimal learning rate is preserved across different numbers of experts.

(Figure 2a)

Figure 2: (a) Learning rate transfer is preserved when varying the number of experts under μP.

• Granularity: Adjusting granularity (i.e., reducing expert hidden size and increasing the number of experts and top-$k$) breaks learning rate transferability. The optimal learning rate does not transfer between granularities, likely due to changes in router output dimension and top-$k$ selection.

(Figure 2b)

Figure 2: (b) Learning rate transfer fails across different granularities, indicating a boundary of μP theory in MoE.

These results highlight that while μP robustly supports scaling in model width and number of experts, it does not generalize to granularity scaling without further theoretical adaptation.

Comparison to Dense Models

For completeness, the paper verifies μP in dense Transformers, reproducing the result that optimal learning rates transfer across model widths, whereas SP does not.

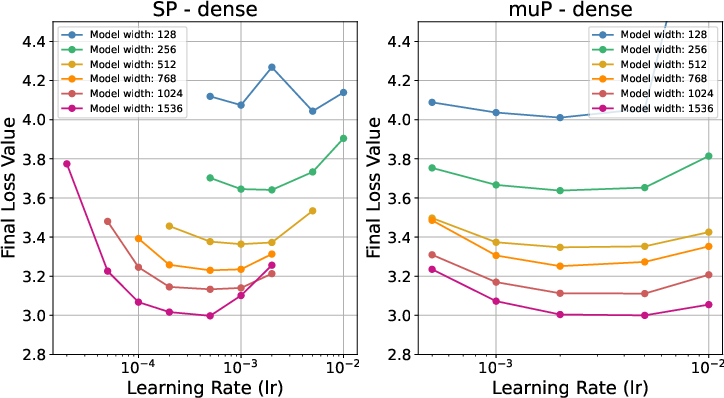
Figure 3: Learning rate transfer in dense models; μP yields stable optima across widths, SP does not.

Implementation Considerations

Parameterization

• Expert Weights: Initialize with variance $1/\text{fan\_in}$, learning rate scaled as $1/\text{fan\_in}$.
• Router Weights: Initialize with variance $1.0$, learning rate $1.0$.
• Optimizer: AdamW with cosine decay and linear warmup.
• Precision: Mixed precision training, high precision for attention.
• Auxiliary Losses: z-loss and load balancing for router stability.

Scaling and Transfer

• Hyperparameters tuned on small models can be transferred to larger models under μP, reducing tuning cost and computational overhead.
• Scaling the number of experts is supported; scaling granularity is not, due to theoretical limitations in current μP.

Stability

• Potential instability in μP-MoE for small embedding dimensions; further empirical and theoretical work is needed.

Implications and Future Directions

The extension of μP to MoE architectures provides a formal foundation for hyperparameter transfer in large sparse models, facilitating efficient scaling and reducing the cost of hyperparameter search. The empirical results confirm the theoretical predictions for model width and number of experts, but reveal limitations when scaling granularity. This boundary suggests that further generalization of μP theory is required to fully support fine-grained MoE architectures and top-$k$ scaling.

Practically, the results enable more predictable and stable training of large MoE models, supporting the deployment of trillion-parameter LLMs with reduced engineering overhead. Theoretically, the work motivates new research into parameterization schemes that can accommodate the full spectrum of MoE scaling strategies, including granularity and dynamic routing.

Conclusion

This paper rigorously derives and empirically validates μ-Parametrization for Mixture-of-Experts, enabling robust hyperparameter transfer across model widths and number of experts. The findings delineate the boundaries of current μP theory, showing that granularity scaling disrupts learning rate transferability. Future work should address the theoretical challenges posed by granularity and top-$k$ scaling, further advancing the scalability and efficiency of sparse large models.