Sample More to Think Less: Group Filtered Policy Optimization for Concise Reasoning (2508.09726v1)

Abstract: LLMs trained with reinforcement learning with verifiable rewards tend to trade accuracy for length--inflating response lengths to achieve gains in accuracy. While longer answers may be warranted for harder problems, many tokens are merely "filler": repetitive, verbose text that makes no real progress. We introduce GFPO (Group Filtered Policy Optimization), which curbs this length explosion by sampling larger groups per problem during training and filtering responses to train on based on two key metrics: (1) response length and (2) token efficiency: reward per token ratio. By sampling more at training time, we teach models to think less at inference time. On the Phi-4-reasoning model, GFPO cuts GRPO's length inflation by 46-71% across challenging STEM and coding benchmarks (AIME 24/25, GPQA, Omni-MATH, LiveCodeBench) while maintaining accuracy. Optimizing for reward per token further increases reductions in length inflation to 71-85%. We also propose Adaptive Difficulty GFPO, which dynamically allocates more training resources to harder problems based on real-time difficulty estimates, improving the balance between computational efficiency and accuracy especially on difficult questions. GFPO demonstrates that increased training-time compute directly translates to reduced test-time compute--a simple yet effective trade-off for efficient reasoning.

• The paper introduces GFPO, which curbs excessive verbosity in RL-trained LLMs by selectively learning from top candidate responses.
• It employs group-based sampling with metrics like token efficiency to achieve up to 84.6% reduction in response length without losing accuracy.
• Experimental results demonstrate GFPO's Pareto superiority over GRPO, maintaining reasoning quality while significantly reducing inference compute.

Group Filtered Policy Optimization: Concise Reasoning via Selective Training

Introduction and Motivation

Reinforcement learning from verifier rewards (RLVR) has enabled LLMs to achieve high accuracy on complex reasoning tasks by encouraging longer, more detailed reasoning chains. However, this often results in substantial response length inflation, with many tokens contributing little to actual problem-solving. The paper introduces Group Filtered Policy Optimization (GFPO), a method that addresses this inefficiency by sampling more candidate responses during training and filtering them based on desired attributes—primarily brevity and token efficiency—before applying policy optimization. The central claim is that increased training-time compute (via more sampling and filtering) can yield models that require less inference-time compute, producing concise yet accurate reasoning chains.

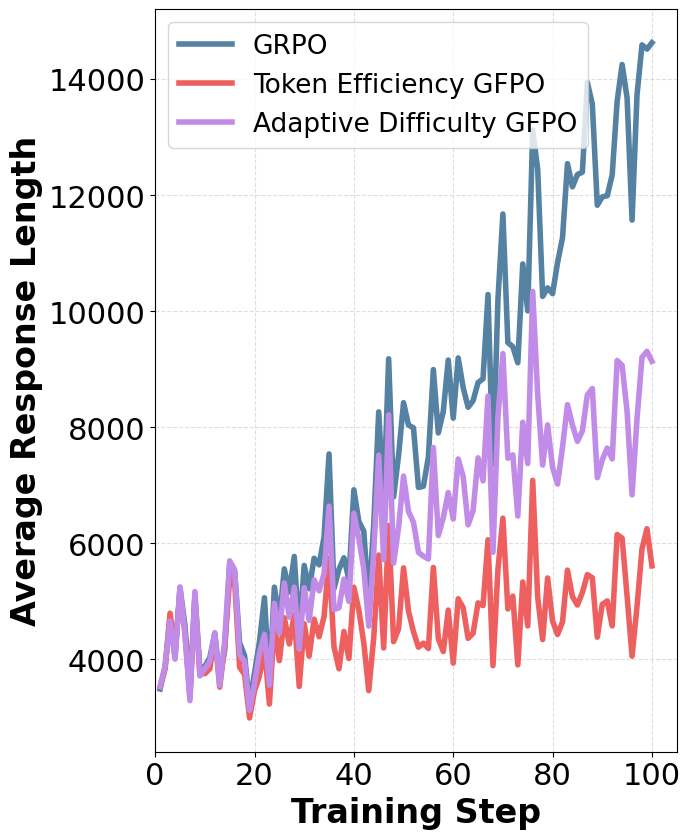
Figure 1: GFPO modifies GRPO by sampling more responses, ranking by a target attribute (e.g., length, token efficiency), and learning only from the top-k, thereby curbing length inflation while maintaining reasoning capabilities.

Methodology: GFPO and Its Variants

GFPO extends Group Relative Policy Optimization (GRPO) by introducing a selective learning step. For each training prompt, a group of $G$ candidate responses is sampled. These are then ranked according to a user-specified metric—response length or token efficiency (reward per token)—and only the top $k$ responses are used to compute policy gradients. The rest are masked out, receiving zero advantage. This approach serves as an implicit reward shaping mechanism, allowing the model to optimize for multiple attributes without complex reward engineering.

Three main GFPO variants are explored:

• Shortest $k/G$: Retain the $k$ shortest responses from $G$ samples.
• Token Efficiency: Retain the $k$ responses with the highest reward/length ratio.
• Adaptive Difficulty: Dynamically adjust $k$ based on real-time estimates of question difficulty, allocating more exploration to harder problems.

The GFPO objective is compatible with existing GRPO variants and loss normalization schemes (e.g., DAPO), and can be implemented with minimal changes to standard RLHF pipelines.

Experimental Setup

Experiments are conducted using the Phi-4-reasoning model, with RL training on 72k math problems and evaluation on AIME 24/25, GPQA, Omni-MATH, and LiveCodeBench. The baseline is GRPO with DAPO token-level loss normalization. GFPO is trained with increased group sizes ($G \in \{8, 16, 24\}$) and various $k$ values, always keeping $k \leq 8$ for fair comparison. Evaluation metrics include pass@1 accuracy, average response length, and excess length reduction (ELR).

Results: Length Reduction and Accuracy Preservation

GFPO achieves substantial reductions in response length inflation across all benchmarks, with no statistically significant loss in accuracy compared to GRPO. Key findings include:

• Length Reduction: Shortest 4/24 GFPO reduces length inflation by up to 59.8% on AIME 24, 57.3% on GPQA, and 71% on Omni-MATH. Token Efficiency GFPO achieves even larger reductions (up to 84.6% on AIME 24).
• Accuracy Preservation: Across all tasks, GFPO variants match GRPO's accuracy, as confirmed by Wilcoxon signed-rank tests.
• Pareto Superiority: For most benchmarks, at least one GFPO variant is strictly Pareto-superior to GRPO, achieving both higher accuracy and shorter responses.

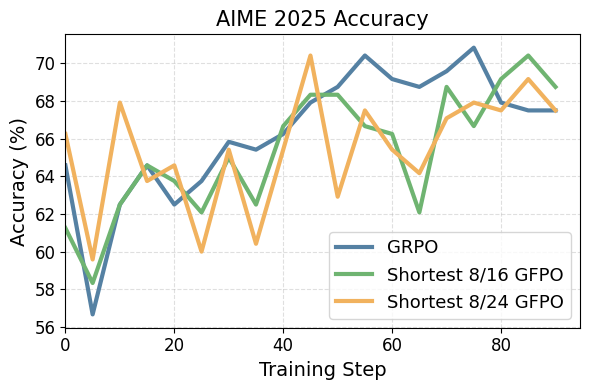
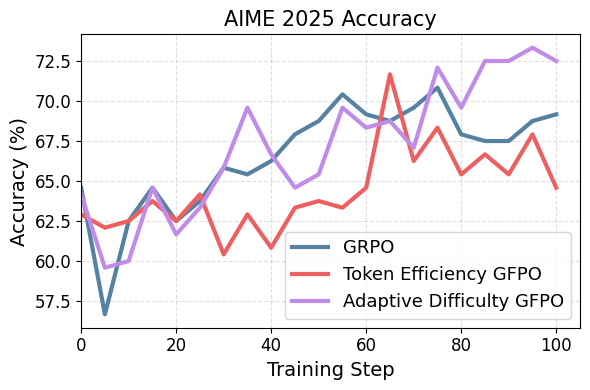
Figure 2: GFPO variants reach the same peak accuracy as GRPO on AIME 25 during training.

Figure 3: Pareto trade-off between accuracy and response length; GFPO variants dominate GRPO on most benchmarks.

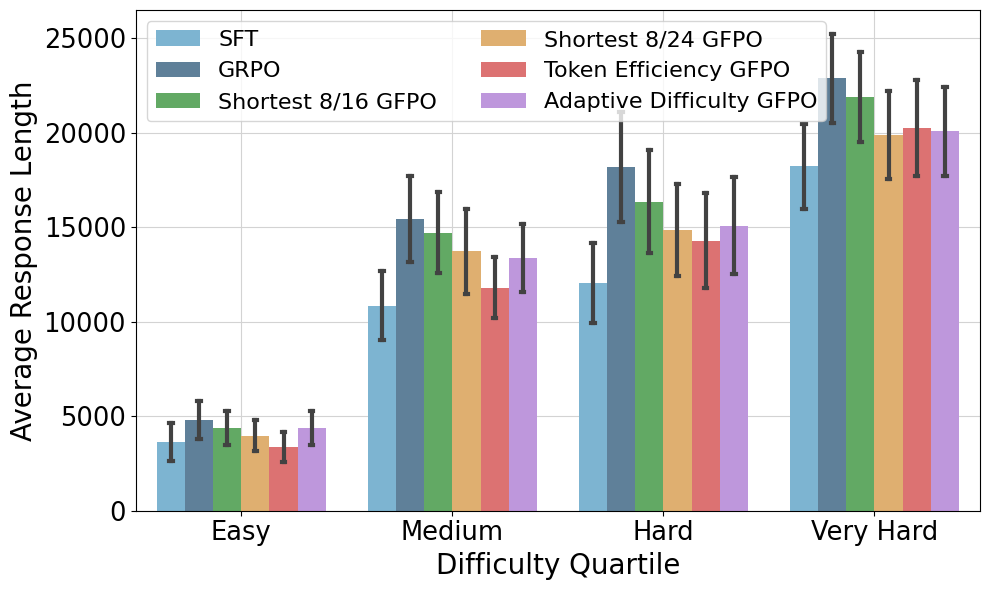
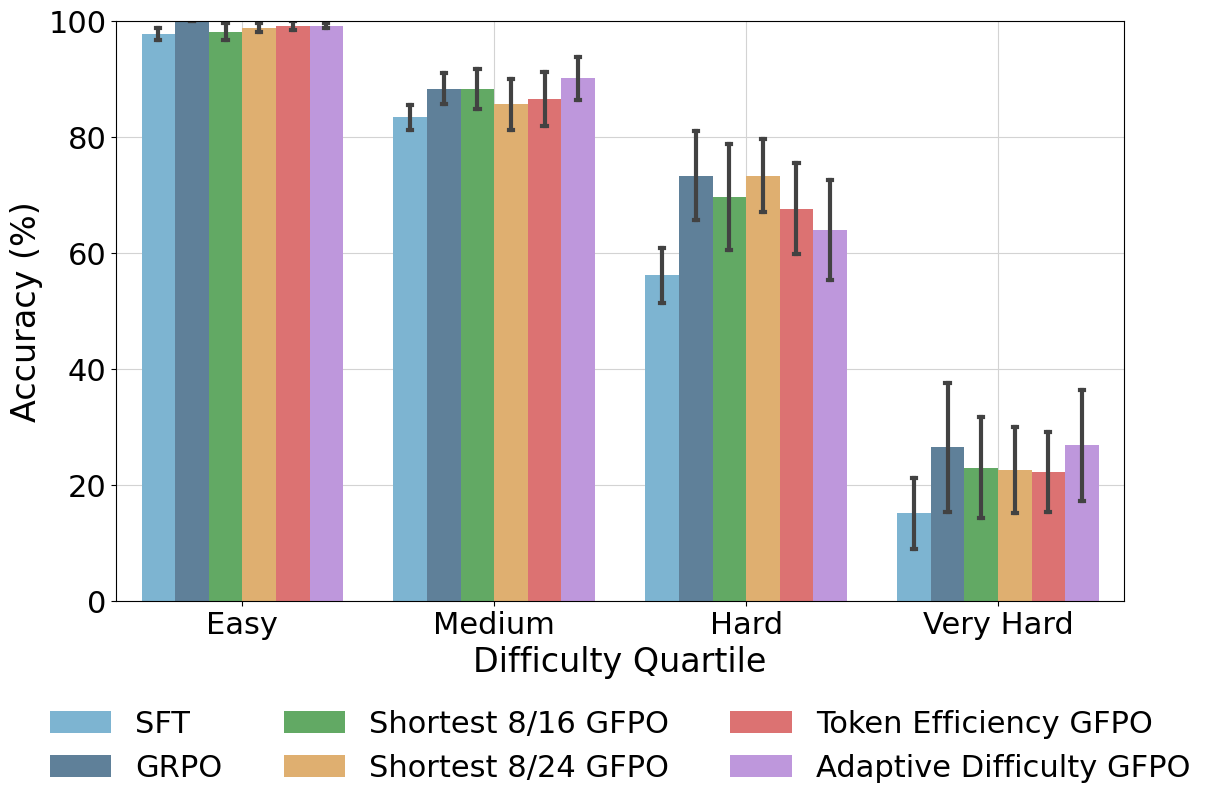
Analysis: Difficulty, Response Structure, and OOD Generalization

GFPO's impact is analyzed across problem difficulty levels and response structure:

• Difficulty Sensitivity: GFPO reduces verbosity across all difficulty levels. Token Efficiency GFPO achieves the largest reductions on easy and medium problems, while Shortest 8/24 is most effective on very hard problems.
• Accuracy-Length Relationship: Longer responses are less accurate even when controlling for problem difficulty. GFPO variants outperform GRPO in the longest response bins.
• Response Structure: GFPO primarily trims the Solution and Verification phases of reasoning traces, leaving the Problem and Final segments largely unchanged.

  Figure 4: Average response length increases with problem difficulty, but GFPO reduces excess length at all levels.

  

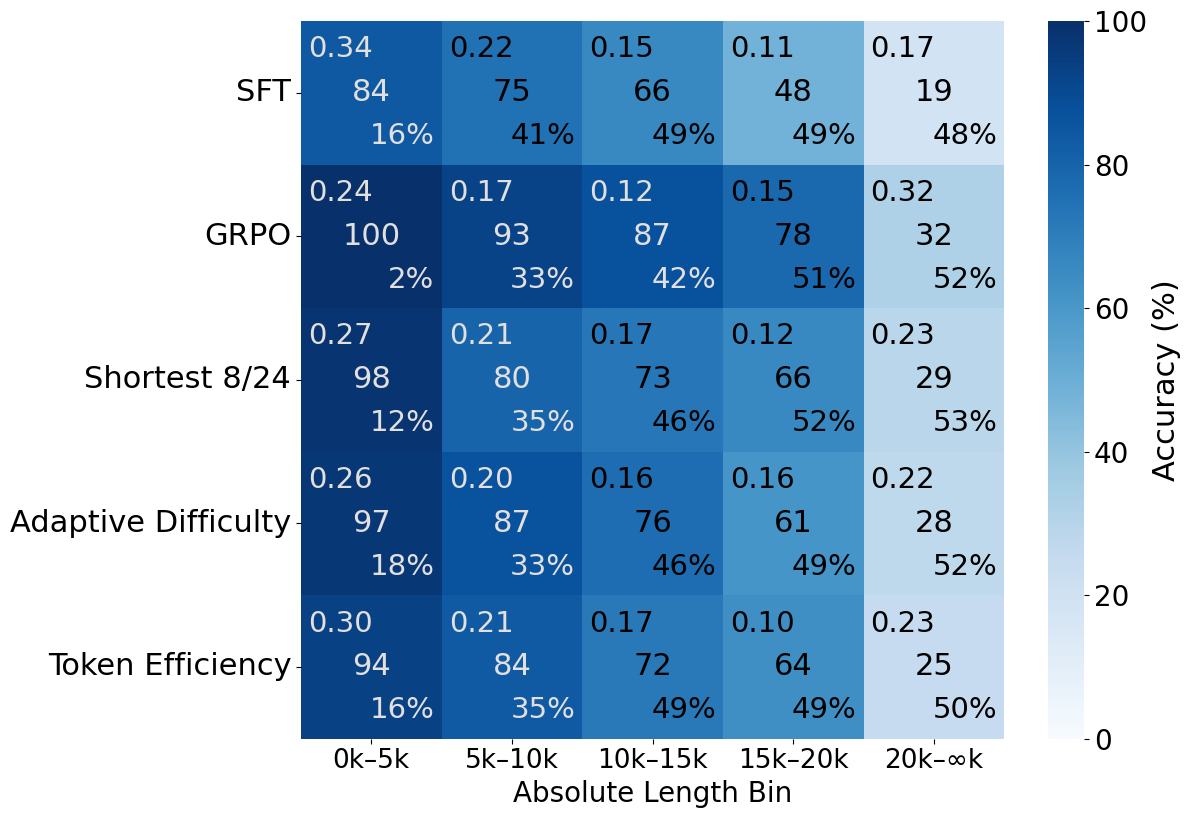
Figure 5: Adaptive Difficulty and Shortest 8/24 maintain the best accuracies across problem difficulties.

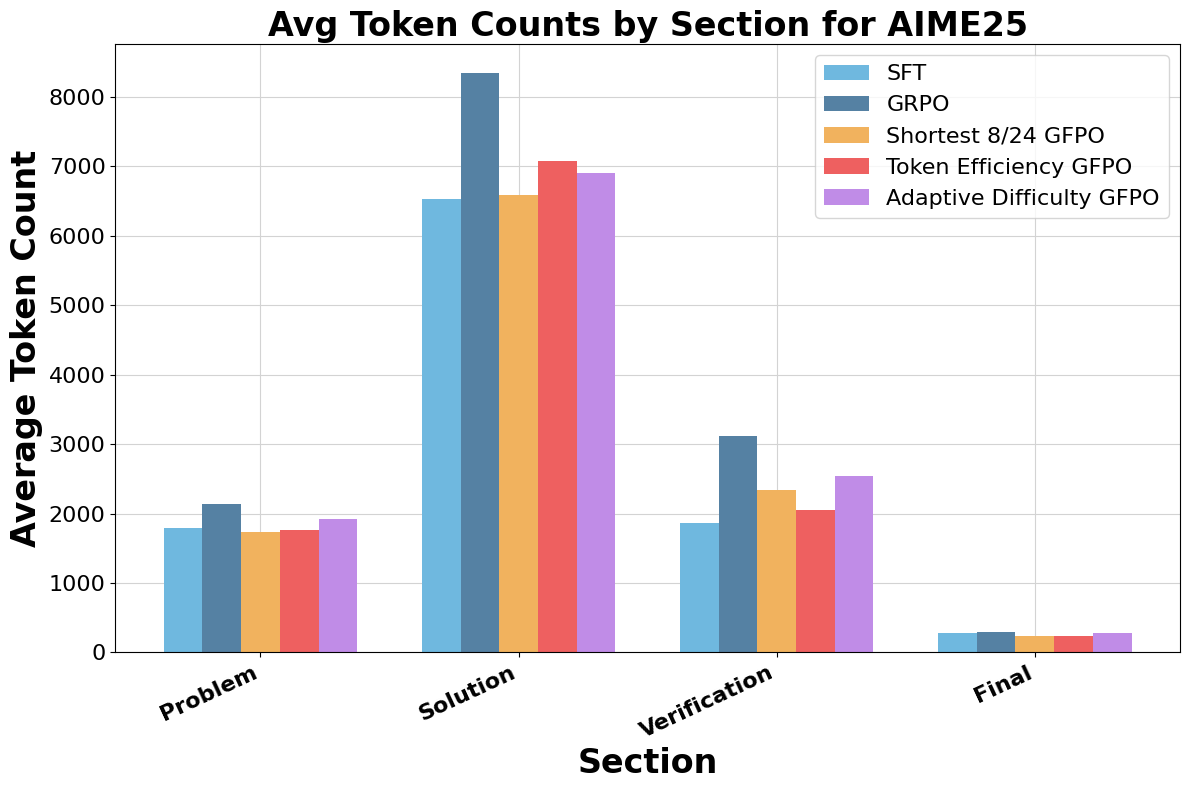
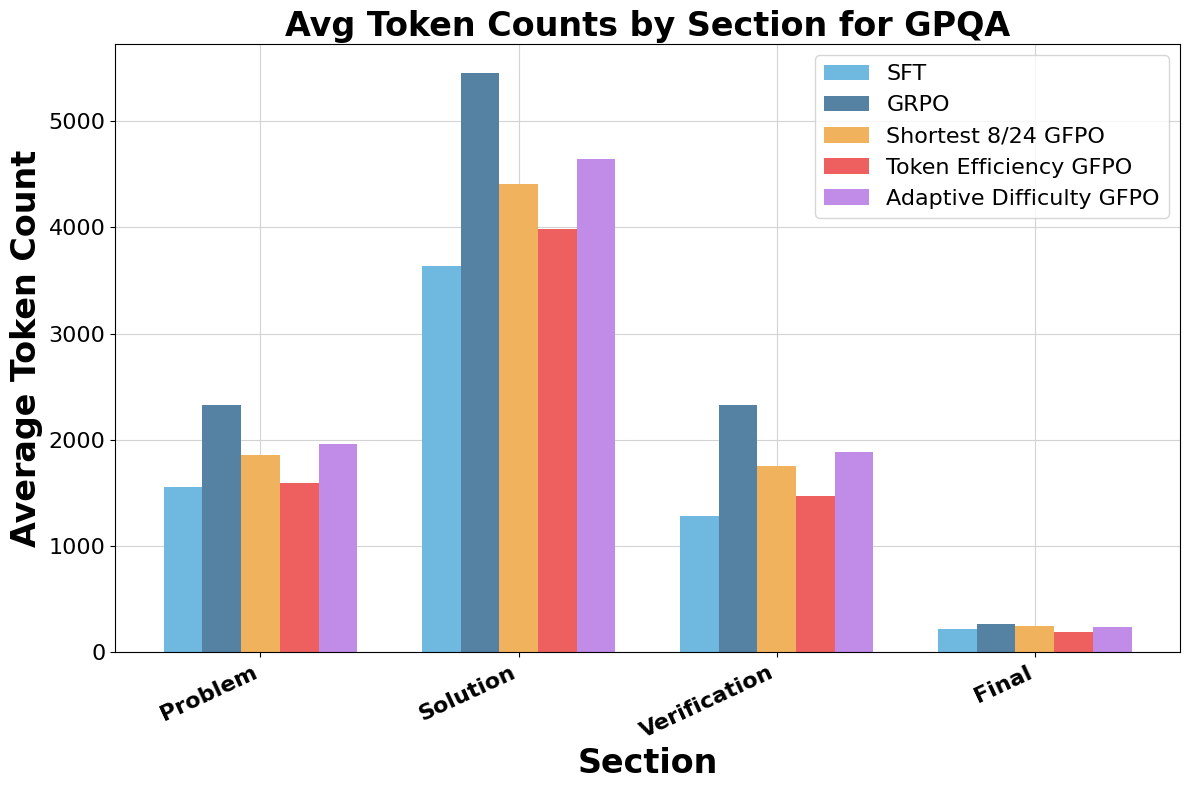
Figure 6: GFPO variants markedly reduce token counts in Solution and Verification phases compared to GRPO.

GFPO also generalizes well out-of-distribution: on LiveCodeBench (a coding benchmark not seen during RL training), GFPO curbs GRPO's length inflation and even yields modest accuracy improvements.

Implementation Considerations

GFPO is straightforward to implement in any RLHF pipeline supporting group-based policy optimization. The main computational cost is increased sampling during training, but this is offset by reduced inference-time compute due to shorter outputs. The method is agnostic to the specific reward function and can be combined with other RL loss normalization strategies. Adaptive Difficulty GFPO requires a lightweight streaming quantile estimator (e.g., t-digest) to track question difficulty.

Implications and Future Directions

GFPO demonstrates that selective learning via group filtering is an effective mechanism for controlling undesirable behaviors (e.g., verbosity) in RL-trained LLMs without sacrificing accuracy. The approach is general and can be extended to optimize for other attributes such as factuality, diversity, or safety. The trade-off between training-time and inference-time compute is particularly relevant for large-scale deployment, where inference costs dominate.

Potential future directions include:

• Integrating GFPO with more sophisticated reward models or multi-objective optimization.
• Applying GFPO to other domains (e.g., code generation, scientific reasoning) and modalities.
• Exploring hybrid approaches that combine GFPO with inference-time interventions for even tighter control over output properties.

Conclusion

Group Filtered Policy Optimization provides a principled and practical solution to the problem of response length inflation in RL-trained reasoning models. By sampling more and learning selectively, GFPO achieves substantial reductions in verbosity while preserving or even improving accuracy. The method is broadly applicable, computationally efficient at inference, and opens new avenues for fine-grained control over LLM behavior in high-stakes reasoning applications.