Position-Based Flocking for Robust Alignment (2508.04378v2)

Abstract: This paper presents a position-based flocking model for interacting agents, balancing cohesion-separation and alignment to achieve stable collective motion. The model modifies a position-velocity-based approach by approximating velocity differences using initial and current positions, introducing a threshold weight to ensure sustained alignment. Simulations with 50 agents in 2D demonstrate that the position-based model produces stronger alignment and more rigid and compact formations compared to the position-velocity-based model. The alignment metric and separation distances highlight the efficacy of the proposed model in achieving robust flocking behavior. The model's use of positions ensures robust alignment, with applications in robotics and collective dynamics.

• The paper presents a novel position-based flocking model that achieves robust velocity alignment and compact formations using only position information.
• The model employs finite differences of positions with a threshold weight to maintain long-term consensus, demonstrated by a rapid convergence of the alignment metric within 10 seconds.
• Simulations with 50 agents in 2D reveal rigid formations with lower separation distances, highlighting sensor robustness and reduced communication overhead in multi-agent systems.

Position-Based Flocking for Robust Alignment: Model, Analysis, and Implications

Introduction

The paper "Position-Based Flocking for Robust Alignment" (2508.04378) introduces a novel position-based flocking model for multi-agent systems (MAS), emphasizing robust velocity alignment and compact formation using only position data. The work addresses the limitations of velocity-dependent flocking algorithms, which are often impractical in robotic applications due to sensor noise and communication constraints. By leveraging initial and current positions, the proposed model achieves strong alignment and rigid formations, outperforming traditional position-velocity-based approaches in both simulation and theoretical analysis.

Model Formulation

The classical flocking paradigm is governed by three principles: cohesion, separation, and alignment. The position-velocity-based model, as formalized in prior work, utilizes both position and velocity states for agent interactions. The dynamics for agent $i$ are:

$$\frac{d\mathbf{p}_i}{dt} = \mathbf{v}_i, \quad \frac{d\mathbf{v}_i}{dt} = \sum_{j \in \mathcal{N}_i} \psi(\|\mathbf{p}_j - \mathbf{p}_i\|)(\mathbf{p}_j - \mathbf{p}_i) + \sum_{j \in \mathcal{N}_i} \phi (\mathbf{v}_j - \mathbf{v}_i)$$

where $\psi$ and $\phi$ are interaction weights, and $\mathcal{N}_i$ is the neighborhood of agent $i$.

The position-based model modifies the alignment term by approximating velocity differences using finite differences of positions:

$$\mathbf{v}_j - \mathbf{v}_i \approx \frac{(\mathbf{p}_j - \mathbf{p}_i) - (\mathbf{p}_j(0) - \mathbf{p}_i(0))}{t}$$

To prevent the alignment influence from vanishing as $t \to \infty$, a threshold weight $\hat{\phi}_{\text{min}} = k |\mathcal{N}_i|$ is introduced, yielding the alignment term:

$$\sum_{j \in \mathcal{N}_i} \max\left( \frac{|\mathcal{N}_i|}{t}, \hat{\phi}_{\text{min}} \right) \left[ (\mathbf{p}_j - \mathbf{p}_i) - (\mathbf{p}_j(0) - \mathbf{p}_i(0)) \right]$$

The full position-based flocking dynamics are:

$$\frac{d\mathbf{p}_i}{dt} = \mathbf{v}_i, \quad \frac{d\mathbf{v}_i}{dt} = \sum_{j \in \mathcal{N}_i} \hat{\psi}(\|\mathbf{p}_j - \mathbf{p}_i\|)(\mathbf{p}_j - \mathbf{p}_i) + \sum_{j \in \mathcal{N}_i} \hat{\phi}(\mathbf{p}_j(0) - \mathbf{p}_i(0))$$

where $\hat{\psi}$ and $\hat{\phi}$ are modified weights incorporating the threshold.

Simulation Results and Comparative Analysis

Simulations with $n=50$ agents in 2D space demonstrate the efficacy of the position-based model. Agents are initialized with random positions and velocities, and the interaction radius is set to $r_i = 7.5$ m. The alignment metric $\gamma$ is used to quantify directional consensus, defined as the average cosine similarity of velocity vectors among neighbors.

Snapshots of the position-velocity-based model reveal partial alignment and flexible formations, with alignment peaking mid-simulation and declining in the final state.

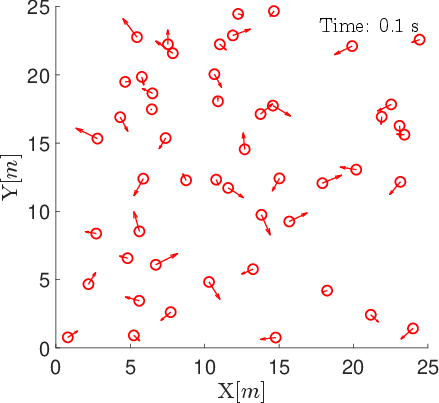
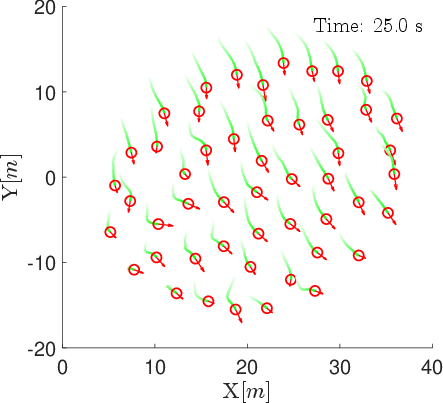
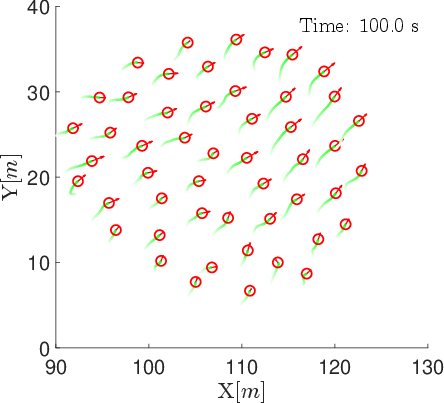
Figure 1: Snapshots of agent positions and velocity vectors under the position-velocity-based model at $t=0, 25, 50, 75, 100$ s.

Time histories for this model show transient strong alignment ($\gamma \approx 1$) followed by a decrease, and separation distances remain relatively wide.

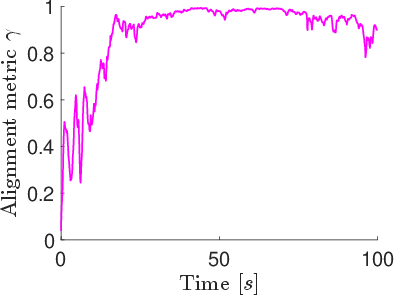
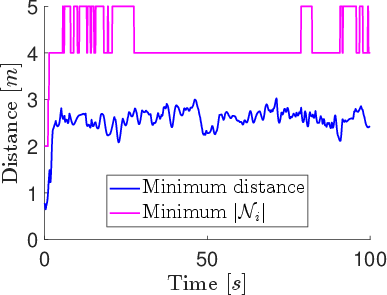
Figure 2: Alignment metric $\gamma$ and minimum separation distance over time for the position-velocity-based model.

In contrast, the position-based model achieves rapid and sustained strong alignment, with $\gamma$ converging to near 1 within 10 s and remaining stable. Formations are rigid and compact, with minimum separation distances consistently lower (1.5–2 m).

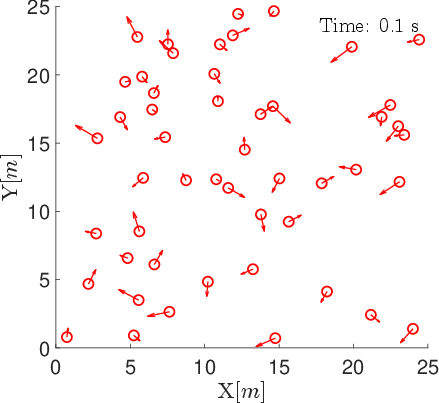
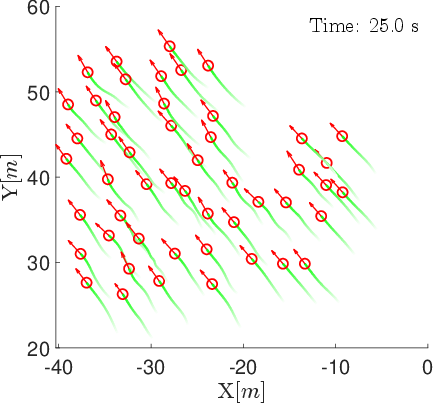
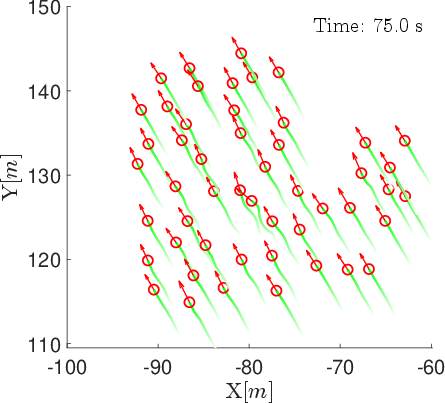
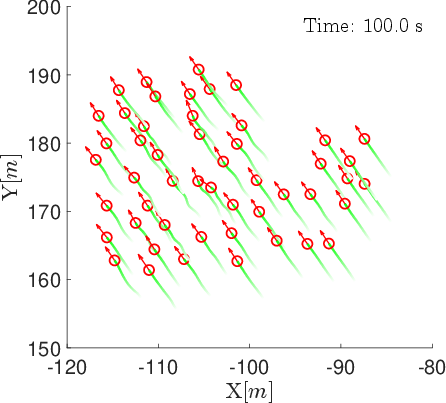
Figure 3: Snapshots of agent positions and velocity vectors under the position-based model at $t=0, 25, 50, 75, 100$ s.

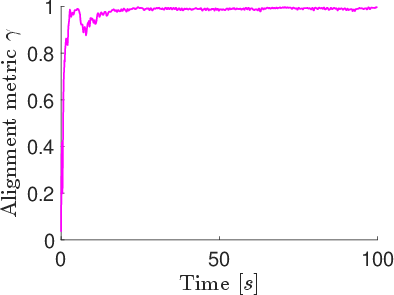
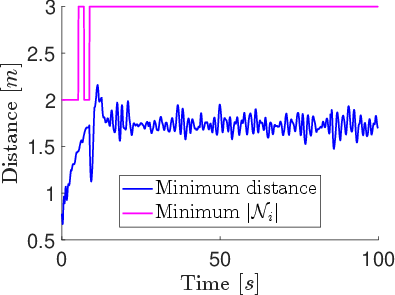
Figure 4: Alignment metric $\gamma$ and minimum separation distance over time for the position-based model.

Ablation experiments without the threshold weight ($\hat{\phi} = |\mathcal{N}_i|/t$) show initial strong alignment, but $\gamma$ declines as $t$ increases, confirming the necessity of the threshold for sustained consensus.

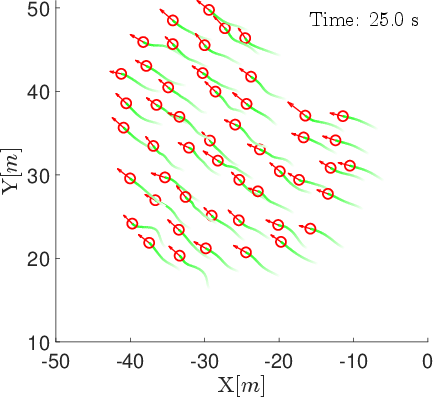
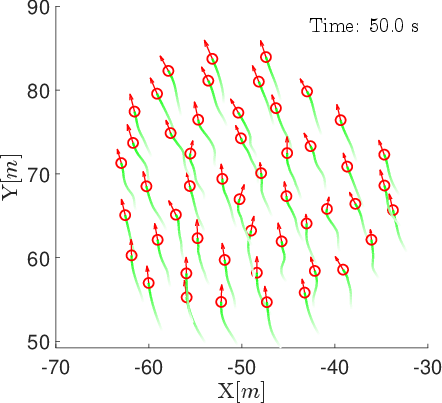
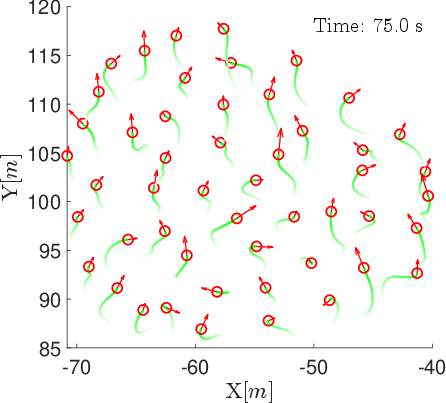
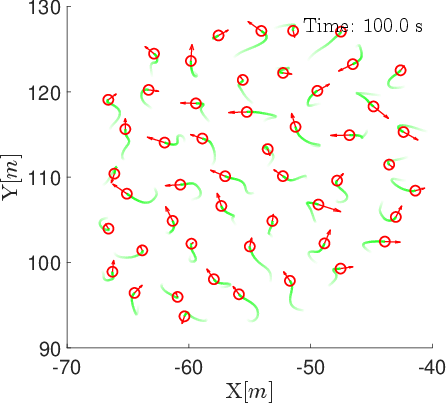
Figure 5: Snapshots of agent positions and velocity vectors under the position-based model without threshold weight at $t=0, 25, 50, 75, 100$ s.

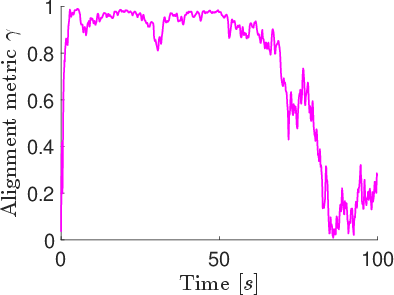
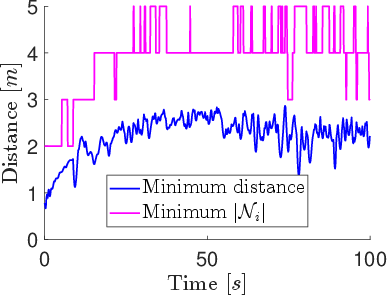
Figure 6: Alignment metric $\gamma$ and minimum separation distance over time for the position-based model without threshold weight.

The comparative summary highlights the following:

Characteristic	Pos-Vel-Based	Position-Based
Alignment	Strong	Very strong
Formation	Flexible	Rigid
Separation	Wider	Narrower

Practical and Theoretical Implications

The position-based model offers several advantages for MAS, particularly in robotics:

• Sensor Robustness: Relies solely on position measurements, which are less susceptible to noise and easier to obtain (e.g., via GPS, LIDAR).
• Reduced Communication: Halves communication bandwidth requirements by eliminating velocity data exchange.
• Scalability: Distributed and density-adaptive weighting enables operation in large-scale swarms.
• Fault Tolerance: Utilizes last-known positions, enhancing resilience to intermittent communication or sensor failures.
• Formation Control: Achieves more compact and rigid formations, beneficial for applications requiring precise spatial arrangements (e.g., drone swarms, automated vehicles).

Theoretically, the model demonstrates that robust velocity consensus and spatial cohesion can be achieved without explicit velocity measurements, provided that initial and current positions are available and the alignment weight is properly regulated. The threshold mechanism is essential to prevent the decay of alignment influence, ensuring long-term stability.

Future Directions

Potential extensions include:

• Adaptive Interaction Radii: Dynamically adjusting $r_i$ based on local density or task requirements.
• Noise Robustness: Incorporating stochastic position measurements and analyzing convergence under uncertainty.
• Dynamic Thresholds: Modulating $\hat{\phi}_{\text{min}}$ in response to environmental changes or agent failures.
• 3D Formations: Extending the model to three-dimensional spaces and heterogeneous agent capabilities.
• Hardware Implementation: Deploying the algorithm on real robotic platforms to validate performance under practical constraints.

Conclusion

The position-based flocking model presented in this work achieves robust alignment and compact formations using only position data, with a threshold weight ensuring sustained velocity consensus. Simulation results confirm superior performance over position-velocity-based models, with implications for scalable, resilient, and efficient multi-agent coordination in robotics and collective dynamics. The approach provides a foundation for further research into adaptive, noise-tolerant, and hardware-friendly flocking algorithms.