Hidden Dynamics of Massive Activations in Transformer Training (2508.03616v1)

Abstract: Massive activations are scalar values in transformer hidden states that achieve values orders of magnitude larger than typical activations and have been shown to be critical for model functionality. While prior work has characterized these phenomena in fully trained models, the temporal dynamics of their emergence during training remain poorly understood. We present the first comprehensive analysis of massive activation development throughout transformer training, using the Pythia model family as our testbed. Through systematic analysis of various model sizes across multiple training checkpoints, we demonstrate that massive activation emergence follows predictable mathematical patterns that can be accurately modeled using an exponentially-modulated logarithmic function with five key parameters. We develop a machine learning framework to predict these mathematical parameters from architectural specifications alone, achieving high accuracy for steady-state behavior and moderate accuracy for emergence timing and magnitude. These findings enable architects to predict and potentially control key aspects of massive activation emergence through design choices, with significant implications for model stability, training cycle length, interpretability, and optimization. Our findings demonstrate that the emergence of massive activations is governed by model design and can be anticipated, and potentially controlled, before training begins.

• The paper presents a mathematical model that captures the evolution of massive activations in transformers across various layers and model sizes.
• It demonstrates that activation patterns differ by layer depth, with early peaks in shallow/deep layers and logarithmic increases in middle layers.
• It proposes a machine learning framework that predicts and controls activation dynamics by leveraging key architectural features like attention density.

Hidden Dynamics of Massive Activations in Transformer Training

Introduction

The paper "Hidden Dynamics of Massive Activations in Transformer Training" presents a comprehensive analysis of the emergence and evolution of massive activations (MAs) in transformer models during training. Massive activations are defined as scalar values in transformer hidden states that are orders of magnitude larger than typical activations. These activations have significant implications for model functionality, stability, and optimization. The paper uses the Pythia model family as a testbed to systematically analyze the development of MAs across various model sizes and training checkpoints.

Mathematical Modeling of Massive Activations

The authors introduce a mathematical framework to model the emergence of MAs using an exponentially-modulated logarithmic function with five key parameters: amplitude ($A$), decay rate ($\lambda$), time scaling ($\gamma$), time offset ($t_0$), and asymptotic baseline ($K$). This model accurately captures the temporal dynamics of MAs across different layers and model sizes.

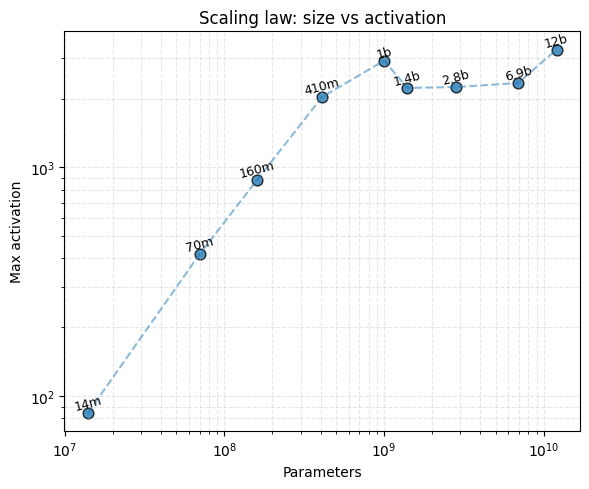
Figure 1: Plot of transformer parameter count vs value of the top activation to median ratio per model, in each respective final model checkpoint.

Evolution of Massive Activations

The paper reveals that MAs are learned throughout training and exhibit distinct patterns depending on layer depth. Shallow and deep layers tend to show an early peak in MA magnitude, followed by a decay, while middle layers display a logarithmic increase without a clear peak during the training window.

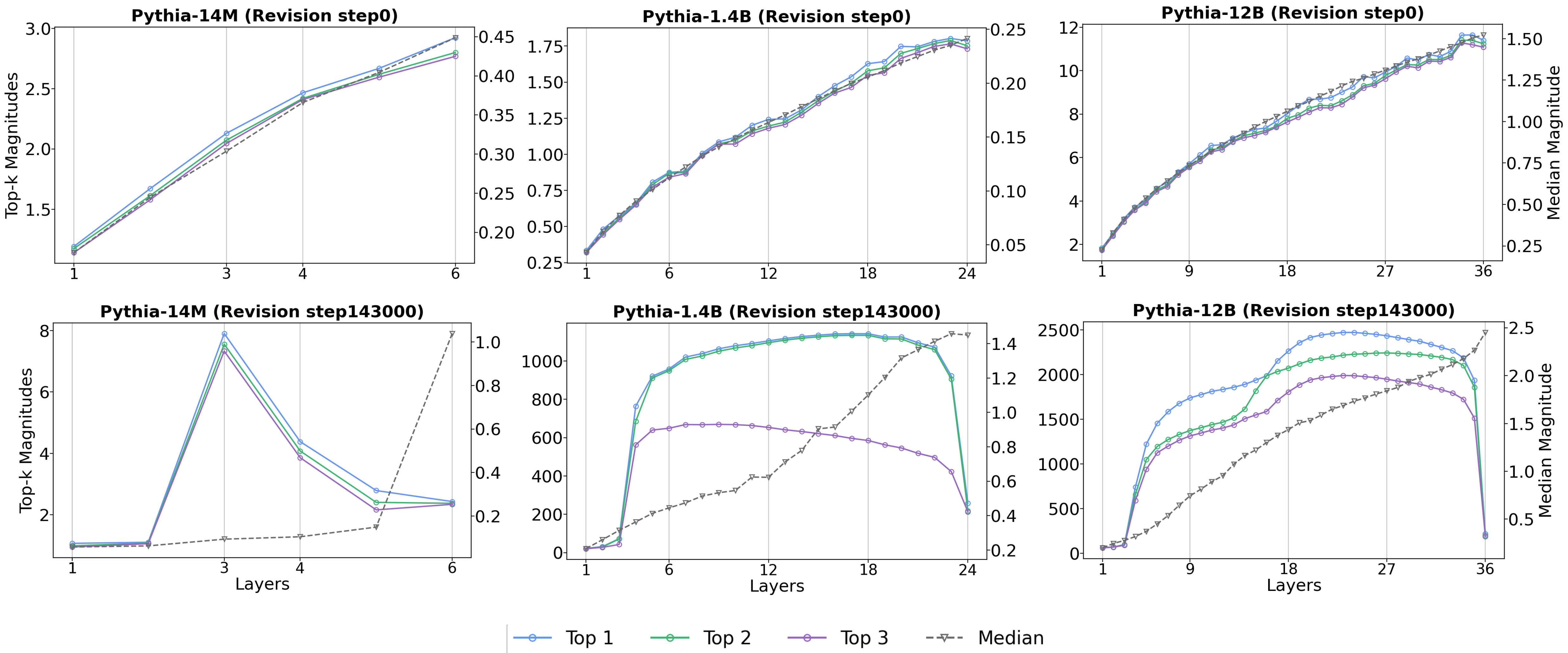
Figure 2: Top activation magnitudes per layer in models Pythia-14M, Pythia-1.4B, and Pythia-12B at revision step 0 and 143000, which correspond to the start and end of training.

The authors fit the MA trajectories with the proposed mathematical model, achieving a high average coefficient of determination ($R^2 = 0.984$), indicating strong predictability of MA dynamics.

Predicting Massive Activation Trajectories

The paper develops a machine learning framework to predict the parameters of the MA model from architectural specifications alone. The framework uses features such as layer position, attention density, and model width/depth ratio to predict the emergence and steady-state behavior of MAs.

Figure 3: Evolution of the ratio of top activations to median during training for Pythia 1B.

The analysis shows that attention density and layer position are the dominant drivers of MA emergence and amplitude. By adjusting these architectural features, model designers can control the timing and magnitude of MAs.

Implications and Future Directions

The findings demonstrate that MAs are not random artifacts but follow systematic, architecture-dependent rules. This understanding allows for MA-aware architecture design, enabling practitioners to predict and control MA dynamics through design choices. The paper opens avenues for further research into the relationship between MA dynamics and training efficiency, as well as the generalization of these findings to other model families and architectures.

Conclusion

The paper provides a quantitative, predictive, and interpretable model of MA emergence in transformers, with significant implications for model design and optimization. By establishing a framework for understanding and controlling MAs, the paper offers a foundation for future research and development in transformer architectures.