Modeling Loss-Versus-Rebalancing in Automated Market Makers via Continuous-Installment Options (2508.02971v1)

Abstract: This paper mathematically models a constant-function automated market maker (CFAMM) position as a portfolio of exotic options, known as perpetual American continuous-instaLLMent (CI) options. This model replicates an AMM position's delta at each point in time over an infinite time horizon, thus taking into account the perpetual nature and optionality to withdraw of liquidity provision. This framework yields two key theoretical results: (a) It proves that the AMM's adverse-selection cost, loss-versus-rebalancing (LVR), is analytically identical to the continuous funding fees (the time value decay or theta) earned by the at-the-money CI option embedded in the replicating portfolio. (b) A special case of this model derives an AMM liquidity position's delta profile and boundaries that suffer approximately constant LVR, up to a bounded residual error, over an arbitrarily long forward window. Finally, the paper describes how the constant volatility parameter required by the perpetual option can be calibrated from the term structure of implied volatilities and estimates the errors for both implied volatility calibration and LVR residual error. Thus, this work provides a practical framework enabling liquidity providers to choose an AMM liquidity profile and price boundaries for an arbitrarily long, forward-looking time window where they can expect an approximately constant, price-independent LVR. The results establish a rigorous option-theoretic interpretation of AMMs and their LVR, and provide actionable guidance for liquidity providers in estimating future adverse-selection costs and optimizing position parameters.

• The paper introduces a rigorous option-theoretic framework equating AMM loss-versus-rebalancing costs to continuous-installment put option funding fees.
• The paper models CFAMM positions as a portfolio of perpetual CI put options, demonstrating that discrete replication closely matches the AMM delta profile with bounded error.
• The paper provides actionable design rules for liquidity providers to optimize liquidity bands and holding periods using market-implied volatility data.

Modeling Loss-Versus-Rebalancing in Automated Market Makers via Continuous-InstaLLMent Options

Introduction and Motivation

This paper develops a rigorous option-theoretic framework for modeling the loss-versus-rebalancing (LVR) cost incurred by liquidity providers (LPs) in constant-function automated market makers (CFAMMs), such as Uniswap v2/v3. The central contribution is the identification of a mathematical equivalence between the LVR of a CFAMM position and the funding fees of a portfolio of perpetual American continuous-instaLLMent (CI) put options. This equivalence enables forward-looking, closed-form estimation of LVR, and provides actionable design rules for LPs to select liquidity bands and holding periods with predictable, price-path-independent adverse selection costs.

The motivation arises from the persistent value transfer from LPs to arbitrageurs due to the lag between AMM prices and primary market prices. While prior work has quantified instantaneous and historical LVR, this paper addresses the forward estimation problem, leveraging the time-invariant properties of perpetual CI options to construct static, delta-replicating portfolios for AMM positions.

Option-Theoretic Decomposition of CFAMM Positions

The paper models a concentrated CFAMM position as a portfolio of perpetual American CI put options, each with a different strike, and with funding rates tending to infinity. In this limit, the exercise and abandonment boundaries of each CI put collapse to the strike, and the option's delta becomes a step function. This property allows the construction of a portfolio that exactly matches the delta profile of any smooth CFAMM value function.

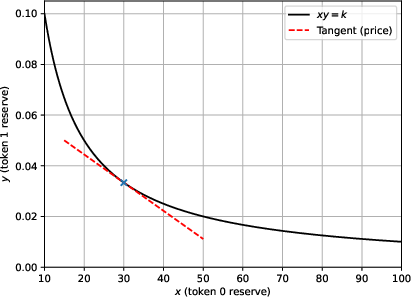
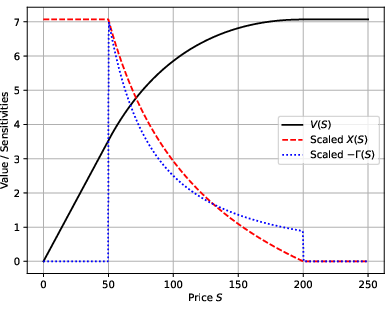
Figure 1: CPAMM invariant with $k=1$ and marginal price, illustrating the geometric structure of the AMM reserve curve.

The key result is that the instantaneous LVR of the AMM position is analytically identical to the funding fee (theta) of the at-the-money CI option in the replicating portfolio. This is formalized by constructing a continuous (or, in practice, discrete) strip of CI puts, weighted by the second derivative of the AMM value function with respect to price. The funding fee received by the option seller, in the limit of large funding rates, converges to the LVR cost experienced by the LP.

Analytical Results: LVR as CI Funding Fees

The equivalence between LVR and CI funding fees is established via a sequence of lemmas and theorems. For a discrete portfolio of CI puts with finite funding rates, the total funding fee at any time is dominated by the option whose continuation region contains the spot price. As the funding rate increases, the width of the continuation region shrinks, and the funding fee converges to the instantaneous LVR:

$$\lim_{q \to \infty} w_j q = \frac{\sigma^2 S^2}{2} X'(S)$$

where $w_j$ is the weight of the active option, $q$ is the funding rate, $\sigma$ is volatility, $S$ is spot price, and $X'(S)$ is the gamma of the AMM position.

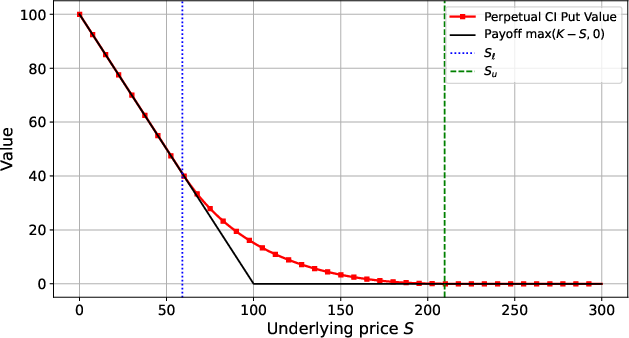
Figure 2: Discounted value of a perpetual CI put option with lower and upper boundaries, showing the exercise and abandonment regions.

A further result shows that if the AMM liquidity band is chosen to match the delta of a single CI put, the LVR becomes nearly constant and equal to the funding rate $q$, up to a bounded residual error. This enables LPs to design positions with predictable, price-path-independent LVR over arbitrarily long forward windows.

Error Analysis of Discrete CI Option Replication

In practice, a continuous strip of options is infeasible; the paper quantifies the error introduced by discretizing the strike space and using finite funding rates. The error metrics considered are the maximum absolute error and root-mean-square error (RMSE) between the target AMM delta and the delta of the discrete CI put strip.

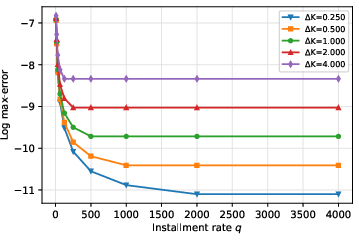
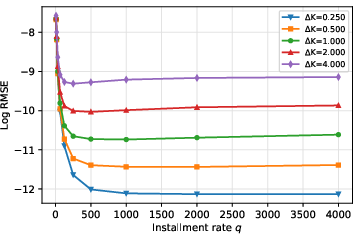
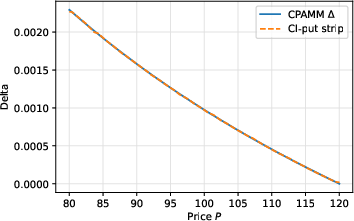
Figure 3: Log max error in delta replication as a function of funding rate $q$ and strike spacing $\Delta K$.

The results demonstrate that both errors decrease as the funding rate increases and the strike spacing decreases. For practical purposes, a small number of CI puts with sufficiently large $q$ can replicate the AMM delta within tight error bounds, making the approach implementable for LPs seeking to immunize against LVR.

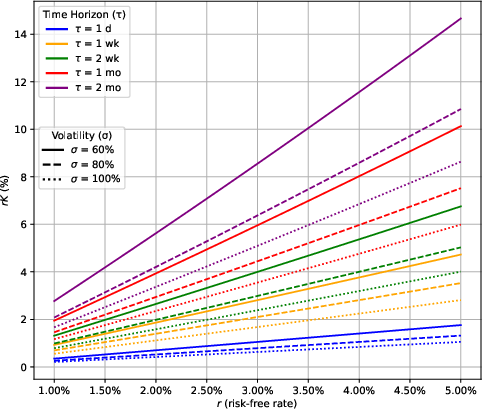
Volatility Calibration and Effective Time Horizon

A critical implementation detail is the calibration of the constant volatility parameter required for perpetual CI put pricing. Since market data provides a term structure of implied volatilities (IVs) for fixed maturities, the paper derives a mapping from the CI put's expected first-exit time (the mean time until the spot price leaves the continuation band) to an effective implied volatility.

Figure 4: Distribution of first-exit time $\tau$ for a CI put, quantifying the expected holding period as a function of band width and volatility.

The effective squared volatility is estimated by interpolating total variances from market IVs at the relevant time horizon. The paper provides error bounds for this approximation, showing that the error is small when the IV curve is flat (as is typical for long maturities), and quantifies the mean absolute deviation and RMSE.

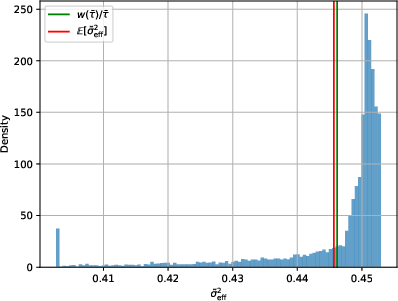
Figure 5: Distribution of $\sigma^2$ for $r=2\%$, $\sigma=61\%$, $K=100$, $q=5$ using ETH ATM IVs, illustrating the calibration of effective volatility.

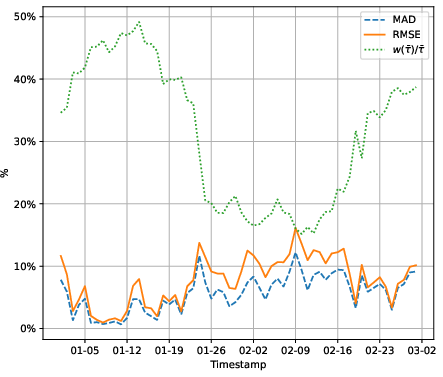
Figure 6: MAD and RMSE for $r=5\%$, $K=100$, $q=40$, where $\sigma_\mathrm{eff}^2$ is derived by fixed point methods, showing the tightness of the volatility estimation.

Practical Implications for Liquidity Providers

The framework enables LPs to:

• Select liquidity bands and holding periods that yield predictable, fixed LVR costs, facilitating direct comparison with expected trading fee income.
• Estimate forward-looking LVR using observable option market data, rather than relying on historical or instantaneous volatility.
• Construct discrete CI put portfolios to statically hedge AMM positions, reducing the need for frequent rebalancing.
• Calibrate position parameters (band width, shape, holding period) to market-implied volatility surfaces, optimizing for desired risk and return profiles.

  Figure 7: Residual upper bound $rK$ as a percentage of $q$ for various time horizons and $\sigma_\mathrm{eff}$ exposures, quantifying the bounded error in LVR estimation.

The analysis also highlights the trade-off between capital efficiency (narrow bands, high $q$) and operational complexity (finer strike meshes), and provides explicit design tables for various volatility and time horizon scenarios.

Theoretical and Future Directions

The paper's results establish a closed-form, time-invariant correspondence between AMM LVR and CI option funding fees, providing a new lens for understanding adverse selection in DeFi markets. The approach is robust to the choice of AMM invariant and can be extended to more general liquidity profiles.

Future research directions include:

• Extending the analysis to asymmetric liquidity bands and off-ATM positions, requiring integration over the full volatility surface.
• Incorporating stochastic or time-dependent volatility models (e.g., Heston, Hull-White) to capture more realistic market dynamics.
• Quantifying the impact of transaction costs, slippage, and discrete trading on the LVR–CI equivalence.
• Exploring the development of on-chain CI option markets as direct hedging instruments for LPs.

Conclusion

This work provides a rigorous, actionable framework for modeling and managing LVR in AMMs via a novel decomposition into perpetual American CI put options. The analytical equivalence between LVR and CI funding fees enables forward-looking, predictable estimation of adverse selection costs, and offers practical tools for LPs to optimize position parameters using observable market data. The discrete error analysis confirms the feasibility of implementation, and the volatility calibration procedure bridges the gap between perpetual option theory and real-world IV surfaces. The framework opens new avenues for both theoretical exploration and practical risk management in DeFi liquidity provision.